基于ARIMA的煤炭产业政策有效性评估方法
2018-11-20汪文生孙小波
汪文生,张 蓉,孙小波,刘 颖
(1.中国矿业大学(北京)管理学院,北京 100083;2.煤炭资源与安全开采国家重点实验室,北京 100083)
国家宏观管理部门一直高度关注煤炭产业运行发展态势,适时出台了一系列宏观调控政策。判断产业调控政策的有效性是改进宏观调控方式方法,促进产业健康可持续发展的重要基础[1]。然而,国内外对我国煤炭产业政策实施有效性评估的研究十分匮乏[2]。
实证主义的政策评估方法中使用较多的是社会实验法[3]。社会实验的基本思想就是随机把评估对象分为两组,一组为实验组,一组是控制组。只对实验组实施政策,然后将两组的结果进行对比,来检验政策的实施效果。如果通过对比发现只有实验组有变化,那么两组的差异就是政策干预所致。这种方法被视为最有效的社会实验方法——随机控制试验。但是在现实的政策评估中很难选取控制组或是随机分配控制组,大家通常会采用准实验法:就是将控制组替换成和实验组相似度较高的组。准实验法在政策干预和评估对象存在非常密切的关系,而且评估对象所处外界环境比较稳定时可靠性较高。由于煤炭产业调控政策的有效性受多种因素影响,而且产业政策覆盖面比较全面(多为全国性政策),很难建立实验组和控制组,所以随机控制实验法和准实验法不可行[4]。基于社会实验法存在的困难,考虑到很多煤炭产业调控政策都是针对煤炭价格或期望通过煤炭价格变动达到预期调控目的,本文提出一种基于ARIMA煤炭价格预测模型的“投射-实施后”对比分析评估法,通过对比政策实施前后的价格差异,对政策实施效果进行评估[5-6]。
1 基本原理
“投射”是指根据政策执行前的各种情况建立一个煤炭价格趋势倾向线,并将这个趋向线外推到政策执行后的某一点A1,代表若无该政策会发生的情况;设A2为政策“实施后”的实际情况,通过将A1点与A2点对比,可以估计产业政策的效果。
煤炭价格趋势倾向线可以通过建立自回归移动平均模型(auto-regressive integrated moving average model,简记ARIMA)得到。ARIMA模型的基本思想是:将经济时间序列数据看作是一个随机序列,这个序列随时间的推移生成不同随机的数据,这些数据本身存在一定的内在规律或者结构。本文以时间序列的自相关分析为基础,通过数学理论模型构造其演变结构,近似地来描述这个序列[7]。这个模型被发现之后,可以通过将经济时间数据的历史值输入模型,输出经济时间序列的未来值,实现预测功能[8]。ARIMA模型在构造时,既考虑了经济时间序列数据本身的前后相关性,也对实际经济时间序列数据可能受到的干扰因素加以分析,因此该模型与实际经济现象的契合度比较高,可以很好的应用于构建煤炭价格趋势倾向线[9]。
一般而言,煤炭价格时间序列数据可能是非平稳的,本文建立ARIMA(p,d,q)差分自回归移动平均模型。其中:p为自回归项,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。ARIMA模型预测有两种方式,分别是静态预测与动态预测。静态预测是指预测值是基于上期(滞后期)的实际值,而动态预测是基于上期(滞后期)的拟合值。确定三个参数值的过程,就是模型的识别过程。首先对原始数据进行平稳性检验,如果原始时间序列数据是平稳的,则d=0;否则要对原始数据做一阶差分处理,使差分后的数列具有平稳性,此时d=1;一阶差分后的序列依然不平稳就要进行二阶差分处理,一般的经济变量二阶差分之后都会变成平稳序列,此时d=2。p和q可通过自相关和偏自相关分析得到[10]。
2 ARIMA模型构建
2.1 数据来源
在煤炭价格数据选择时,鉴于秦皇岛港是我国现在最大的煤炭交易市场,从这个港口交易的煤炭量占比达到全国港口的40%以上。北方大部分产煤大省的煤炭主要是通过秦皇岛港运往南方各城市,保障南方的煤炭供应。所以选择秦皇岛港的煤炭价格数据具有很强的代表性,直接反映了我国煤炭市场价格的整体趋势。煤炭价格数据来自中国煤炭市场网,选取2000~2016年秦皇岛大同优混(发热量为6 000大卡[注]1大卡=1千卡(kcal)=4.84千焦(kJ))平仓价格代表中国煤炭价格(图1),并对所取得的价格区间取平均值得到中国煤炭价格月度数据。
2.2 单位根检验
首先对原序列进行检验,结果见表1。统计量t值大于各显著性水平下的临界值,接受原假设,原序列有一个单位根,即原序列是非平稳序列。
对原数据一阶差分后进行单位根检验,结果见表2。统计量t值小于1%显著性水平下的临界值,拒绝原假设,序列差分后没有单位根,差分后序列平稳。

图1 秦皇岛大同优混(6 000大卡)平仓价格走势
表1 原序列单位根检验结果

增广迪基-福勒检验统计量T-统计量概率-0.1755260.6215测试临界值:1%水平-2.5789675%水平-1.94275710%水平-1.615431
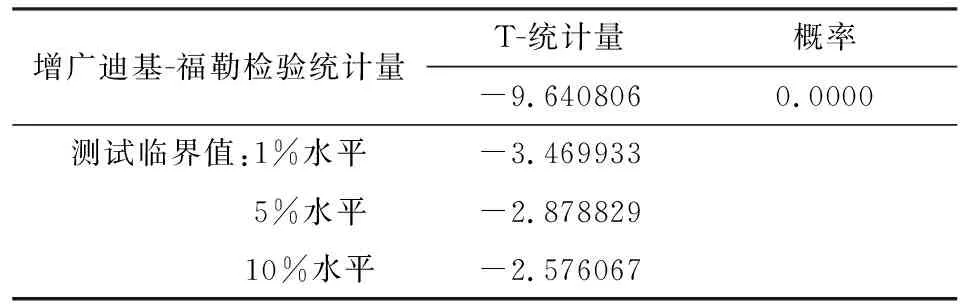
表2 原序列单位根检验结果
2.3 ARIMA模型识别
通过自相关和偏自相关分析,并经试验后可能的模型组合有ARIMA(2,2,1),ARIMA(2,2,2),ARIMA(2,2,3),ARIMA(1,2,3)。对初步判断出的模型进行试验,结合各模型的AIC值大小来选择最终模型,四个模型的相关指标见表3。
比较各模型的指标值,ARIMA(2,2,3)的R2最大,且根据AIC准则,选择AIC最小的,综合分析认为选择ARIMA(2,2,3)模型合适。
3 实证分析
3.1 政策实施点确定
在应用“投射-施后”对比分析评估法的过程中,确定政策实施点是前提。本文梳理了2000~2016年国家宏观管理部门出台的煤炭产业调控政策,见表4。选取2004年12月15日启动煤电价格联动机制[11]、2008年6月19日全国发电用煤临时价格干预限价[12]、2016年3月21日启动276工作日三个政策实施点,分别设置为政策Ⅰ、政策Ⅱ、政策Ⅲ,分阶段对政策实施之后做短期预测,与实际煤炭价格对比,估计政策实施效果。

表3 模型相关指标

表4 煤炭相关政策
3.2 模型的预测与政策效应
ARIMA模型预测结果见表5,政策Ⅰ样本长度最大,相应地误差最小。政策Ⅰ样本区间内,煤炭价格波动幅度小,预测模型拟合度高。政策Ⅱ误差最大,样本区间内煤炭价格波动剧烈,模型拟合难度较大,所以误差大[13]。
根据政策“投射-实施后”对比分析法,政策效果公式E=A2-A1,其中A1在本实验中指代的是动态Y(12M)的值,即动态预测12月份的煤炭价格;A2指代的是实际值(12M),即12月份实际煤炭价格观测值。这是考虑到12月份之后进入下一年工作调整等变化因素较多,因此选12月份为政策实施效果点进行政策效果的度量,最终政策效果见表6。
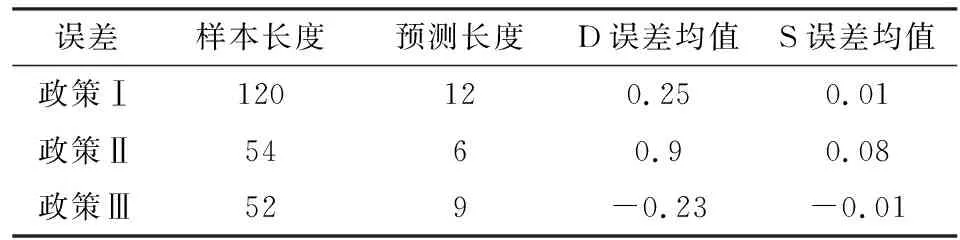
表5 ARIMA预测结果

表6 政策效果
在进行预测时,所用预测模型自回归是滞后两期的,随机干扰滑动平均是滞后三期的,也就是预测点开始之后的第四期预测值是政策实施后的值作为因变量形成的。假设模型正确的前提下,说明了政策的实施效果的完全体现至少滞后三期,因为前三期的效果都还包括政策实施前的影响因子,会对政策的实施形成干扰。这与政策下发后需要传达、政策领会、制定方案,需要预留一定的政策准备期是一致的。
为提高政策效应评估精度,本文提出利用ARIMA模型的两种预测方式(即静态预测和动态预测)修正政策效应估计值。静态预测值Y静与动态预测值Y动是在相同的机制下形成的,区别就是滞后期的值不同,我们可以认为静态Y是含有政策因素的,且与动态Y形成机制相同,而动态Y不包括政策因素,因为动态Y公式右边的值全部是政策实施前的值,所以用静态Y值减去动态Y值来作为政策实施的效果更准确。因此修正政策效果公式为E修=Y静-Y动,修正后的政策效果见表7。

表7 修正后的政策效果
从修正后的政策效果可以看出,政策Ⅱ和政策Ⅲ的效果绝对值增大,政策Ⅰ绝对值变小。我们可以理解为政策Ⅱ和政策Ⅲ实际值受到了更多因素的干扰,因此实际值相对偏小。而静态预测值的获得模式与动态预测值的获得模式相同,静态预测值中也包括干扰因素,但是相对来说干扰因素起的作用小,对实验造成的干扰少。
根据对政策效果的估计,三次煤炭产业调控政策都在一定程度上起到了预期效果,影响了我国的煤炭价格,但在不同的经济状态下,政策效果的大小差别很大,政策Ⅲ的实施效果最为显著[14]。政策Ⅲ的目的是在规范和改善煤炭生产经营秩序,有效化解过剩产能的基础上推动煤炭企业实现脱困发展。政策Ⅲ的实施,从根本上扭转了连续5年下降的煤炭价格[15],进而达到推动煤炭企业脱困发展的预期目标。
4 结 语
通过分析三次政策实施对比效果,可以看出用静态Y(ARIMA模型静态预测值)和动态Y(ARIMA模型动态预测值)相减得到的差值作为政策效果的估计更为可靠,本文构建的评估方法既可以应用于以影响煤炭价格作为预期目标的政策有效性评估,也可以拓展应用于以煤炭产量、消费量等其他变量作为调控预期的相关产业政策有效性的评估。
