Decay Analysis of Ge Isotopes Formed in Reactions Induced by Tightly and Loosely Bound Projectiles∗

Amandeep Kaur,Kirandeep Sandhu,and Manoj K.Sharma

1School of Physics and Materials Science,Thapar Institute of Engineering and Technology,Patiala 147004,Punjab,India

2Department of Physics,GSSDGS Khalsa College,Patiala 147001,Punjab,India

AbstractThe dynamical cluster-decay model(DCM)is employed to investigate the decay of68,70Ge∗compound nuclei formed respectively via tightly(4He)and loosely(6He)bound projectiles,using64Zn target.The study is carried out over a wide energy range(Ec.m.∼5 MeV to 16 MeV)by including the quadrupole deformations(β2i)and optimum orientationsof the decaying fragments.The fusion cross-sections,obtained by adding various evaporation channels show nice agreement with the experimental data for4He+64Zn reaction.The contribution from competing compound inelastic scattering channel is also analyzed particularly for68Ge∗nucleus at above barrier energies.On the other hand,the decrement in the fusion cross-sections of70Ge∗nuclear system is addressed by presuming that65Zn ER is formed via two different modes:(i)the αn evaporation of70Ge∗ nucleus,and(ii)1n-evaporation of66Zn∗ nuclear system,formed via breakup and 2n-transfer channels due to halo structure of the6He projectile.Besides this,the suppression in 2np evaporation cross-sections suggests the contribution of another breakup and transfer process of6He i.e.4He+64Zn.The contribution of breakup+transfer channels for6He+64Zn reaction is duly addressed by applying relevant energy corrections due to the breakup of“6He” projectile into 2n and4He.In addition to this,the barrier lowering,angular momentum and energy dependence effects are also explored in view of the dynamics of chosen reactions.

Key words:tightly and loosely bound projectiles,evaporation residue,breakup and transfer

1 Introduction

Over the last few decades,the reactions induced by tightly and loosely bound projectiles have catched the extensive attention of the nuclear physics community.It is so because the nature of projectile plays very important role in the formation and decay process of the compound nucleus(CN).Generally,the CN formed via tightly bound projectile disintegrates through light particle emission or heavy mass fragments such as fusion- fission( ff)channels.The probability of each decay channel depends upon the mass of CN,excitation energy(E∗CN)and related angular momentum(ℓ)etc.However,when a loosely bound projectile strikes the target,the breakup and transfer processes also start contributing towards the fusion component.The loosely bound halo projectile gets disengaged in the field of target into two parts,from which one part of the projectile is transferred to the target to form an excited compound system,while the other escapes with relatively unchanged velocity.This breakup+transfer process leads to loss of flux from the fusion channel and thus suppress the cross-section,especially at energies in the vicinity of the Coulomb barrier.[1−2]In fact,the larger radius of loosely bound projectile decreases the Coulomb barrier,which leads to enhancement in the fusion cross-sections at near and sub barrier energies.On the contrary,at above barrier energies the breakup of loosely bound halo nucleons due to low binding energy,give rise to the reduction in complete fusion(CF)cross-sections,known as fusion suppression.[3−5]In the recent years,the reactions induced by unstable nuclei around the neutron drip line with mass A<20 are vigorously used to investigate various reaction mechanisms such as fusion,breakup and transfer etc.[6−9]Beside this,the total reaction cross-sections(σreac)are also studied extensively within the application of tightly bound projectiles,bombarding with wide range of target nuclei such as9Be to208Pb.[10−11]The decay of CN formed in such reactions,leads to various reaction channels of light particles(LPs)emission and heavier fragments such as fusion- fission.The possibility of the compound inelastic scattering may also be perceived for these reactions.[12]Interestingly,it is observed that the total sum of all open channel cross-sections(σreac)is identical to the cross-section calculated from analysis of elastic scattering angular distributions.[13]Therefore,it would be of interest to understand the structure effects and dynamics involved in reactions induced by both tightly and loosely bound nuclei.

In view of the above discussion,the present work is carried out to analyze different decay mechanisms governed via tightly(4He)and loosely(6He)bound projectiles using same target nucleus(64Zn)within the framework of dynamical cluster-decay model(DCM).[14−19]In the recent experiments,[13,20−21]the reaction cross-sections have been measured for the decay of68Ge∗and70Ge∗compound nuclei formed respectively in4He+64Zn and6He+64Zn reactions,over the wide range of center-of-mass energies Ec.m.∼(5–16)MeV.The total cross-sections for these reactions are considered to have the contribution from the complete fusion and other processes such as compound inelastic scattering,breakup,transfer etc.Note that,in both reactions the fusion process leads to the production of evaporation residues(ERs),hence σfus≈ σER,as the contribution of the ff-channel is not significant for4He+64Zn and6He+64Zn reactions.

The68Ge∗nucleus formed via4He beam,mainly deexcites by one-and two-particle evaporation channels like γ,n,p,2p,nα,pα,and 2α. Interestingly,oneparticle emission is the dominant for68Ge∗nuclear system,whereas the contribution of nα,pα,and 2α is negligible.[13,20]The experimental excitation functions of these evaporation channels are addressed individually by optimizing the only parameter of the model,known as neck-length parameter∆R.Moreover,another competing channel i.e.compound inelastic scattering for4He+65Zn reaction is also investigated,in particular at the above barrier energies.In addition to this,the fusion cross-sections are addressed for70Ge∗nucleus by summing all the excitation functions of(2n)68Ge,(np)68Ga,(2np)67Ga and(nα)65Zn evaporation residues.The comparison between the calculated and experimental fusion cross-sections for6He+64Zn→70Ge∗reaction suggests the contribution of breakup and transfer events arise due to the halo structure of the6He projectile.It may be noted that,65Zn ER is also formed via breakup and two neutron transfer process,in addition to the αn evaporation channel.[21]In addition to this,the suppression in 2np cross-sections is associated with the incomplete fusion of other part of6He projectile with the target i.e.6He+64Zn.Thus,an effort is made to estimate the breakup+transfer contribution by including the relevant energy corrections in reference to the breakup of6He projectile into4He and 2n,which is responsible for the enhancement of the total cross-sections in comparison to the ones calculated for4He+64Zn→68Ge∗reaction.

The outline of the paper is as follows:Section 2 gives a brief description of the dynamical cluster-decay model(DCM).The DCM based calculations for the4He+64Zn and6He+64Zn reactions at various centre-of-mass energies(Ec.m.)are given in Sec.3. The calculations are made for the choice of deformed fragments having(β2i)quadrupole deformations with“optimum”orientations taken from.[22]Finally,the results are summarized in Sec.4.

2 Theoretical Framework

Based on quantum mechanical fragmentation theory(QMFT),[23−25]the dynamical cluster-decay model(DCM)is used here to study the decay mechanism of hot and rotating nuclear systems.This model is worked out in terms of collective coordinates of mass and charge asymmetriesand ηZ=(Z1−,the relative separation R,the multipole deformations βλi(λ=2,3,4)and orientations θi,where i=1 and 2 stand for heavy and light fragments.For the decay of a excited nucleus,the η and R coordinates refer,respectively,to nucleon division or exchange between outgoing fragments and the transfer of kinetic energy of the incident channel(Ec.m.)to the internal excitation of the outgoing channel.

The stationary Schrödinger equation in η coordinate,at a fixed R=Ra(the first turning point of barrier penetration shown in Fig.1),is written as

with ν =0,1,2,3,...referring to ground state(ν=0)and the excited statesolutions.The mass parameter Bηηare the smooth hydrodynamical masses of Kröger and Scheid.[26]By solving Eq.(1),we get the preformation probability P0,which imparts the important structure information of the decaying nucleus and reads as

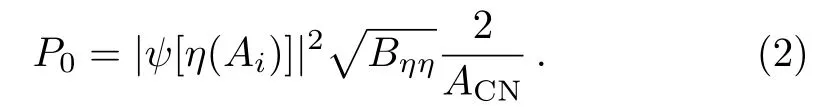
The fragmentation potential VR(η,T)used in stationary Schrödinger Eq.(1)in η,at fixed R is defined as

Here the VR(η,T)calculated in macro-microscopic method of Strutinsky,where VLDMis the temperature dependent liquid drop energy of Davidson et al.[27]with its constants refitted at T=0,[28]give the experimental binding energies of Audi et al.[29]or theoretical estimates of Möller et al.[30]wherever not available in Ref.[29].The “empirical”shell correction(δU)of Myers and Swiatecki,[31]also made T-dependent to vanish exponentially at T0=1.5 MeV.[32]The other terms VC,VP,and Vℓare,respectively,the Coulomb,nuclear proximity,and centrifugal potentials for deformed and oriented nuclei.The Coulomb potential for multipole-multipole interaction between two separated nuclei is given by

and the nuclear proximity potential for deformed,oriented nuclei employing temperature effects,reads as

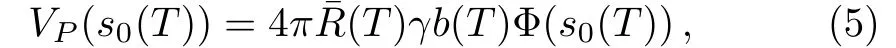
where b(T)is the nuclear surface thickness,γ is the surface energy constant,¯R(T)is the mean curvature radius and Φ(s0(T))is the universal function(for more details see Refs.[33–34]).The angular momentum effects are included via the following expression

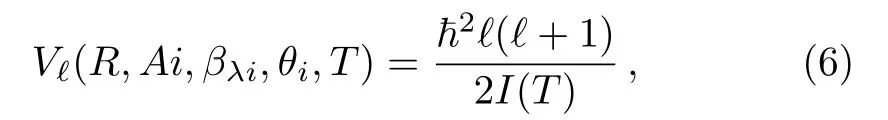
with moment of inertia I(T)in completes ticking limit,i.e.,or,alternatively,the one calculated in non-sticking limit INS=µR2.Note that the alternative use of non-sticking limit corresponds to the supposition of prompt emission of fragments,generally used in the experimental determination of the ℓ-value.We find that the sticking limit(IS)used in the present work is more appropriate for the proximity potential,which inturn result in higher ℓ-values.Hence,the angular momentum values are larger for sticking moment of inertia and correspond to smaller separation distance∆R,while the process is vice versa for INS.

In terms of collective coordinates,the compound nucleus decay cross sections,for ℓ-partial waves is given by

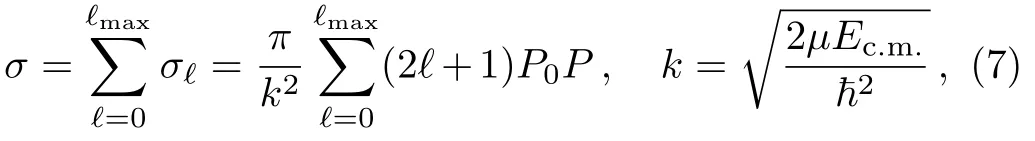
where the preformation probability P0(given in Eq.(2))refers to η-motion and the penetrability P defined later to R-motion.ℓmaxis the maximum angular momentum,fixed here for the light particle cross-section approaching zero.The tunneling probability P is given by the Wentzel-Kramers-Brillouin(WKB)integral

with V(Ra,T)=V(Rb,T)=TKE(T)=Qeff(T)for the two turning points.V(Ra,T)acts like an effective Q value of decay,Qeff(T),and TKE(T)as the total kinetic energy of decaying fragments.The turning point Raof barrier penetration is given as

with radius vectors(i=1,2)

and T-dependent nuclear radii R0iof the equivalent spherical nuclei read as,[35]

The temperature T is related to the incoming center-of mass energy Ec.m.or the compound nucleus(CN)excitation energy E∗CNvia the entrance channel Qinvalue asIn Eq.(9),the“∆R”is the separation distance between the surfaces of decaying fragments,known to assimilate the neck formation effects,and hence referred as the neck-length parameter.This choice of neck criteria is very much similar to the one used in scission point[36−37]and saddle point[38−40]statistical models for addressing evaporation residue and fission decay modes.It is worth noting that the neck-length increases as a function of center-of-mass energy(Ec.m.)(see Fig.5(a)).The neck values lie below 2.5 fm due to the use of proximity potential.The necklength ∆R or,equivalently,the first turning point Rais the only parameter of the model,and inturn to define the effective “barrier-lowering” parameter ∆VB(ℓ)as the difference between the actually used barrier V(Ra,ℓ),and the calculate barrier VB(ℓ),as

∆VB(ℓ)represents a negative quantity,owing to the fact that penetration can occur below the barrier only.

3 Results and Discussions

In the present work,we intend to study various decay paths of68,70Ge∗nuclear systems using the dynamical cluster decay model(DCM)[14−19]at center-of-mass energies(Ec.m.∼5 MeV to 16 MeV)lying in the vicinity of the Coulomb barrier.First,in Subsec.3.1,the calculations are made for the evaporation residues of the68Ge∗compound nucleus formed via interaction of tightly bound4He beam on64Zn target.In the subsequent analysis,the dynamics of6He+64Zn→70Ge∗reaction is explored in Subsec.3.2,by investigating the fusion,breakup and transfer channels,where breakup+transfer events arise due to the halo structure of6He projectile.Finally,a comparative study of tightly and loosely bound projectile induced nuclear reactions is carried out to analyze the influence of halo structure of the projectile on the considered reaction dynamics.

3.1 Decay of68Ge∗Nucleus Formed Using Tightly Bound4He Beam

The interaction of alpha particle with64Zn target leads to the formation of68Ge∗compound system,which deexcites via various evaporation channels such as γ,p,n,2p,nα,pα,and 2α.[20]It is suggested in Refs.[13,20]that within Ec.m.∼ (5–16)MeV energy range,the one-particle(p and n)evaporation channels are dominant,whereas negligible contribution of the two-or multi-particle decay modes is observed.Moreover,the γ-channel is also not included in the present calculations due to negligible cross-sections,contributing towards the total reaction cross-sections.[13]Apart from these decay events,the contribution from another competing channel,i.e.,compound inelastic scattering is also investigated particularly at higher centre-of-mass energies.Hence in the present section,an attempt is made to address the dynamics of4He+64Zn reaction by understanding various decay modes of68Ge∗nucleus.

In order to understand the dynamics involved through the one particle emission,the barrier characteristics of68Ge∗→ p+67Ga and68Ge∗→ n+67Ge decay channels are plotted in Fig.1(a)at highest incident energy Ec.m.=15.17 MeV and extreme angular momentum states ℓ=10~and 41~.Interestingly,both the decay channels show different barrier characteristics at differentℓ-states.Clearly,at ℓmin=10~,the barrier height(VB)is higher for proton-emission in comparison to the neutrondecay,and is maintained upto ℓ=22~as depicted from Fig.1(b).However,these results show reverse trend at higher angular momentum states up to ℓmax=41~.This may be due to the interplay between the various potentials contributing towards the barrier height.In order to explore this,Fig.2(a)is plotted,which shows the variation of the centrifugal potential for proton and neutron emissions at different angular momentum states. The centrifugal potential remains higher for neutron-decay for majority of ℓ-states.The same is true for the proximity potential,but not shown here.However,with the addition of the Coulomb term in Fig.2(b),the magnitude of the potential for the neutron emission decreases for lower ℓ-values,leading to higher barrier height for the proton decay.Elaborating this,the larger barrier height for the proton emission at lowest ℓ-state is mainly due to the dominance of Coulomb term at lower angular momentum states,where the suppression in the magnitude of the centrifugal potential is simultaneously observed.At lower ℓ-states, ℓ(ℓ+1) ∼ ℓ2term in the centrifugal potential,given by Eq.(6)does not contribute much,hence the dominance of Coulomb factor can be felt for the proton decay.However,the Coulomb potential remains zero for the neutron emission resulting higher barrier for the proton at ℓmin=10~state.In contrast to this,the magnitude of the centrifugal potential competes the Coulomb term and gradually becomes larger in magnitude for the higher ℓ-values.Due to less influence of the Coulomb term at higher ℓ-states,the barrier height gets suppressed for the proton emission(see Fig.1(b)).In other words the Coulomb and centrifugal potentials play an important role to define the barrier characteristics of the proton and neutron decays.Note that the emergence of the flip due to different barrier characteristics for proton and neutron emission channels also effect the penetration path(see Fig.2(c)).In addition to the barrier height,barrier width also plays an important role to describe the penetration of the fragment through the barrier,as described by Eq.(8)of Sec.2.Depending on these factors,the penetrability P shows different behavior for p-and n-decay channels,plotted in Fig.2(c).Specifically,the variation of decay barrier widthcan be depicted from the inset of Fig.2(c)to illustrate the fact that penetrability increases exponentially with decrease in barrier width and vice versa.However,we notice that P increases with increase in ℓ for both decay channels and in turn sets the minimum value of angular momentum,slightly different for both particles.

Fig.1 (a)Scattering potential V(R)for68Ge∗ → p+67Ga and68Ge∗ → n+67Ge decay channels at Ec.m.=15.17 MeV,calculated for two extreme ℓ-values, and ℓmax=41~.(b)Variation of DCM-calculated decay barrier height(VB)as a function of angular momentum ℓ(~)for both emissions.

In the next step,to investigate the fragmentation path of68Ge∗nucleus via p-and n-particle evaporation channels,the mass-fragmentation potential V(A2)is shown in Figs.3(a)and 3(b)at Ec.m.=15.17 MeV.Note that the fragmentation potential goes as an input to the Schrödinger equation,which is used to estimate the preformation probability P0,and hence the excitation functions of the nuclei.The results are obtained for both the decay channels using different separation distances(∆R)chosen to fit the respective experimental data.In order to see the comparative contribution of energetically feasible fragments,the fragmentation paths are plotted forℓminand ℓmaxvalues.One may notice from Figs.3(a)and 3(b)that the structure of potential energy surfaces(PES)are almost independent at two extreme ℓ-values for the fission fragments(FF),but the characteristic behavior of fragmentation potential for light particles(LPs)is significantly different.At lower ℓ-values,the emission of light particles is favorable that means contribution of pand n-particles is prominent,whereas fission fragments(marked in figure as FF)start competing the light particles at higher ℓ-states.Following this,an attempt is made to predict the fission cross-sections for the decay of68Ge∗nucleus within the framework of DCM,which may be verified by future experiment(s)(refer Table 2).

Fig.2 (a)Variation of the centrifugal potential Vℓfor the proton and neutron emissions with angular momentum ℓ(~)at highest center-of-mass energy Ec.m.=15.17 MeV.(b)Same as that of(a),but plotted for Coulomb+centrifugal potentials.(c)Variation of DCM-calculated barrier penetrability(P)as a function of angular momentum ℓ(~)for both emissions.The inset of(c)shows the behavior of barrier width varying with angular momentum.

After analyzing the ℓ-dependence of fragmentation decay path for both decay channels,the effect of center-of mass energy on the fragmentation potential(V),preformation probability(P0)and barrier penetrability(P)is illustrated in Figs.4(a),4(b),and 4(c)respectively,at two common ℓ=15~and 41~angular momentum states.These calculations are done at common neck-length parameter∆R,chosen to fit the p-evaporation channel crosssections.Clearly,the magnitude of fragmentation potential increases slightly with center-of-mass energies Ec.m.for p-and n-particle emissions.Interestingly,the fragmentation potentials for both particles overlaps at the ℓ=15~angular momentum state,indicating the fact that neutron and proton emissions are equally probable at lower angular momentum states.On the other hand,for higher angular momentum the fragmentation behavior of the pand n-decay channels differs significantly.For example at ℓ=41~,the fragmentation potential is much higher for the neutron-emission as compared to proton-decay.Lower fragmentation potential for the proton-decay seems to suggest that the proton emission is more favorable towards decay at highest angular momentum state.This result is in accordance with the observation of Fig.1(a),where lower barrier is reported for the proton emission at ℓmax=41~.This difference in fragmentation potential of n-and p-decay channels at higher ℓ-values enters primarily via rotational energy term due to difference in moment of inertia,as different daughter nuclei are produced in these two channels.It may be noted that67Ga(the daughter nucleus in p-channel)is prolate deformed with β2=0.228,whereas67Ge(the daughter nucleus in n-channel)is oblately deformed with β2= −0.299.As their radii are changed significantly,so moment of inertia changes accordingly.It is important to mention here that the minima in the fragmentation potential corresponds to maxima in preformation probability and vice versa.Thus,the preformation factor P0shows opposite trend than that of the fragmentation potential in reference to the ℓ-value.One can see from Fig.4(b),at lower ℓ-value,both n-and p-particles have almost same and maximum preformation probability,which in turn,represents that LPs are favorable at lower ℓ-states for all energies.Whereas,at higherℓ,the P0has much lower magnitude,this is in agreement with Fig.3(a)for the fragmentation case.Next,the variation of penetrability P is defined via Fig.4(c),it shows similar results as shown by fragmentation potential,owing maximum magnitude at higher ℓ-state,and indicating the different barrier characteristics for both the particle emissions.Also,barrier penetrability(P)shows increment with increase in center-of-mass energy particularly at lower angular momentum.

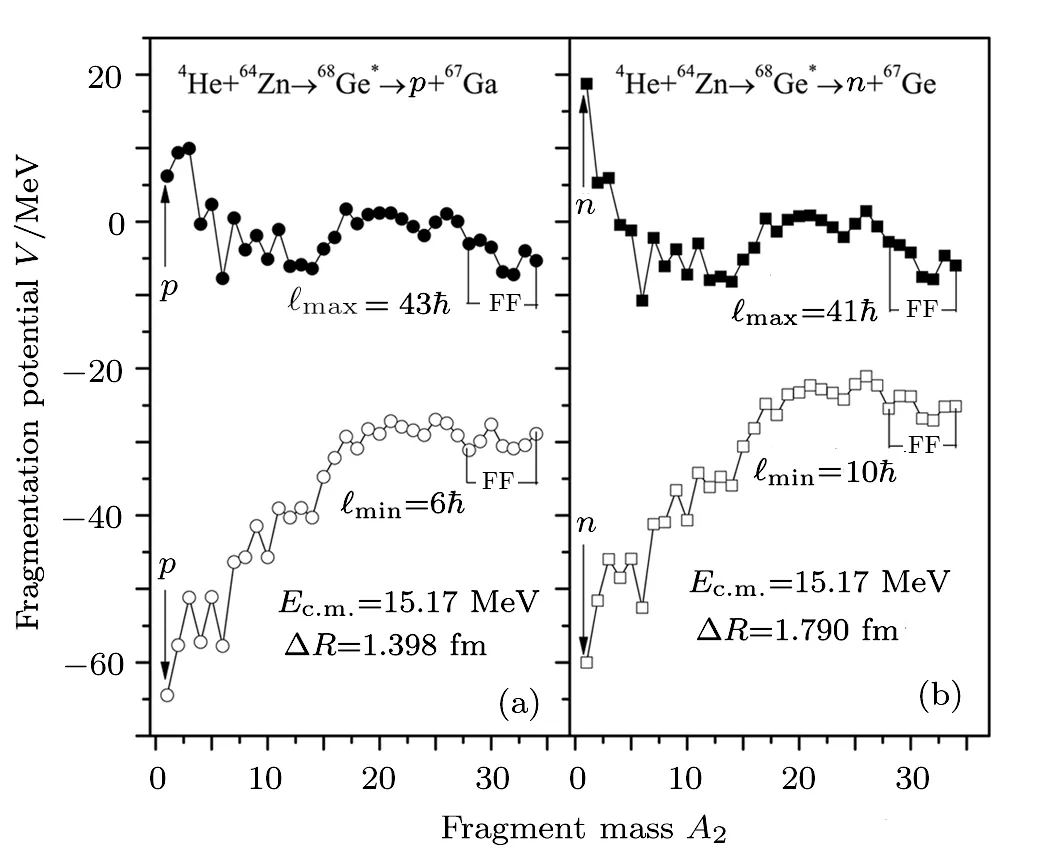
Fig.3 Mass-fragmentation potential V(A2)at centre-of-mass energy Ec.m.=15.17 MeV for(a)64Zn(4He,p)67Ga and(b)64Zn(4He,n)67Ge decay channels,using best- fit ∆R’s,plotted for ℓminand ℓmaxvalues.

Fig.4 The energy(Ec.m.)dependence of(a)fragmentation potential(V),(b)preformation probability(P0)and(c)penetrability(P)for proton and neutron evaporation channels at two ℓ-values,15~and 41~.

Using the combined effect of P0and P values,the ER cross-sections for p-and n-decay channels are calculated within the framework of DCM,presented in Tables 1–2,and compared with experimental data.[13,20]The DCM calculated results show nice agreement with the experimental measurements.The only parameter of the model is the neck-length(∆R),which decides the first turning point of the penetration path,obtained for best- fit of the measured data,listed in the tables and plotted in Fig.5(a).The optimized neck-length parameter“∆R”is observed to have larger magnitude for n-channel as compared to that of p-channel.It may be due to the reason that68Ge appears below the β stability line and hence seems more prone for p-emission,which is in agreement with the result depicted in Fig.4(a).As discussed earlier,the fission fragments(FF)may also contribute in the decay of68Ge∗nucleus,particularly at higher ℓ-states.Thus,in this work an effort is made to predict the fission contribution pre-sented in Table 2,using∆RFF= ∆Rn−0.5 fm.It is relevant to mention that lighter fragments are generally emitted first from the hot and rotating nuclei,establishing the fact that light particle emission occurs prior to the fission process.Keeping this in mind,higher∆R is considered for ER formation as compared to the fission decay.Similar analysis is carried out in the previous work[41]of DCM,based on the decay of Xe-nucleus.At different neck-length parameters“∆RFF”,the predicted excitation functions of fission fragments(A2=28–34 and their complementary fragments)are found to be negligibly small,indicating the fact that Ge-nucleus decays primarily via light particles,and fission fragments contribution is negligibly small.Moreover,if we calculate FF cross-sections at∆RFF=∆Rp−0.5 fm i.e.at the neck-length parameter of proton emission,the fission contribution reduces further.Hence the collective clusterization does not reinforce the fragmentation to follow the fission path,instead ER formation is preferred.In addition to this,the“barrier modification” (∆VB)another observable of DCM,which can be related to the∆R(equivalently,Ra),is examined in Fig.5(b)as a function of Ec.m..Apparently,∆VB(in magnitude)for each particle emission is maximum for lowest Ec.m.and minimum at the highest one.It is also evident from figure that larger barrier modification is needed for the case of proton-emission in comparison with neutron one.

Table 1 The calculated decay cross-sections for p-evaporation channels using DCM at various Ec.m.for4He+64Zn reaction and compared with experimental data.[13,20]The other related observables like neck-length parameter(∆R)and temperature(T)are also listed.

One-particle emission is dominant decay mode of68Ge∗nucleus,as explained in Sec.1 of the present work.However,experiments[13,20]also suggest that two-particle emission channels play significant role at energies above 20 MeV due to the large threshold of multi-nucleon clusters.Although,in this work we are dealing with energies below 20 MeV,but an effort is made here to check the relative contribution of two-particle emission for the decay of68Ge∗nucleus formed in4He+64Zn reaction.The cross-sections of68Ge∗→2p+66Zn and68Ge∗→ αn+63Zn decays are calculated at two extreme energies Ec.m.=5.79 MeV and 15.17 MeV.The DCM calculated crosssections are comes out to be σ2p=1.77 × 10−4mb and σαn=1.35 × 10−2mb at lowest Ec.m.=5.79 MeV,which increases with increase in centre-of-mass energy and read as σ2p=1.27 mb and σαn=15.17 mb at highest Ec.m.=15.17 MeV.These cross-sections are calculated at same∆R as observed for p-emission,because the previous study[18]of DCM indicates almost similar magnitude of∆R for one-particle and multi-nucleon emissions.Hence it is evident from above discussion that the estimated crosssections for 2p and αn do not contribute much towards the total reaction cross-sections,as reported in the experimental work.[20]

Table 2 Same as Table 1 but for n-evaporation channel.In addition to this,the predicted fission contributions(σFF)are also listed.

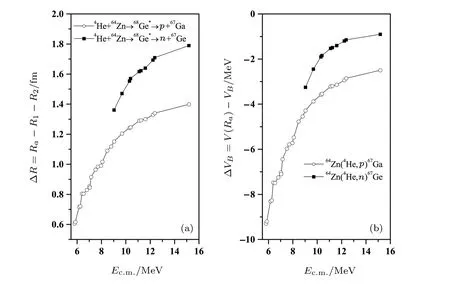
Fig.5 Variation of(a)the neck-length parameter(∆R)and(b)the barrier modification(∆VB)as a function of Ec.m.for the decay of68Ge∗compound system via neutron(solid squares)and proton(open circles)decay channels.

Apart from one-and two-particle evaporation channels,the compound inelastic scattering is another competing channel emerging in the decay of68Ge∗compound system especially at above barrier energies.In this process,the projectile is absorbed by the target nucleus and leads to formation of compound nucleus(CN),which further re-emits the incident particle with low kinetic energy,thus original nucleus remains in the excited state.Here,we have studied the compound inelastic scattering for4He+64Zn →68Ge∗→4He′+64Zn reaction.For inelastic scattering process,the entrance channel keeps its identity,and hence the preformation probability is taken P0=1 for(4He,4He′)decay channel,and penetrability is calculated using WKB approximation and presented in Fig.6.It is evident from Fig.6 that larger penetration probability is obtained at highest center-of-mass energy,indicating easier penetration of the projectile like fragments.Besides this,the penetrability corresponding to each ℓ-state increases with increase in angular momentum.Using P0and P,the measured[13]cross-sections of(81±13.8)mb and(201±37.1)mb are best fitted at∆R=0.699 fm and 0.827 fm values respectively,for two highest energies Ec.m.=11.29 MeV and 15.17 MeV,at which signature of the inelastic scattering is observed.It is relevant to mention that,if energy loss up to 30%is considered in the inelastic scattering process then the neck-length parameter“∆R”and angular momentum effect remain almost unchanged.Hence,negligible change in ∆R and ℓmaxvalues is observed even with the reduction of 30%in the energy of incident flux.

Fig.6 Barrier penetrability P as a function of ℓ for 64Zn(4He,4He′)64Zn reaction plotted at two center-of mass energies.

3.2 Decay of70Ge∗Formed via Loosely Bound Projectile6He

After analyzing the dynamics of tightly bound4Heinduced reaction,we intend to explore the decay of excited70Ge∗nuclear system formed via interaction of two neutron halo “6He” projectile and64Zn target.Interestingly,in recent experiment,[21]6He+64Zn→70Ge∗reaction has been studied at various energies across the barrier ranging Ec.m.=(7.54 to 16.1)MeV.The total fusion cross-sections(σfus)have been obtained by measuring the excitation-functions of various evaporation residues(ERs)(2n)68Ge,(np)68Ga,(2np)67Ga,and(nα)65Zn,as light charged particle emission is the primary decay mode of70Ge∗nuclear system. Apart from ERs,the breakup and transfer events also contribute to the total crosssections due to loosely bound nature of the6He projectile.Hence in the present section,the evaporation residue,breakup+transfer cross-sections(or equivalently incomplete fusion cross-sections)are addressed using DCM,in order to have overall understanding of the dynamics of6He+64Zn→70Ge∗reaction so that loosely bound nature of6He nucleus be explored.The detailed analysis of the above work is carried out in the subsequent discussion.

In order to investigate the decay of70Ge∗nucleus,the fragmentation potential V(ℓ)and preformation probability P0(ℓ)are presented in Fig.7 for the evaporation residues of70Ge∗nucleus,corresponding to energy Ec.m.=12.7 MeV,above the Coulomb barrier.The different ER decay modes,which are shown in figure represent multi-nucleon clusters and heavy residual nuclei,i.e.,X+Y→2n+68Ge(solid squares),np+68Ga(open squares),2np+67Ga(solid triangles)and nα+65Zn(open triangles).Clearly,the fragmentation potentials for all ER channels show increment with increase in angular momentum.The result reflects that light charged particle emission is probable at small values of angular momentum states,due to lower fragmentation potential and larger preformation probability,as depicted from Figs.7(a)and 7(b)respectively.It is relevant to mention that similar results are extracted for the decay of68Ge∗compound nucleus,where the evaporation residue formation dominates at lower angular momentum states.In addition to this,Fig.7(a)shows that at lower ℓ-values,the fragmentation potential increases with increase in mass of the multi-particle cluster,i.e.,maximum for nα and minimum for 2n cluster,whereas reverse trend is observed at higher angular momentum values.As explained earlier in Subsec.3.1,this happens because of the relative contribution of Coulomb,proximity and centrifugal potentials to the total fragmentation potential.Due to this,an flip in the magnitude of the fragmentation potential arises around ℓ=30~.Similar results are obtained from Fig.7(b),plotted for the preformation probabilities of the decay fragments.The preformation probability shows increment up to certain ℓ-states,then sharply decreases near the ℓmax-values of the cluster emission.The maximum values of the angular momentum can be estimated from Fig.7(b),designated as a point where the contribution of the preformation probability is negligible.Above theℓmax-values the total cross-sections becomes significantly small.

In reference to above discussion,the angular momentum window ℓmin≤ ℓ≤ ℓmaxis fixed and the excitation functions for the evaporation residues of70Ge∗nucleus are estimated using Eq.(7).The ℓminfor all the decay fragments lies around 0~,and ℓmax-values are pointed in Fig.7(b),which are different for different clusters.The fitted cross-sections are tabulated in Table 3 for all the mentioned clusters.The best- fit values of neck-length parameters(∆R)for individual ER channels along with temperature(T)and center-of-mass energies(Ec.m.)are also listed in Table 3.Different∆R values indicate unique reaction time scales for individual evaporation residue channels.It is of interest to note that the total calculated fusion crosssectionsof70Ge∗compound system,i.e.,sum of individual ER excitation functions,deviate from the experimental measured fusion cross-sectionsIt is clearly depicted from Fig.8(a)and 8(b)that the 2n and np clusters show nice agreement with the experimental data.However,the strong mismatch of the experimental and our DCM based cross-sections is obtained for the(nα)65Zn-cluster(see Fig.8(c)),which is responsible for the decrement in the fusion cross-sections and signify the large contribution of breakup and transfer channels.Additionally,the cross-sections of 2np-cluster are also underestimated at above barrier energies as shown in Fig.8(d).The results remain intact even at the maximum allowed neck-length parameters.Hence the wide range of∆R could not address the experimental crosssections upto∼ 2.5 fm.The suppression in the nα and 2np cross-sections is governed mainly through the loosely bound nature of the6He projectile,responsible for the breakup and transfer events.The loosely bound6He nucleus breaks up into two parts4He and 2n,which act as new projectiles and interact with the64Zn target nucleus individually.It may be noted that65Zn nucleus is not formed only via nα evaporation channel,but also find its genesis in the breakup and two-neutron transfer channels of6He projectile,which is addressed in the subsequent discussion,by employing the relevant energy correction.Also,the suppression in 2np cross-sections is associated with the incomplete fusion of other part of6He projectile with the target i.e.4He+64Zn.In reference to the above discussion,the contribution of breakup and transfer channels is included in the present analysis as the difference between estimated and experimental cross-sections,which are read as

Note that the efficacy of DCM in reference to breakup of loosely bound projectile and interaction of its one part with the target has been analysed in previous studies.[18−19]The 2n and4He now act as new projectiles and interact with the64Zn target nucleus individually,and lead to the formation of66Zn∗and68Ge∗nuclear systems,which further decays via n+65Zn and 2p+66Zn channels respectively.In the above process,the energy correction is required to address the breakup+transfer process,because the interaction energy must be modified according to the charge and mass number of the new projectiles.The corrected energy(Ec)of new projectile is obtained as[19]

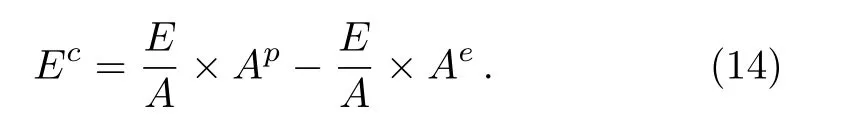
Here Apis the mass of projectile before breakup and Aeis mass of ejectile,which is an uninteracted outgoing fragment. Hence by including the relevant energy corrections,we look for the breakup and transfer processes and subsequently the decay of66Zn∗and68Ge∗nuclear systems.The modified center-of-mass energiesand respective excitation energiesare listed in Table 4.The corrected energies for breakup channels are smaller in magnitude as compared to the fusion process.

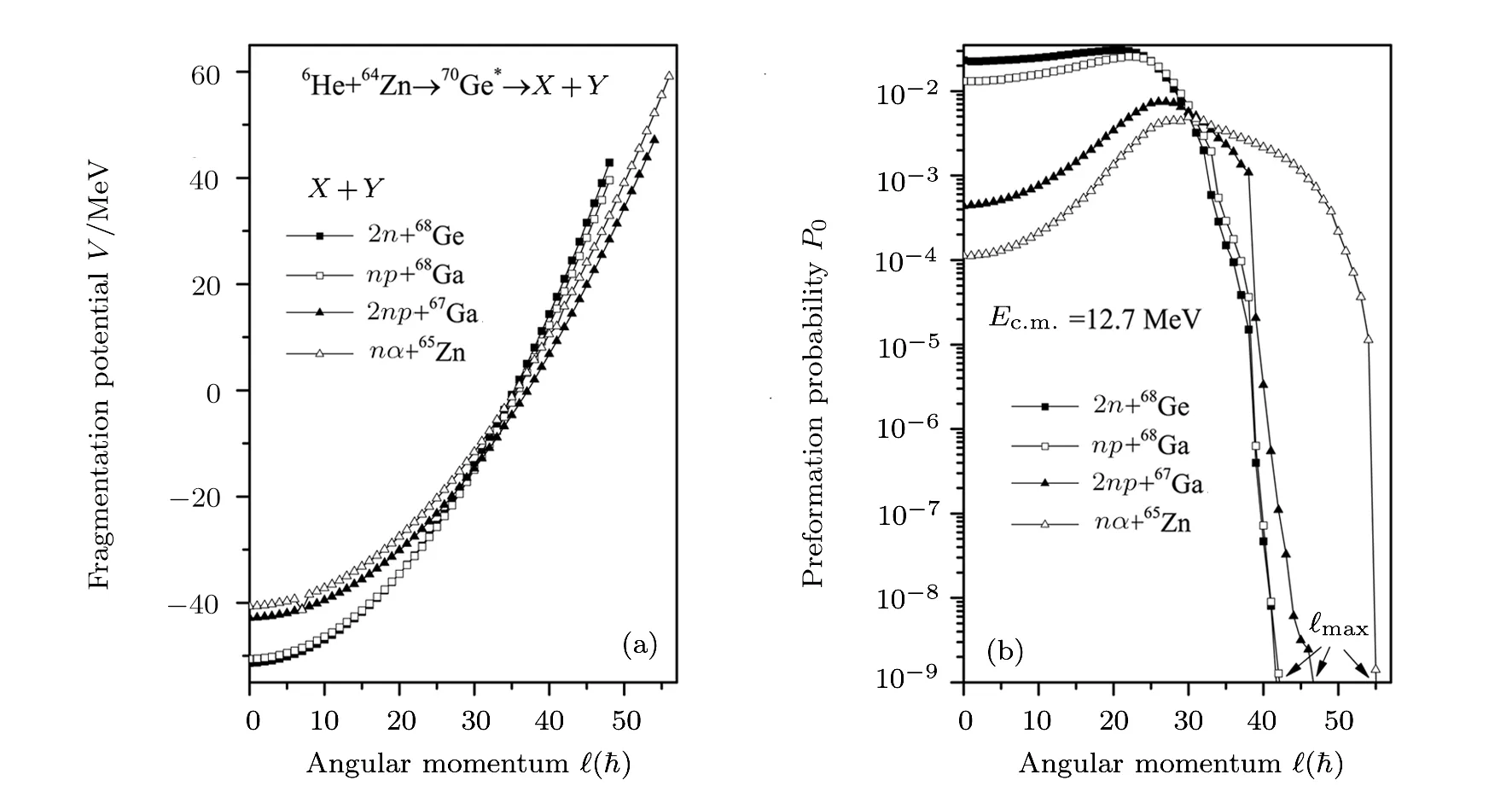
Fig.7 The fragmentation potential(V)and preformation probability P0vs.ℓ plotted for evaporation residues(2n)68Ge,(np)68Ga,(2np)67Ga and(nα)65Zn for the de-excitation of70Ge∗ system formed via using loosely bound nucleus as a projectile at energy 12.7 MeV.

Accordingly,the cross-sections are calculated for 1n decay of66Zn∗and 2p decay of68Ge∗via breakup and transfer reactions.The temperature(T)and best- fit∆R values are reported in Table 4 and both increase with increase in energy.The angular momentum contributing to the breakup+transfer cross-sections has the limiting valuesand.The total sum of DCM calculated breakup+transfer and fusion cross-sections show nice agreement with the experimental fusion data(refer Fig.9).Broadly speaking,the suppression in the total fusion cross-sections of70Ge∗CN due to nα and 2np channels is compensated through the breakup+transfer events leading to66Zn∗and68Ge∗nuclear systems,followed by 1n and 2p emission respectively.Conclusively,the loosely bound nature of the6He projectile influences the dynamics of6He+64Zn reaction as the total contribution of breakup+transfer channel is reasonably higher than that of the fusion cross-sections.

Table 3 The DCM calculated cross-sections for individual ER 2n,np,2np,and nα channels with best- fit values of∆R for the decay of70Ge∗at various centre-of-mass energies.obtained by summing all ERs cross-sections and compared with experimental fusion data.[21]

Table 3 The DCM calculated cross-sections for individual ER 2n,np,2np,and nα channels with best- fit values of∆R for the decay of70Ge∗at various centre-of-mass energies.obtained by summing all ERs cross-sections and compared with experimental fusion data.[21]

Ec.m.E∗CNT∆R2nσ2n(68Ge)∆Rnpσnp(68Ga)∆R2npσ2np(67Ga)∆Rnασnα(65Zn)σDCM fusσExpt.fus/MeV /MeV /MeV /fm /mb /fm /mb /fm /mb /fm /mb /mb /mb 7.54 30.20 2.036 1.592 9.97 - - - - 1.349 14.2 24.17 128.43 9.15 31.81 2.088 1.860 44.6 - - 1.433 3.37 1.447 18.7 66.67 283.07 10.60 33.26 2.133 1.980 70.1 1.890 106 1.700 16.2 1.650 32.8 225.1 501.08 11.83 34.49 2.171 2.140 116 1.980 139 1.910 34.0 2.020 53.8 342.8 553.85 12.70 35.36 2.197 2.300 165 2.070 174 2.120 55.1 2.070 51.7 445.8 809.01 13.80 36.46 2.230 2.306 164 2.030 150 2.350 72.9 2.150 49.0 435.9 817.81 15.00 37.66 2.266 2.300 153 2.170 209 2.400 72.2 2.200 45.9 480.1 863.29 16.10 38.76 2.298 2.260 141 1.965 114 2.430 71.5 2.250 42.0 368.5 781.04

Fig.8 Comparison of experimental cross-sections with calculated ones for(a)2n,(b)np,(c)nα,and(d)2np evaporation channels at various Ec.m.’s for the6He+64Zn reaction.

Finally,the comparison of4He+64Zn and6He+64Zn reactions is investigated in Fig.9.As mentioned above,the fusion cross-sections of nucleus formed in4He+64Zn reaction matches the experimental data nicely.On the other hand,suppression in the DCM calculated fusion cross-sections are observed for6He+64Zn reaction channel,due to mismatch in the cross-sections of nα and 2npclusters. If one compares the fusion cross-sections for4He+64Zn and6He+64Zn reactions,sub-barrier enhancement in the fusion cross-sections of6He+64Zn reaction is observed.However,the DCM fitted σfusfor6He+64Zn reaction bear lower magnitude at above barrier energies than the same calculated for4He+64Zn.These two results can be explained on the basis of structure properties of loosely bound projectile.The larger radius of the loosely bound projectile reduces the Coulomb barrier,as a result one can expect the fusion enhancement,as shown in Fig.9 at sub-barrier energies.

On the other hand,the low binding energy of the outer two neutrons of the6He nucleus implies large contribution of breakup+transfer channels,which could remove flux from the complete fusion and thus suppress the fusion cross-sections.The DCM results support that at the above-barrier energies,the loss of flux due to the breakup+transfer channels dominates and the resulting fusion cross-section is suppressed.Note that similar kind of results have been analyzed for the reactions of loosely bound projectile with heavy target(e.g.11Be+208Pb[7]).Hence from the above discussion the loosely bound nature of the6He can be easily illustrated by concluding following results:(i)The loosely bound character of the projectile is responsible for the breakup+transfer channels,which are addressed here through the two different breakup and transfer channels of6He i.e.2n+64Zn and4He+64Zn.(ii)The comparison of the tightly and loosely bound projectile induced reactions reveals the peculiar dynamics of6He+64Zn interacting pair.It has been emphasized that the loosely bound nature of6He is responsible for the sub-barrier fusion enhancement and above barrier fusion suppression.

Table 4 The calculated breakup+transfer cross-sections using DCM for 1n decay channel for 66Zn∗ excited system formed in the 2n+64Zn reaction,and 2p decay channel for68Ge∗ nucleus formed in4He+64Zn reaction at modified energies

Table 4 The calculated breakup+transfer cross-sections using DCM for 1n decay channel for 66Zn∗ excited system formed in the 2n+64Zn reaction,and 2p decay channel for68Ge∗ nucleus formed in4He+64Zn reaction at modified energies

Ecc.m./MeVE∗CN/MeVT/MeV∆R/fmσ/mb 2n+64Zn→66Zn∗→1n+65Zn 2.670 22.08 1.805 1.265 89 3.229 22.64 1.827 1.340 162 3.746 23.16 1.847 1.398 241 3.824 23.24 1.850 1.366 177 4.489 23.90 1.875 1.462 349 4.878 24.92 1.889 1.472 345 5.304 24.72 1.905 1.473 320 5.690 25.10 1.920 1.475 305 4He+64Zn→68Ge∗ → 2p+66Zn 9.470 12.82 1.370 1.570 17.5 10.30 13.65 1.412 2.060 76.0 11.05 14.40 1.448 2.450 112.0

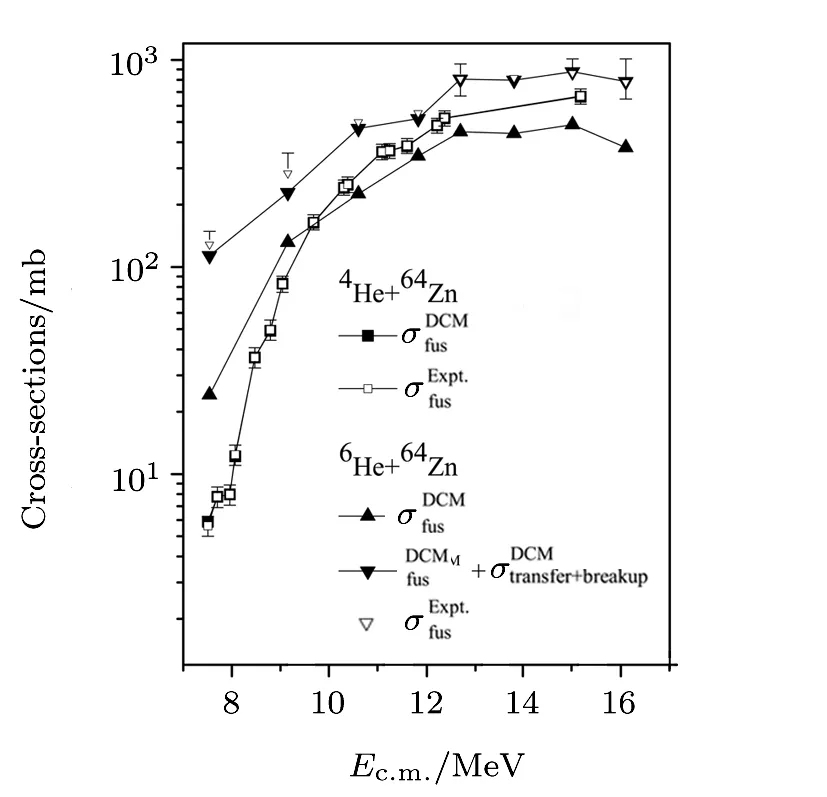
Fig.9 Variation of cross-sections as a function of centreof-mass energies for4He+64Zn and6He+64Zn reactions and compared with experimental data.[13,20−21]

4 Summary

In this work,we have investigated the decay of68Ge∗and70Ge∗nuclear systems formed via tightly bound“4He” and loosely bound “6He” projectiles over a wide range of center-of-mass energies Ec.m..The DCM calculated cross-sections find nice agreement with the experimental data for all the decay channels of68Ge∗nucleus.The p-and n-emissions,which are dominant decay modes of68Ge∗nucleus,show different barrier characteristics with respect to angular momentum(ℓ).Also,the Ec.m.-dependence and ℓ-dependence of fragmentation potential,preformation probability and barrier penetrability are duly addressed.Moreover,the fission contribution for the decay of68Ge∗has been predicted,which comes out to be negligibly small possibly due to lighter mass and lower excitation energies of compound system.Apart from this,another competing channel i.e.compound inelastic scattering is also analyzed at above barrier energies.

The excitation functions of various evaporation residues(ERs)(2n)68Ge,(np)68Ga,(2np)67Gaand(nα)65Zn for the decay of70Ge∗system are estimated and found that the σERfor(nα)65Zn and(2np)67Ga channel deviates from the experimental data.This deviation suggests the breakup of6He projectile(i.e.6He→2n+4He)and transfer of 2n and4He leads to the formation of66Zn∗and68Ge∗nuclei.The breakup+transfer cross-sections have been calculated by applying relevant energy corrections. The total sum of fusion and breakup+transfer cross-sections show nice agreement with experimentally measured fusion data.

Lastly,in order to understand the influence of the halostructure of6He,a comparative study of tightly bound“4He” and loosely bound “6He”projectile induced reactions has been carried out.A lower Coulomb barrier and smaller binding energy of loosely bound nucleus in turn influences the fusion cross-sections and related reaction mechanisms.Due to the loosely bound nature of6He nucleus,the sub-barrier enhancement and above-barrier suppression are observed in the fusion cross-sections of6He+64Zn reaction.