Convective Heat and Mass Transfer in Magneto Jeffrey Fluid Flow on a Rotating Cone with Heat Source and Chemical Reaction
2018-11-19SaleemAlQarniNadeemandSandeep
S.Saleem,M.M.Al-Qarni,S.Nadeem,and N.Sandeep
1Department of Mathematics,College of Sciences,King Khalid University,Abha,61413,Saudia Arabia
2Department of Mathematics,Quaid-e-Azam University,45320,Islamabad 44000,Pakistan
3Department of Mathematics,Central University of Karnataka,Kalaburagi-585367,India
AbstractThe present paper addresses the megnetohydrodynamic Jeffrey fluid flow with heat and mass transfer on an infinitely rotating upright cone.Inquiry is carried out with heat source/sink and chemical reaction effects.Further,constant thermal and concentration flux situations are imposed.Optimal homotopy analysis method(OHAM)is employed to achieve series solutions of the concerned differential equations.Important results of the flow phenomena are explored and deliberated by means of graphs and numerical tables.It is perceived that thermal boundary layer thickness possess contrast variations for the heat source and heat sink,respectively.The chemical reaction enhances the heat transfer rate but decline the mass transfer rate.Moreover,the precision of the existing findings is verified by associating them with the previously available work.
Key words:magnetohydrodynamics,Jeffrey fluid,rotational flow,heat generation/absorption,chemical reaction
1 Literature Survey
The worth of non-linear fluid is obvious due to its enormous applications in countless industrial and manufacturing areas.This phenomenon realizes great importance in academic as well as in applied perspective.Heat and mass transfer in Non-Newtonian liquids are correspondingly crucial in food processing,substantial oils and greases.[1−6]An important area of study is mixed convection flows,which occurs in atmospheric boundary layer flows,heat exchangers,nuclear reactors and in electrical tools.More recent developments are canister’s structure for nuclear waste disposal,nuclear reactor cooling system.Anilkumar and Roy[7]achieved the similar solution for time dependent flow in rotational cone.Raju[8]has measured the impacts of the thermophoresis on radiative combined convection on a rotational cone with porousity.Sulochana et al.[9]explored numerical study of MHD flow by a roatating cone with nanoparticles and chemical reaction.Nadeem and Saleem[10]deliberated a theoretical analysis for MHD flow above a spinning cone.The flow over conic shape objects has been studies by various investigators.[11−12]
The phenomena of megnetohydrodynamics(MHD)flows with convectional heat and mass transfer is significant in technological and industrial applications.Saleem et al.[13]explored an unsteady water-based nanofluid flow besides an upright rotating cone with buoyancy effects.Sheikholeslami[14]investigated impact of Coulomb forces on Fe3O4H2O nanofluid. Sheikholeslami and Ganji[15]studied inspiration of MHD flow of CuO-H2O nanofluid seeing Marangoni boundary layer.Sandeep et al.[16]presented unsteady flow of thermophoric MHD nanomaterial by stretching surface with internal heat source/sink.Sheikholeslami and Ellahi[17]discussed three dimensional microscopic model of natural convection flow of nanofluid with magnetic particles.Sparrow and Cess[18]presented MHD flow and heat transfer around a rotational disk.In nature,most of the flows are unsteady due to the ambient velocity.So,as a step just before the consequential progress of study on mixed convection flows,it is very significant and valuable to study such flows about an upright cone with the heat and mass diffusion,while the ambient velocity fluctuates randomly with time.Together with thermal and mass transfer,chemical reaction is of worth in numerous developments.Chemical reaction are revealed as any homogeneous or heterogeneous procedures.It is based on wether it takes place at a boundary or as a single point volume.A homogeneous reaction arises in particular phase.The species generation in a homogeneous reaction is the parallel to the inner cause of heat generation.On contrary,other reaction happens in a controlled region or with in the phase boundary.Similarly,numerous physical existences include free convection determined by heat generation.[19−21]The vision for performed analysis is to explore the impact of heat generation/absorption and chemical reaction on MHD Jeffrey fluid in a spinning cone.The extremely nonlinear partial differential equations prescribed by heat flux situations are transmuted into structure ordinary differential equations with suitable constraints and then answered by the optimal homotopy analysis method(OHAM).[22−35]Likewise,the impact of interesting parameters on the velocities,surface stress tensors,temperature and concentration fields are discovered and deliberated through graphs and numerical columns.The accuracy of the analytical technique is also confirmed by comparing the results with existing literature.
2 Mathematical Analysis
Consider an incompressible,axisymmetric Jeffrey fluid flow about a cone.The flow is unsteady due to the rotation of cone.
A rectangular curvilinear coordinate system is engaged in which,x is along tangential direction,y is in azimuthal direction,and z is in normal direction to the cone axis Fig.1.Additional u,v,and w are the velocity components in the tangential,azimuthal and the normal directions,respectively.A continuous magnetic field is utilized perpendicular to the cone.Induced magnetic field is absent for small magnetic Reynolds number.

Fig.1 Geometry of the flow field.
Further electric field is absent.After using the Boussinesq approximations,the boundary layer motion,energy and diffusion equations for a Jeffrey fluid are given as.[7,10]

λ1is the ratio of relaxation and retardation times and λ2is the retardation time.Presenting the suitable nondimensional quantities:[7]


At this point s is the unsteadiness parameter;the flow field is assisting for positive s and vice versa.λ1is the buoyancy force parameter,N is the fraction of the buoyancy forces and mass diffusion,A is the Deborah number.The incompressibility equation(1)is identically fulfilled and Eqs.(2)to(5)take the form:
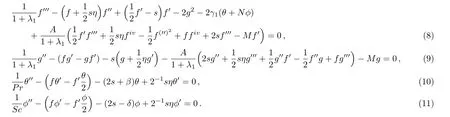
The boundary conditions for the flow problem in non-dimensional form are stated as follows:

The skin friction coefficients in x and y directions are correspondingly set as
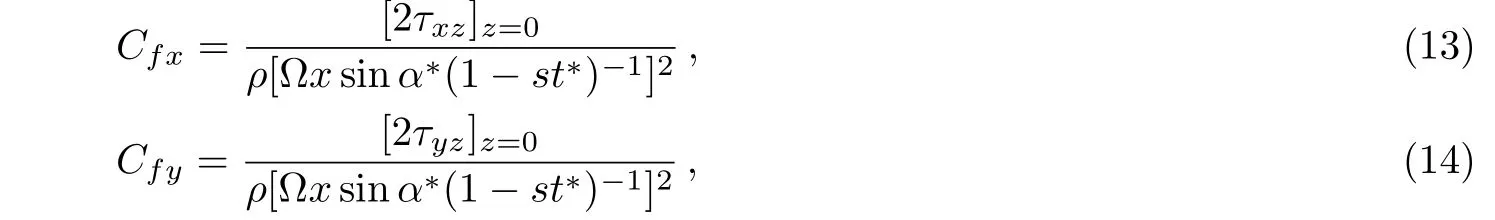
or
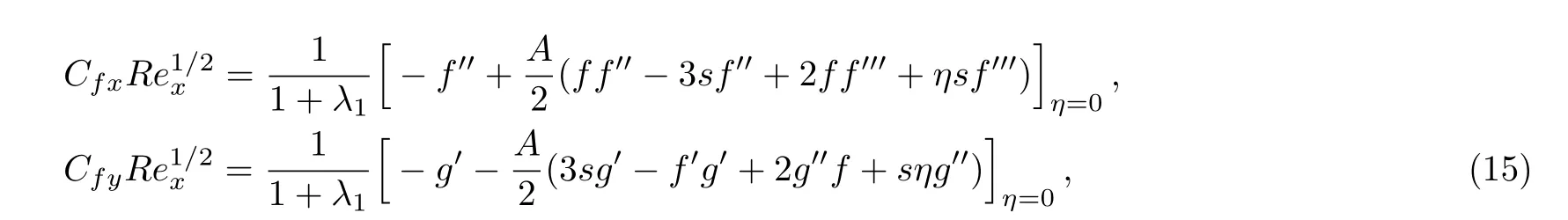
where
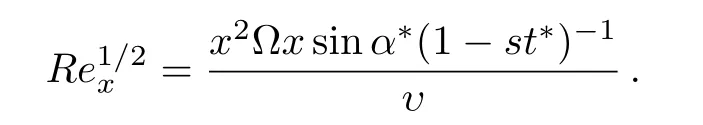
The heat and mass transfer rates are respectively given by:

3 Solution Expressions
The highly nonlinear Eqs.(8)to(12)are treated with optimal homotopy analysis method[].The initial guesses f0,g0,θ0,ϕ0as follows:


3.1 Optimal Convergence-Control Parameters
The auxiliary parameters which are involved in the convergence of the homotopic solutions areandWe have engaged the notion of minimization by introducing the residual errors to find out the optimum values ofandas introduced by Ref.[20].

Table 1 Optimal convergence control parameters and total averaged squared residual errors using BVPh2.0.
The Mathematica package BVPh2.0 is used to minimize the average residual error.Three arrays of total optimum convergence control parameters are attained at 2nd,4th,and 6thiterations(see Table 1).
With 4thiteration optimum convergence-control parameter,singular averaged squared residual errors is achieved and offered in Table 2.Averaged-squared residual errors and total averaged-squared residual errors are reduced by increasing the approximations.

Table 2 Individual averaged squared residual errors using optimal values at m=8 from Table 1.
4 Analysis of Results
In order to deliberate the inspiration of numerous physical constraints on the velocity field,thermal boundary layer,skin-friction,Nusselt number and sher wood number,the analytical solution is obtained in the above segment,has been carried out and shown graphically.The regime is controlled by thermo-physical parameters,which are ratio of buoyancy force N,Deborah number A and ratio of the relaxation to the retardation time λ1,the unsteadiness parameter s,the magnetic parameter M,Prandtl number Pr and schmidt number Sc.

Fig.2 Impact of M on tangential velocity −f′(η).

Fig.3 Impact of M on azimuthal velocity g(η).
4.1 Dimensionless Velocities
In Figs.2 and 3 the evolution of dimensionless tangential and azimuthal velocities inside the boundary layer,against span wise coordinate η for magnetic parameter M is shown.It is perceived that the force exerted by magnetic field opposes both velocities,f′(η)and g′(η).It is also observed that the both velocities attain greater magnitude for s<0.
4.2 Dimensionless Temperature
It is illustrated from Fig.4 that temperature of the fluid reduces its magnitude for heat source coefficient β>0 when unsteadiness parameter s>0.While the behaviour is reverse when s<0.Further temperature decreases more rapidly for s>0.The impact of heat sink parameter β<0 on parameter filed is demonstrated in Fig.5.As expected,the graphical variation is opposite when compared with Fig.4.
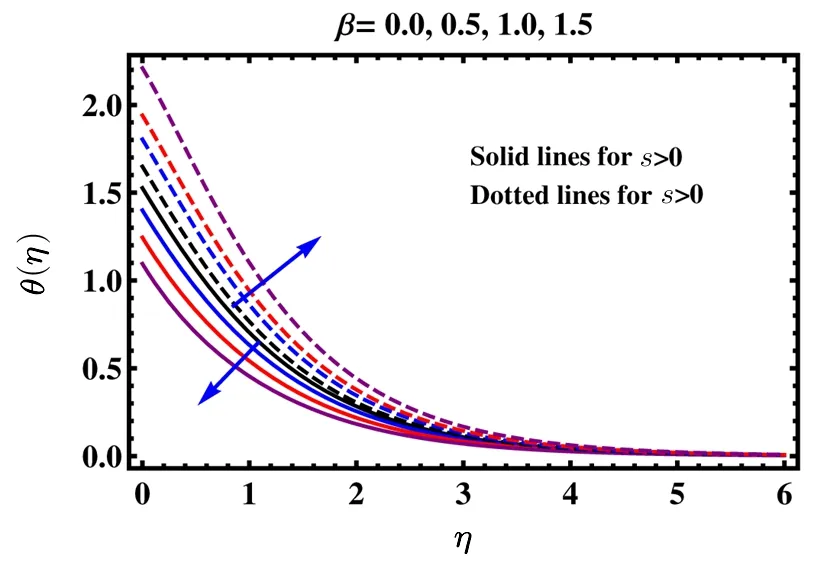
Fig.4 Impact of β >0 on temperature θ(η).
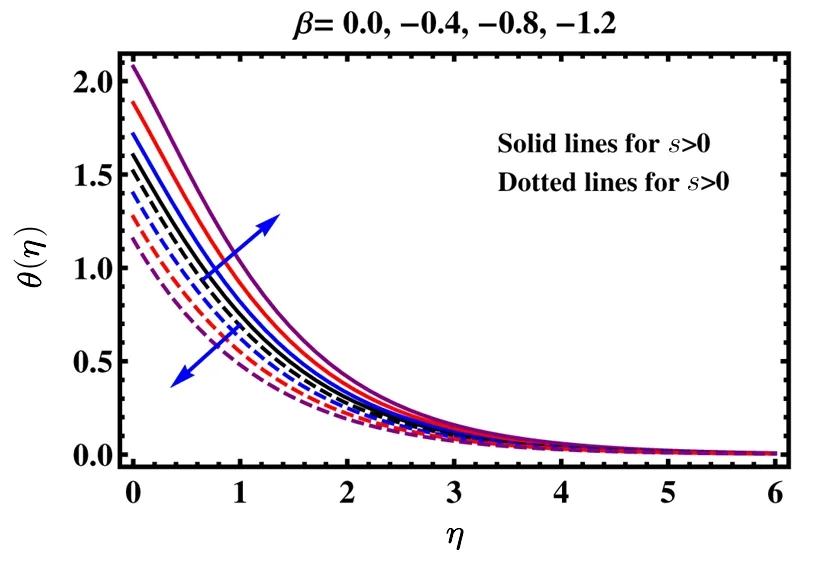
Fig.5 Impact of β ≤ 0 on temperature θ(η).
4.3 Dimensionless Concentration
Figure 6 exhibits the effect of δ on the concentration filed.It is depicted that concentrated field is an accumulative function of δ for every value of s.Since chemical reaction consequences the consumption of the compound of concern and hence concentration field indicates reduction.Besides the concentration boundary layer thickness has higher magnitude for s<0.The inspiration of β and δ on local Nusselt number is offered in Figs.7 and 8 correspondingly.It is revealed from Fig.7 that the increase in β causes reduction in the local Nusselt number,but after of s=0 its magnitude goes higher.While local Nusselt number enhances its variation along with δ(see Fig.8).Figure 9 is devoted to see the deviations of the local Sherwood number for several values of chemical reaction δ.It is of a great interest that local Sherwood number decreases due to a rise in δ.In addition,to verify the stability of present results,comparison Tables 3 and 4 is computed in the lack of buoyancy force and heat generation/absorption parameter with the results set by sparrow and Cess.[18]The results are seen to in the decent compatible order with each other.

Fig.6 Impact of δ on concentration pro files ϕ(η).

Fig.7 Impact of β on local Nusselt number.
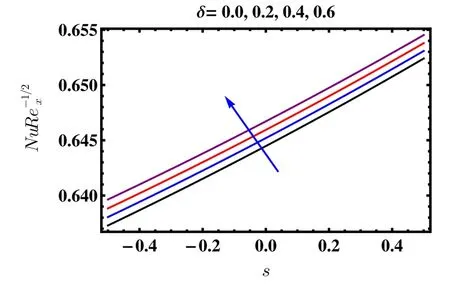
Fig.8 Impact of δ and s on local Nusselt number.
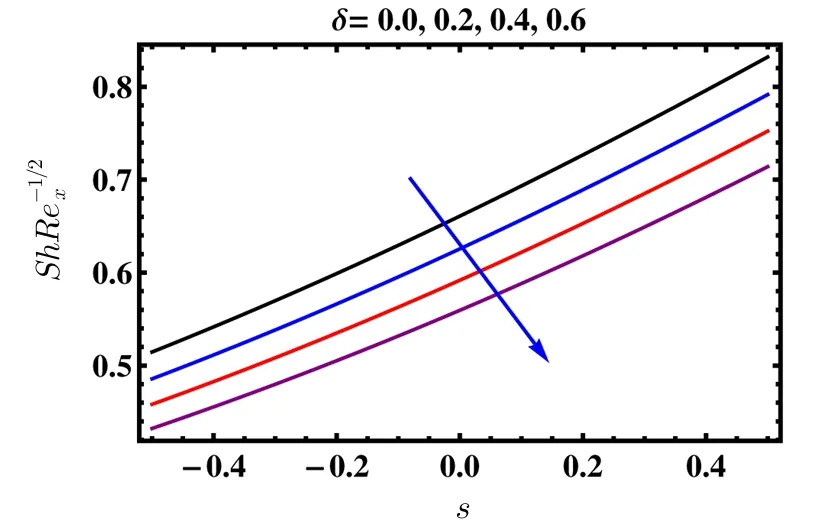
Fig.9 Impact of δ and s on local Sherwood number.

Table 3 Comparitive results for significant physical numbers for special case.
4.4 Skin Friction Coefficients
Table 5 is prepared for values of skin friction coefficients against A and λ1,M, γ1s,and N.It is obvious that tangential skin friction coefficient escalates with larger values of A,γ1s,and N,but decreases with λ1and M.Besides this,azimuthal skin friction coefficient has a direct relation with all these pertinent parameters.It is due to the information that wall temperature at the cone boundaries is rather larger than the temperature of the fluid which finally rises the Gγ1as compare to Gγ2,thus greater value of N offer the larger values of skin friction coefficients.

Table 4 Comparitive results of heat transfer rate for limiting case.

Table 5 Skin friction coefficient for selected significant constraints.
4.5 Nusselt and Sherwood Numbers
The effect of Pr,Sc,and N on heat and mass transfer rate coefficient is deliberated in Table 6.It is found that Pr and N improve the heat transfer rate coefficient while the variation is opposite for Sc.Physically the fluid with greater Prandtl number has a lesser thermal conductivity,which effects in thinner thermal boundary layer and as an outcome rate of heat transfer increases.Also the mass transfer rate coefficient demonstrate a growing apptitude for different values of N and Sc.On the contrast,Pr reduces the magnitude of mass transfer rate coefficient.
5 Key Points
In the current analysis,the behaviour of MHD Jeffrey fluid flow with heat source and chemical reaction on a rotational vertical cone is investigated.The non-dimensional differential equations with heat and mass flux conditions are solved with well supposed analytical procedure known as optimal homotopy analysis method(OHAM).The recently considered outcomes are recognized to be in conventional settlement with the earlier printed results.It is observed that heat source β >0 and heat sink β <0 possess opposite variations for temperature field.The role of δ is to the enhancement of concentration field.The tangential skin friction coefficient varies as an inverse function of λ1.The impact of M is to decrease the tangential skin friction coefficient whereas increases the azimuthal skin friction coefficient.
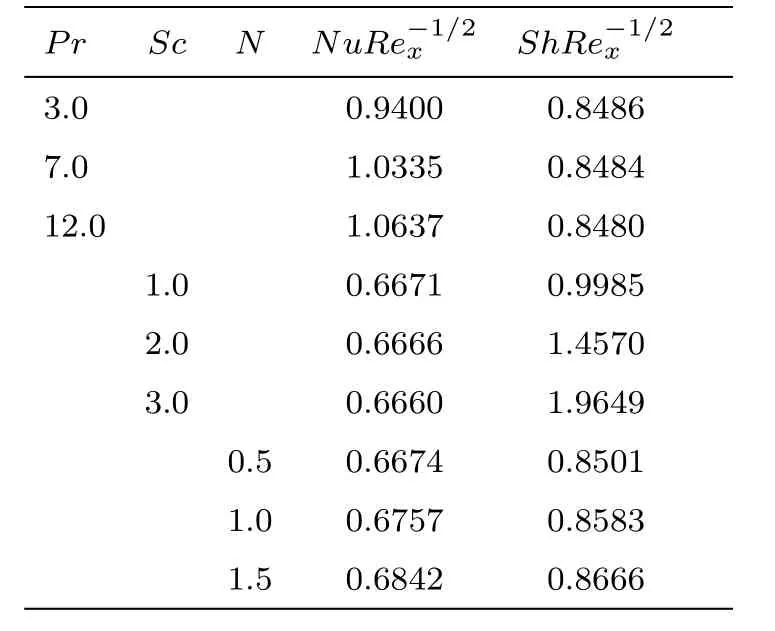
Table 6 Local Nusselt and Sherwood numbers for certain noteworthy physical parameters.
Acknowledgement
The authors would like to express their gratitude to King Khalid University,Abha 61413,Saudia Arabia for providing administrative and technical support.
杂志排行
Communications in Theoretical Physics的其它文章
- Optical Solitons and Stability Analysis in Ring-Cavity Fiber System with Carbon Nanotube as Saturable Absorber
- Scheme for Asymmetric and Deterministic Controlled Bidirectional Joint Remote State Preparation∗
- Lump and Stripe Soliton Solutions to the Generalized Nizhnik-Novikov-Veselov Equation∗
- A Practical E-Payment Protocol Based on Quantum Multi-Proxy Blind Signature∗
- Scattering and Bound States of the Dirac Particle for q-Parameter Hyperbolic Pöschl-Teller Potential
- Probing Nonclassicality of Two-Mode SU(2)Generator Based on Quantum Fisher Information∗
