Lump and Stripe Soliton Solutions to the Generalized Nizhnik-Novikov-Veselov Equation∗
2018-11-19ZhengYiMa马正义JinXiFei费金喜andJunChaoChen陈俊超
Zheng-Yi Ma(马正义), Jin-Xi Fei(费金喜),and Jun-Chao Chen(陈俊超)
1Institute of Nonlinear Analysis and Department of Mathematics,Zhejiang Lishui University,Lishui 323000,China
2Department of Mathematics,Zhejiang Sci-Tech University,Hangzhou 310018,China
3Department of Photoelectric Engineering,Zhejiang Lishui University,Lishui 323000,China
AbstractWith the aid of the truncated Painlevé expansion,a set of rational solutions of the(2+1)-dimensional generalized Nizhnik-Novikov-Veselov(GNNV)equation with the quadratic function which contains one lump soliton is derived.By combining this quadratic function and an exponential function,the fusion and fission phenomena occur between one lump soliton and a stripe soliton which are two kinds of typical local excitations.Furthermore,by adding a corresponding inverse exponential function to the above function,we can derive the solution with interaction between one lump soliton and a pair of stripe solitons.The dynamical behaviors of such local solutions are depicted by choosing some appropriate parameters.
Key words:Nizhnik-Novikov-Veselov equation,quadratic function,rational solution,lump soliton,stripe soliton
1 Introduction
The(2+1)-dimensional Korteweg-de Vries(KdV)equation introduced by Boiti et al.can be expressed[1]
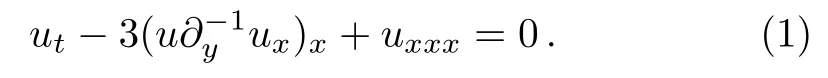
This nonlocal equation reduces to the(1+1)-dimensional KdV equation

if x = y. The generalized Nizhnik-Novikov-Veselov(GNNV)equation is a symmetric generalization of the(2+1)-dimensional KdV equation
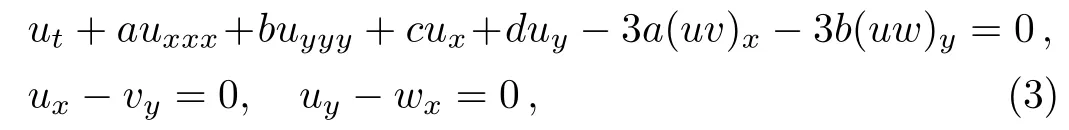
where a,b,c,d are four free constants and Eq.(3)is also an isotropic Lax integrable extension of the(1+1)-dimensional KdV equation.This equation has been shown to be completely integrable and poessess exponentially localized solutions.[2−3]Using a novel approach involving the truncated Laurent expansion in the Painlevé analysis,the constructed multi-elliptic function solutions and multi-dromions have been extended to the trilinearized case of GNNV equation.[4]The elementary and systematic binary Bell polynomials method has been applied to this equation.[5]The bilinear representation,bilinear Bäcklund transformation(BT),Lax pair and infinite conservation laws of this equation have been obtained directly,without too much trick like Hirota’s bilinear method.Applying the truncated Painlevé expansion to the(2+1)-dimensional asymmetric Nizhnik-Novikov-Veselov(ANNV)system,some BTs including auto and non-auto ones have been obtained.[6]Starting from the consistent tan-function expansion(CTE),some complex interaction solutions between soliton and arbitrary other seed waves of the ANNV system have constructed,such as bight-dark soliton solution,dark-dark soliton solution,soliton-cnoidal wave interaction solutions,solitoff solutions and so on.
One of valid ways to describe nonlinear phenomena is to derive various kinds of explicit solutions in the appropriate physical models,such as typical solitons and traveling wave solutions in nonlinear science.Recent advances in integrable systems,computer technics and numerical approaches have brought the development of effective techniques to search for these solutions.These powerful approaches include the inverse scattering method(a method which can be used to solve the initial value problem for certain classes of nonlinear partial differential equations),[7]the bilinear method(a new stability-preserving order reduction approach),[8]the Bäcklund transform(which is typically a system of first order partial differential equations relating two functions,and often depending on an additional parameter).[9]The typical methods also include the truncated Painlevé expansion,[10]the similarity reduction,[11]the hyperbolic function method[12]and so on.
This paper is presented as follows.In Sec.2,starting from the truncated Painlevé expansion,a set of rational solutions of(2+1)-dimensional GNNV equation with the quadratic function which contains a lump soliton is derived.In Sec.3,by combining the quadratic function with an exponential one,the interaction phenomena with fusion and fission between a lump and one stripe solitons are presented.In Sec.4,by introducing an inverse exponential function further for the above function,one generalized solution including the stripe soliton pairs interacting with a lump is obtained.The dynamical behaviors of such local solutions are discussed by choosing the appropriate parameters.The last section is a short summary.
2 Lump Soliton Solution
A lump soliton structure is localized in both space directions and described in a fully developed rogue wave(RW)which can be expressed by one suitable rational function.[13]For this purpose to the GNNV equation(3),we need the following process.The truncated Painlevé expansion[14−15]of Eq.(3)is

here f is the singularity manifold,ui,vj,wk(i,j,k=0,1,2)are related to the function f as well as its derivative,which can be determined by substituting Eq.(4)into Eq.(3).Through the computation of fourteen overdetermined equations of these functions,the truncated Painlevé expansion can be derived
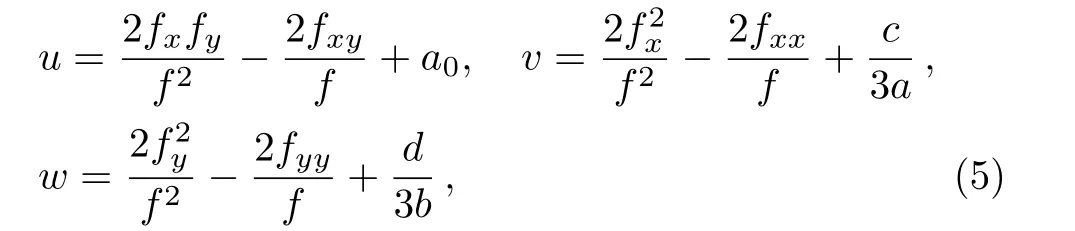
here a0is a real constant.
To search for the lump and its corresponding structures,we need to take the following quadratic function f,which has been proved effectively to the Kadomtsev-Petviashvili(KP)-like equations[16−23]
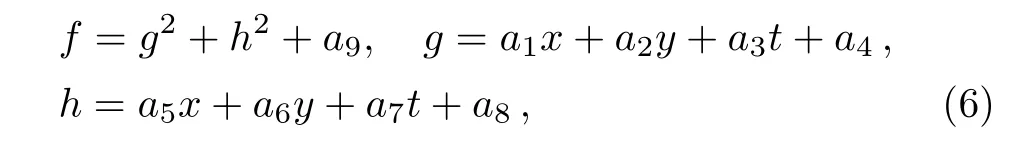
where ai(i=1,2,...,9)are nine undetermined real parameters.By substituting Eq.(6)with(5)into Eq.(3)and collecting the coefficients of the variables x,y,and t,one can get twenty equations.A direct calculation leads to the following algebraic relation

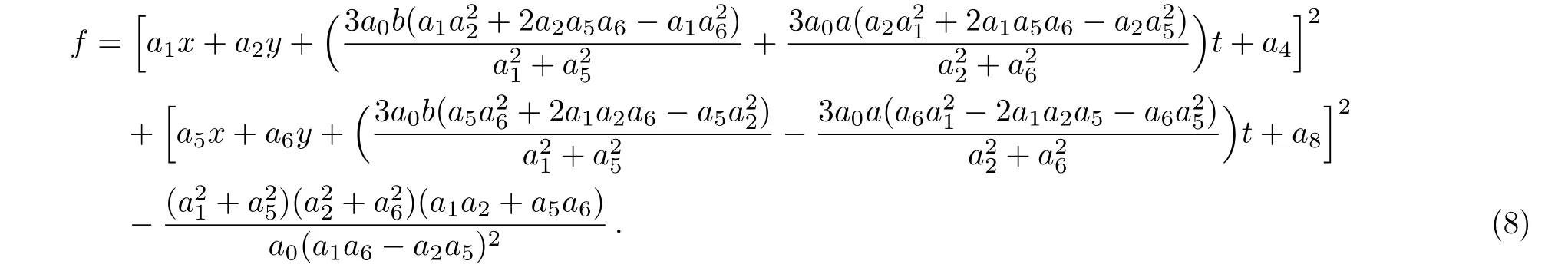
Therefore,the corresponding solution of the(2+1)-dimensional integrable GNNV equation(3)reads
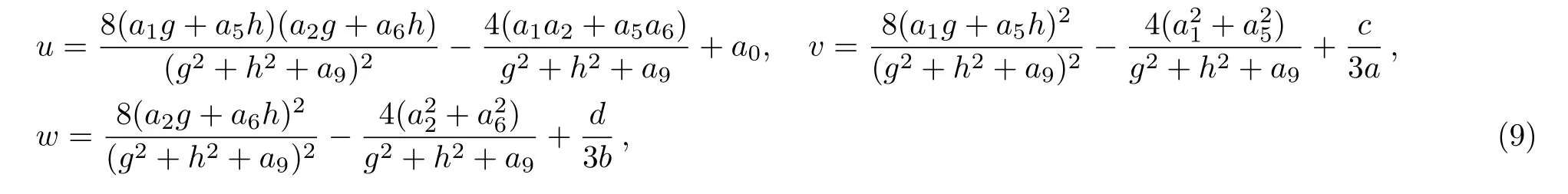
with
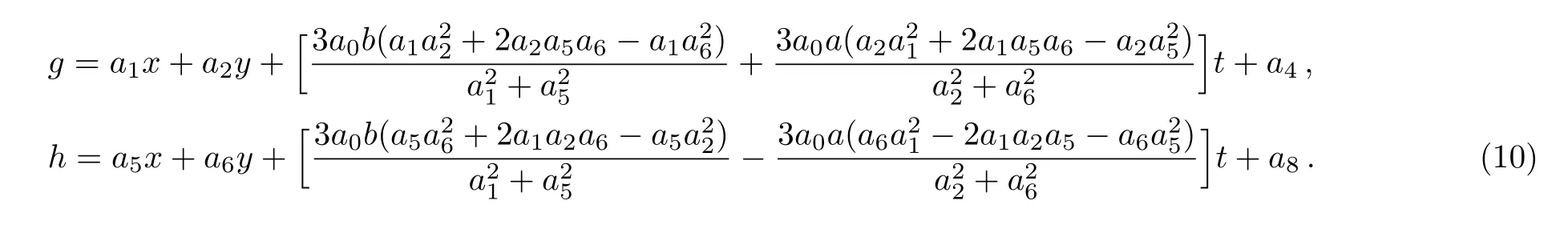
Although the parameters a1,a2,a4,a5,a6,and a8are arbitrary,the solution should be well defined,which means two columns(a1,a2)and(a5,a6)out of proportion and unparallel in the(x,y)-plane,and the lump soliton solution could be taken shape.For this case,it can be seen from Eq.(9)that the lump solution tends to 0 at any given time t whenor equivalently,The moving path of this lump can be depicted by
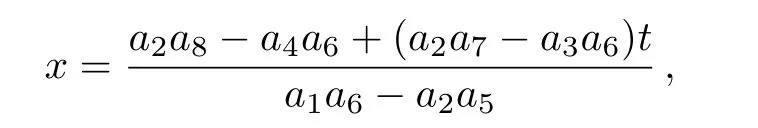

from vx=vy=0 of Eq.(9).This indicates its moving velocity
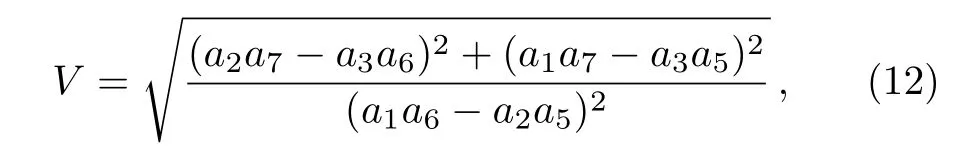
and the maximum amplitude
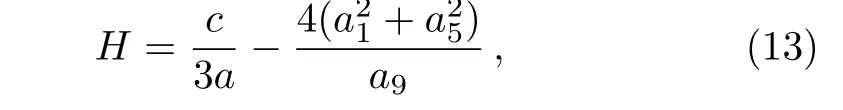
along with the moving path

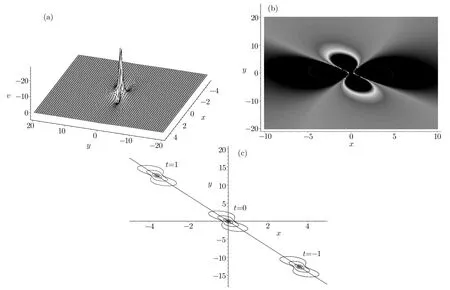
Fig.1 Pro files of the solution v in Eq.(9)with the time t=0,(a)3D lump plot,(b)the corresponding density plot,respectively.(c)The contour plot with routing display.
As a typical example,we choose the parameters a=b=c=d=a2=a5=1,a0=a1=2,a4=a8=0,a6= −1,so a3= −27/5,a7=81/5,a9=5/9.The conditionsandare guaranteed,one lump solution is shown explicitly in Fig.1 for the solution v of Eq.(9).The chosen parameters a4=a8=0 affirm the lump with center at the origin when t=0.The corresponding moving velocity,the maximum amplitude and the moving path of this lump areandrespectively,which can be derived from Eqs.(12)–(14).Figure 1(a)is the three-dimensional plot of this lump at time t=0,Fig.1(b)is the corresponding density plot.Figure 1(c)shows contour plot of the lump at different times−1,0,1 and the moving route as described by the straight line at the slope−7/2 in the(x,y)-plane.
3 Interaction Solution Between One Lump Soliton and a Stripe Soliton
This section is to describe the interaction between one lump soliton and a stripe soliton with fusion and fission phenomena.Generally speaking,the elastic collision between solitons in an integrable model is one of the most important phenomena in soliton theory which means the velocity,amplitude and wave shape of each soliton do not change after their interaction.[24−25]However,in some special circumstances,the interactions between soliton excitations such as peakons and compactons of some integrable models are not completely elastic.[26]In particular,two or more solitons may fuse into one while one soliton may fission into two or more.Such phenomena are often called soliton fusion and fission.[27−28]Indeed,these phenomena have been found in many physical fields like plasma physics and hydrodynamics.[29−30]
In the following,we seek for the fusion and fission phenomena for the(2+1)-dimensional integrable GNNV equation(3).By adding the exponential function
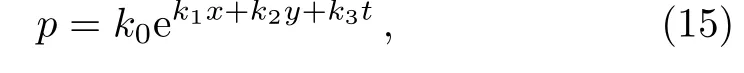
to Eq.(6)with k0,k1,k2,and k3being four undetermined real parameters,the function f is expressed by
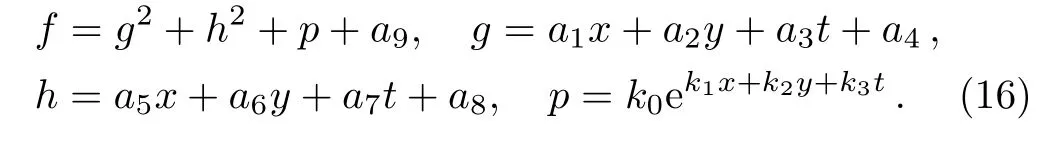
Substituting Eq.(16)with Eq.(5)into Eq.(3)and collecting the coefficients of the variables x,y,t leads to 65 equations.By solving these equations,we obtain the following constraint relations of the parameters
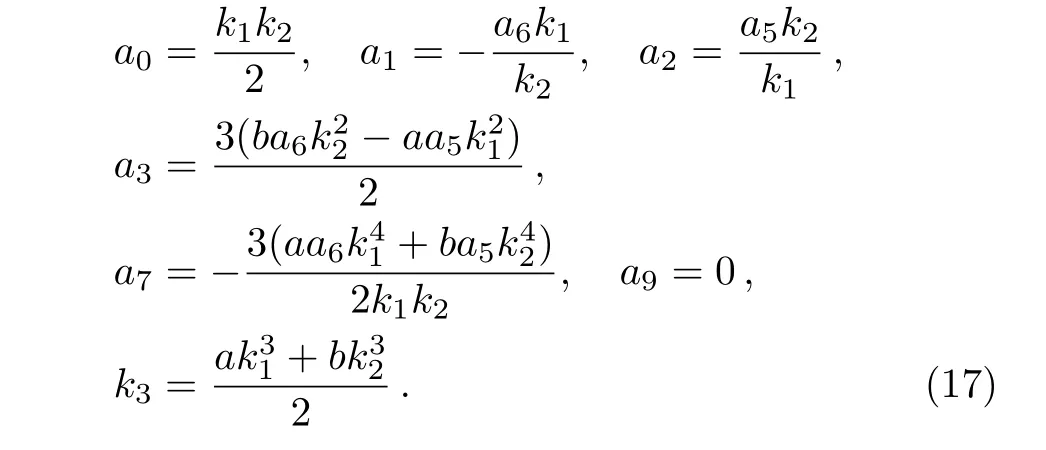
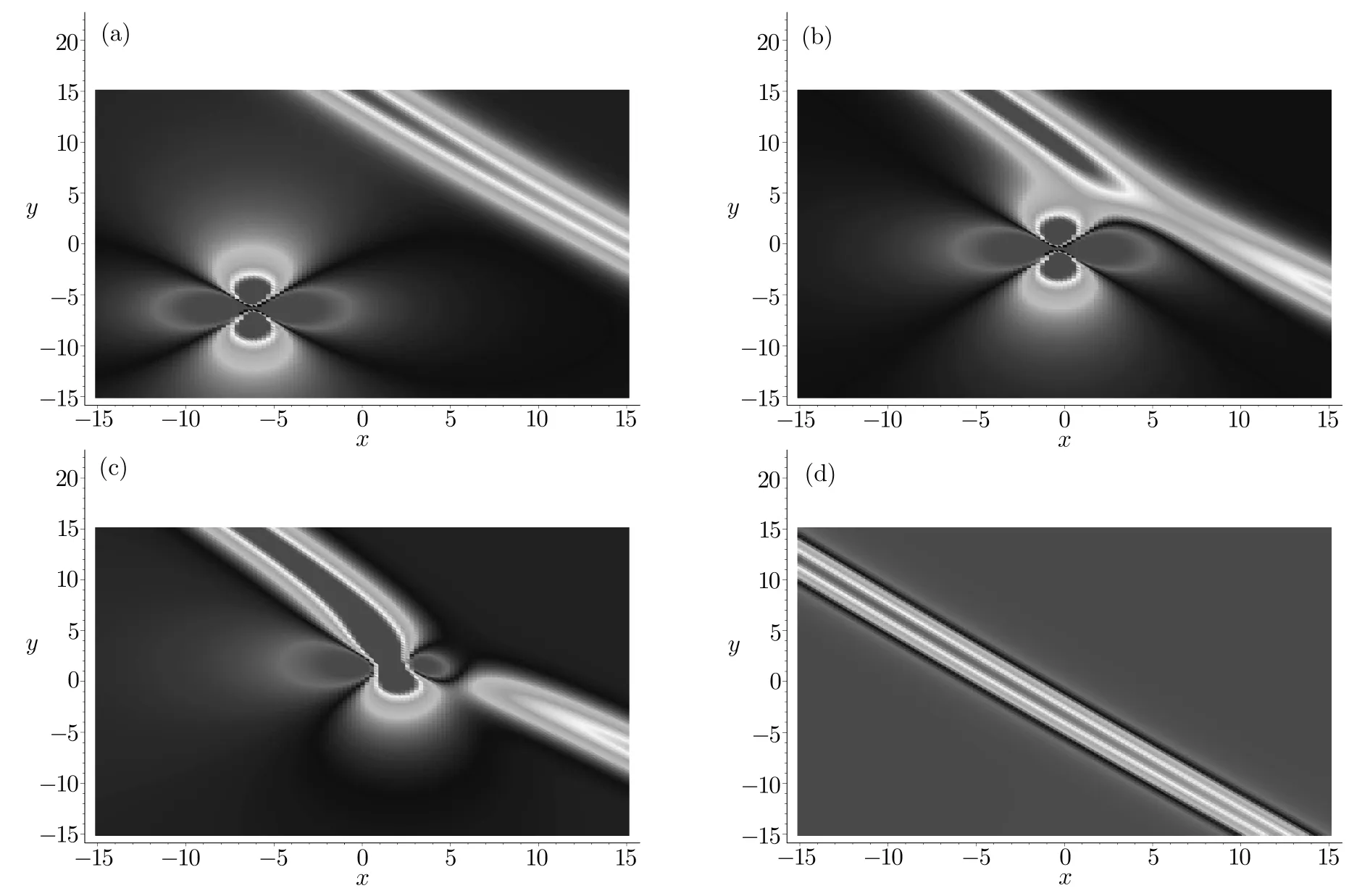
Fig.2 Density figures of the fusion solution v in Eq.(19)between one lump soliton and a stripe soliton with the times t= −4,−0.1,1.5,15,respectively,in(x,y)-plane with the parameters(21).
In this situation,the quadratic function solution of Eq.(16)is taken as
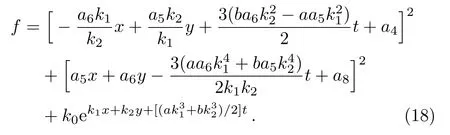
Then the corresponding solution of the GNNV equation(3)has the form
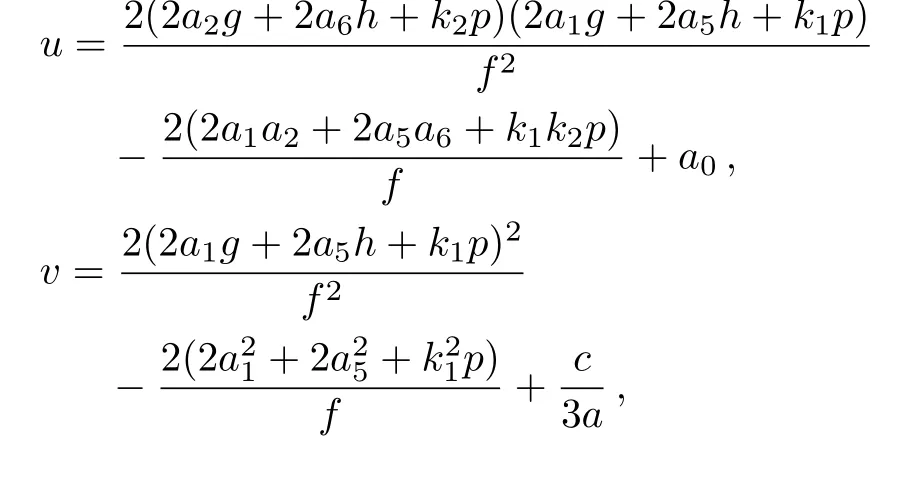

with
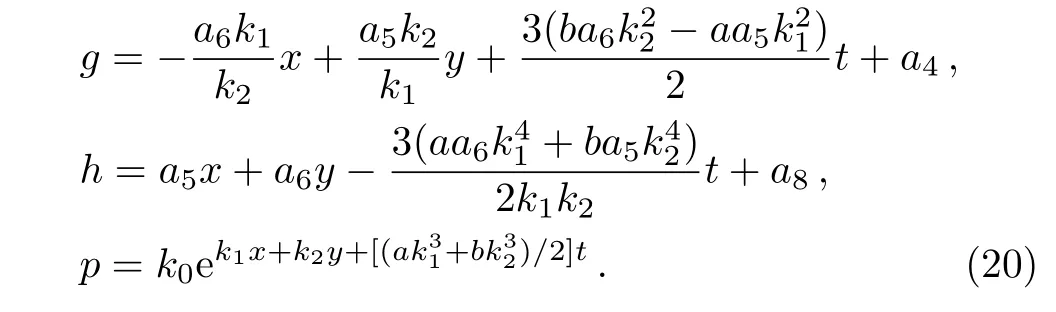
The above constraint relations of the parameters(17)need to ensure the localization of the solution u,v,w. To obtain the interaction solution between one lump soliton and a stripe soliton to the integrable GNNV equation,we consider the special circumstance of the above solution(19)and(20)when a9=0.
The above solution(19)is a composition of the quadratic sum of two polynomial functions g,h and an exponential function p for the variables x,y,t,and obviously,the order of an exponential function is higher than the polynomial functions.To illustrate the fusion and fission interaction structures,we choose the following values of related parameters
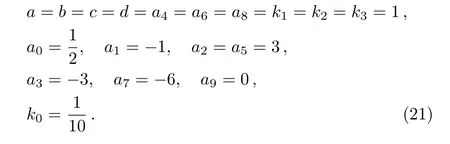

Fig.3 Density figures of the fission solution v in Eq.(19)between one lump soliton and a stripe soliton with the times t= −15,−2,0.1,4,respectively,with the parameters(21)except for the opposite values of a2,a3,a5,a7,k1,k2,k3.
Figures 2(a)–2(d)show the whole fusion process between one lump soliton and a stripe soliton as they move in same direction.Figure 2(a)shows one lump and a stripe soliton in the separate station at the time t=−4.When t=−0.1,the lump has chased after and tangled with the stripe as shown in Fig.2(b).Then,this lump begins to be swallowed by the stripe as shown in Figs.2(c)(t=1.5)and 2(d)(t=15),and its energy transfer into the stripe soliton gradually,until these two solitons blend into one stripe structure.On the contrary,when some parameters are taken just the opposite values,i.e.a2=a5=−3,a3=6,a7=3,k1=k2=k3=−1,but the rest are the same as above(21),the fission phenomenon occurs only if the time t is taken from −15 to 4.Figures 3(a)–3(d)show the whole fission process between one lump soliton and a stripe soliton.
4 Interaction Solution Between One Lump Soliton and Stripe Soliton Pairs
Along with the idea of the collision of one lump soli-ton and a stripe soliton,we start to study the collision of one lump soliton with stripe solitons pairs.To this end,we continue to add the exponential function which is a inverse one of Eq.(15)in the form

to the expression of the function f in Eq.(16),where n0is also an undetermined real parameter.Then Eq.(16)has the form Substituting Eq.(23)with Eq.(5)into Eq.(3),after the complicated calculation,we have


Fig.4 Density figures of the interaction solution v in Eq.(25)between one lump and stripe soliton pairs with the symmetric time t= −20,−1,0,1,20,respectively,with the parameters(29).
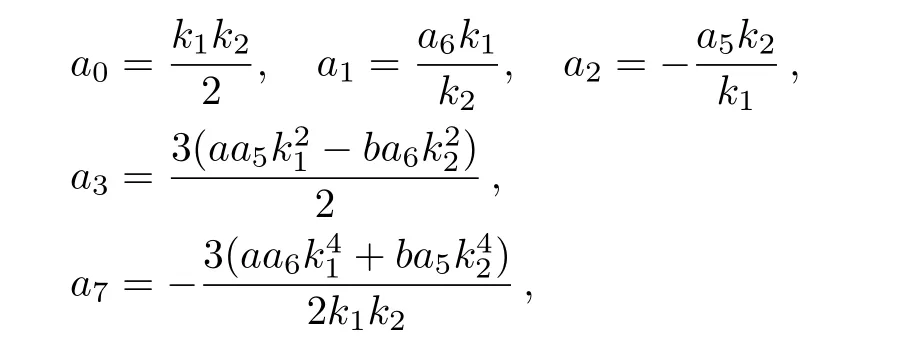
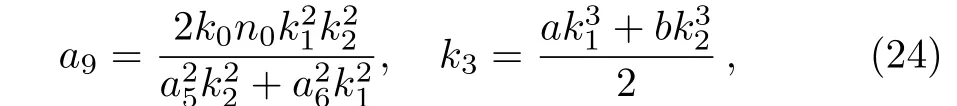
where the rest parameters may take arbitrary real constants theoretically if and only if the above expression(24)is meaningful.Then the corresponding rational solution of the(2+1)-dimensional integrable GNNV equation
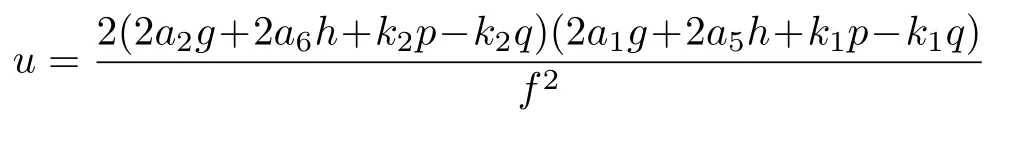
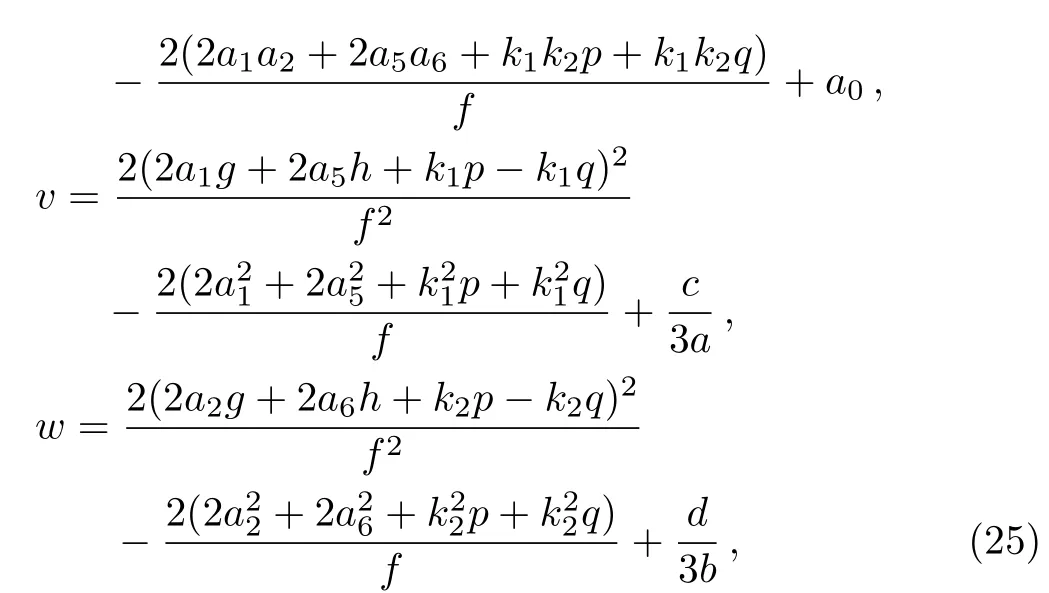
with
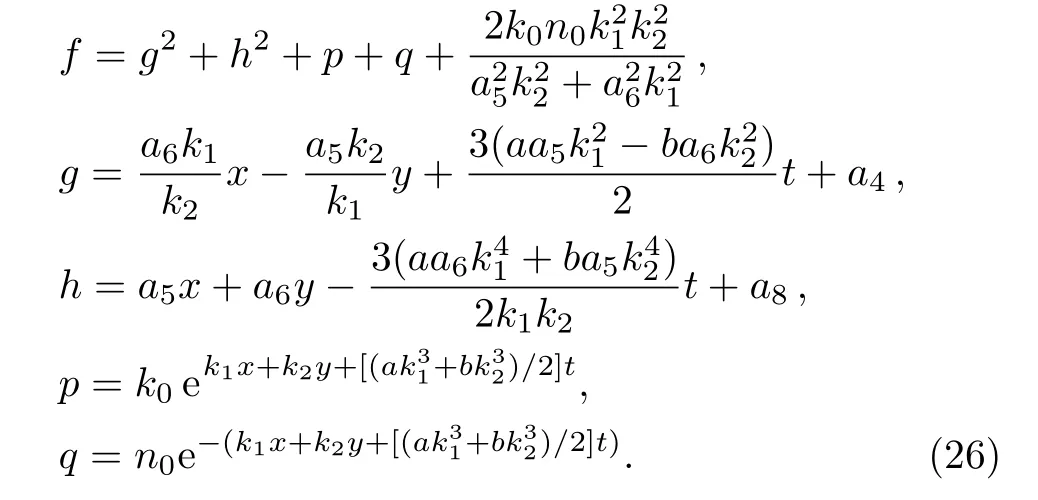
The asymptotic behavior of one lump and resonance soliton pairs can be studied according to the expression of Eq.(26).By taking
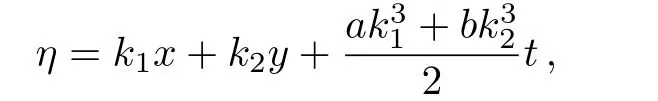
it is found that the function relation of g and η reads

and further the limited relations for g,h and p+q are given by

The expression(28)implies that two polynomial functions g,h are the same order,while the exponential function p+q is higher than a polynomial function when the time t→±∞.At this time,the resonance solitons pairs arise,since g in Eq.(27)contians the scaling and time displacement for η under the condition of η being a constant.
In order to illustrate such an interaction effect,we choose the parameters as
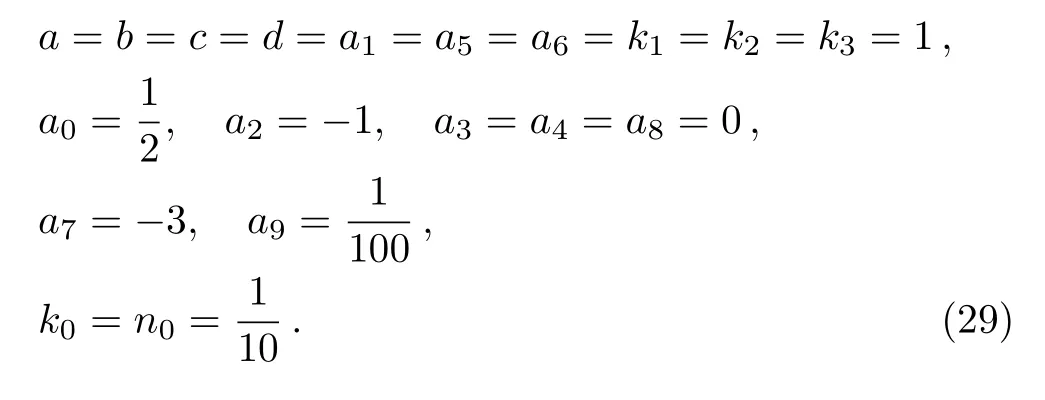
Figures 4(a)–4(e)show the interaction solution between one lump soliton and stripe soliton pairs at times t= −20,−1,0,1,20,respectively,in(x,y)-plane.Figure 4(a)exhibits the resonance soliton pairs,in which a lump soliton is merged in the left one and almost invisible.With the increase of the time t,this lump fission from the left stripe propagating in Fig.4(b).At the moment t=0,the amplitude of lump arrives at the maximum,a lump and stripe soliton pairs are separated explicitly.Figures 4(c)and 4(d)show that the lump begins to be swallowed by the right stripe soliton,until the lump fuse into this stripe and continues to move in the same direction.
5 Conclusion and Summary
The study of the lump dynamic behaviors for the nonlinear GNNV equation firstly starts from the truncated Painlevé expansion with an auxiliary function f.By taking the auxiliary functions as the special form including the quadratic function and exponential function,we derive the lump solution,the interaction solution among one lump,a stripe soliton,and stripe soliton pairs.The lump solution is characterized by its structure localizing in all directions in the space.By combining the quadratic function with an exponential one,the interaction phenomena with fusion and fission between one lump and a stripe solitons are presented.For the interaction among one lump and a stripe soliton,there are two different physics phenomena:fusion and fission.In the process of fusion,the lump soliton and stripe soliton are independent from each other at first and as time goes on,lump soliton begins to be swallowed gradually until disappearing.The fission is an inverse progress of the fusion.As is known to all,to find the fission/fusion of the local coherent structures in a(2+1)-dimensional integrable equation is an important task.Furthermore,by introducing an inverse exponential function for the established function,one generalized solution including the stripe soliton pairs interacting with a lump is obtained.The dynamical behaviors of such local solutions are discussed mainly in density forms by choosing the appropriate parameters.
Indeed,in nonlinear science,the studying of the explicit solution about an integrable system is helpful in clarifying the underlying algebraic structure of the soliton theory and plays an important role in reasonable explaining of the corresponding natural phenomenon and application.These related localized excitations and their behaviors are originated from many natural sciences,such as fluid dynamics,plasma physics,solid physics,superconducting physics,condensed matter physics and optical problems.[31−34]In fact,it is of interest to study such types of analytical solutions.As we know,the soliton and solitary wave are two typical nonlinear structures widely appearing in many physical fields such as ocean.Here we mainly devote to obtain the interaction of lump and stripe soliton solutions from the original model equation.It is expected to the realistic physical interpretation and experiment observation.For instance,in recent work,[35]the oblique propagation of ion-acoustic soliton-cnoidal waves was reported in a magnetized electron-positron-ion plasma with superthermal electrons.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects∗
- Hierarchical Human Action Recognition with Self-Selection Classifiers via Skeleton Data∗
- Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer∗
- Third-Order Magnetic Susceptibility of an Ideal Fermi Gas∗
- Coherent Control of the Hartman Effect through a Photonic Crystal with Four-Level Defect Layer∗
- Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas∗
