二维立体匹配模型及其数值解法

王春艳，朱华平，胡鹏辉

武汉理工大学 理学院，武汉 430070

1 引言

立体匹配是计算机视觉领域的重要研究课题之一，其主要目的是获取立体图像对的空间相同点坐标，进而从二维图像获取空间场景的深度信息并进行三维重建。目前，该领域的研究热点和难点之一是，提出适用于左右匹配点不全在同一条极线上，即极线校准不精确问题的通用模型[1]，以及如何克服该模型对应能量泛函中数据项的非凸性，避免陷入局部最优，进而得到全局最优解的方法。云挺等[2]利用极线考虑立体图像对匹配点在不同相对位置下的数据项，适用于几乎所有的图像对，对提出的能量泛函应用梯度下降法求解。但是该模型需要计算极线方程，且使用的算法容易陷入局部最优，在迭代过程中还需要对图像对进行插值计算。因此这种模型难以广泛应用，特别是在设备参数未知的情况下。Rudin等[3]提出连续全变分正则化模型，为克服该模型数据项的非凸性，Pock等[4-5]引入未知函数的示性函数，将原变分问题改写为高一维空间中的凸问题，然后利用对偶公式表示为鞍点问题，最后利用原始对偶近似点的方法求全局最优解，避免了用欧拉法求解全变分出现分母为零的情况。然而该模型仅能计算一维视差的情况，意味着仅考虑了左右匹配点极线在水平线上的情况。

本文重点研究了二维立体匹配模型及其数值解法。基于标准的笛卡尔理论，将二维立体匹配模型表示为四维空间上的变分问题。与一维模型不同的是，二维模型标准化后仍是非凸的，因此需要对非凸性变分问题的数据项进行松弛。利用对偶理论中的双共轭函数对其进行对偶化，改写为二维原始对偶立体匹配模型。基于该模型与鞍点结构优化模型的相似性，从而使用一阶原始对偶算法[6]求解该模型。

2 模型的建立

2.1 一维立体匹配模型

一维立体匹配模型[3]可以表述为下面的变分问题：

其中u:Ω→A是未知函数；Ω⊆R2表示图像区域；是函数u的取值范围；x=(x,y)T表示图像坐标。假定函数u满足第二边界条件。

式（1）的第一项表示正则项，用来平滑解u。第二项表示数据项，其值表示在点x处当视差值为u时的匹配代价。

模型（1）对应的离散形式为：

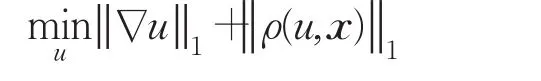
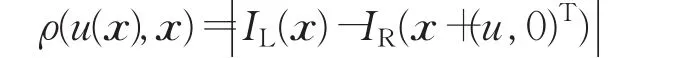
在文献[4]中，利用未知函数的示性函数对模型进行凸表示：

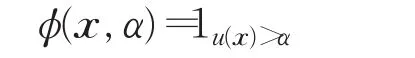
得到与一维模型（1）等价的高维问题：

然后利用对偶公式，得到等价的鞍点问题：

上述对偶模型的离散形式为：

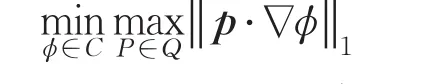
之后利用原始对偶近似点算法[7]进行求解。

2.2 二维立体匹配模型

传统的立体匹配模型通常是在一个维度上进行搜索，对立体图像对校准精度要求很高，当达不到这个要求时，得到的视差图像精度不高。为能处理这个问题，在一维模型中加入另一维度的视差搜索函数，得到变分问题：

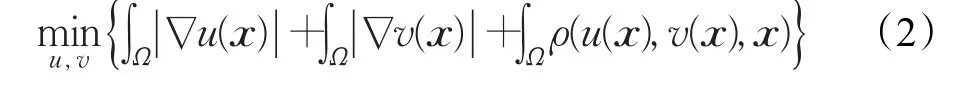
模型（2）对应的离散形式为：

不难看出，一维模型的视差仅由x方向视差决定，二维模型的视差由x、y两个方向的视差决定，考虑了极线校准不精确情况，可以处理匹配点在任意相对位置的情况。

3 模型的凸表示

本文将对提出的二维模型进行凸表示，使之成为鞍点问题。首先利用标准的笛卡尔理论改写二维立体匹配模型（2）为高维空间中的变分问题。然后利用双共轭函数，对正则项和数据项分别进行对偶表示。

定义1二值函数定义为：

易知φ、φ的可行集为：

上面定义了如何由u、v得到φ、φ。反过来，若已知 φ、φ，可由式（7）、（8）得到 u、v：

上面是关于u、v和φ、φ的关系。接下来将用φ、φ来表示变分问题（2），目的是把变分问题改写为凸的变分问题。

首先使得变分问题在凸集范围内求解，也就是要把φ、φ可行集（5）、（6）凸松弛，得到：

定理1变分问题（2）等价于高维的变分问题：

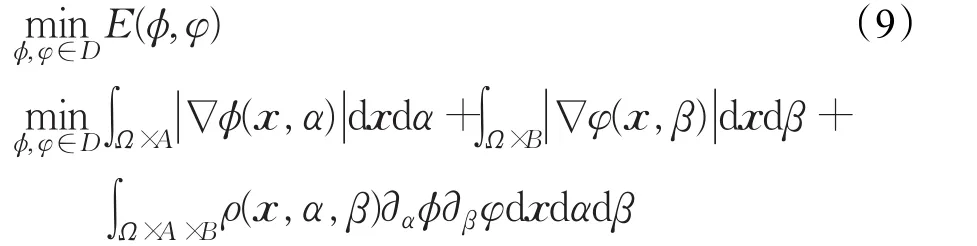
变分问题（9）最优解可以通过式（7）、（8）表示为变分问题（2）的最优解。

证明首先问题（2）正则项可以分别由φ、φ表示，利用推广的Co-area公式，得到：

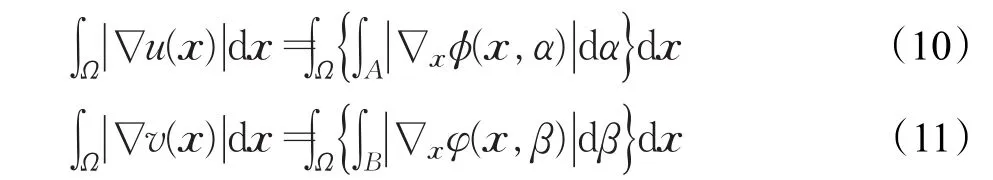
这里∇x表示仅对3自变量函数进行x的梯度运算。

其次用 φ、φ 改写问题（2）数据项，从式（3）、（4）可得。求解φ、φ在变量α、β的导数，则有：

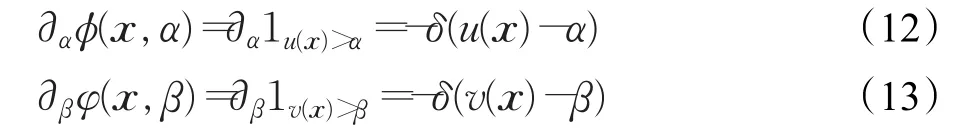
将式（10）、（11）、（14）代入变分问题（2）便可得到定理1。证毕。

与一维变分问题不同的是，这里变分问题（9）仍为非凸的，求解模型得不到最优解。关于其非凸性有如下结论。

性质变分问题（9）关于φ、φ是凸的，当且仅当对于任意点 (φ,φ),(ξ,ψ)∈D ，有(φα-ξα)⋅(φβ-ψβ)≥0 。

证明能量泛函（9）是凸的，也就是对任意的θ∈[0,1]，有下式成立：

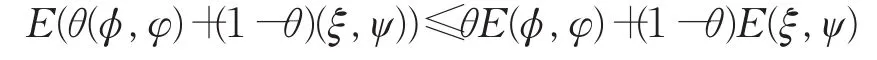
由于梯度算子及1范数的凸性，上式等价于：

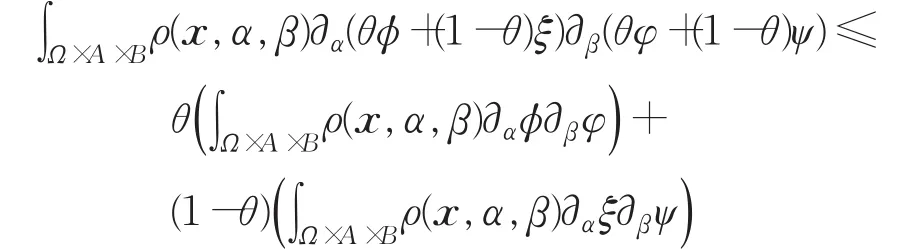
也就是对任意点 (x,α,β)∈Ω×A×B 满足 (φα-ξα)⋅(φβ-ψβ)≥0。上述为等价条件。证毕。

易知，关于变分问题凸的充要条件不是自然成立的。因此将对数据项进行凸松弛[8-9]，用其双共轭函数来近似。首先对双共轭函数[10-13]进行说明。

函数 f(x)关于x的Legendre-Fenchel共轭函数为：

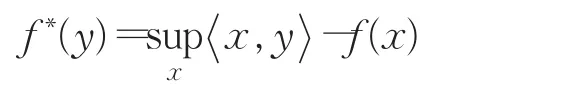
函数 f(x)关于x的Legendre-Fenchel双共轭函数为：

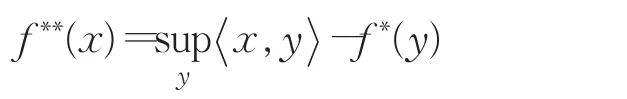
若 f(x)关于 x 是凸的，则 f∗∗(x)=f(x)；否则，f∗∗(x)是 f(x)的最小凸包（凸包络）。

定理2变分问题（9）的最小凸包为：

其中

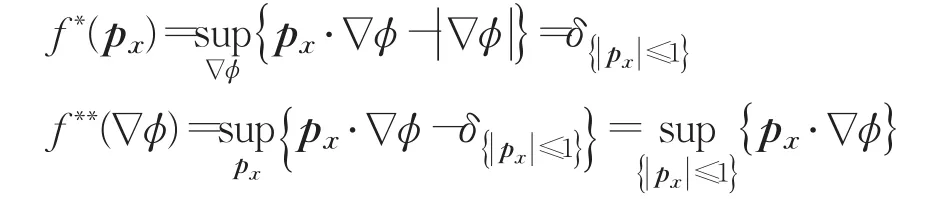
其次，对于数据项进行对偶化的处理。由性质可知，数据项是非凸的，因此用双共轭函数仅仅可以得到最小凸包。若数据项表示为：

则其共轭函数为：

由Dirac Delta函数的性质可知，若u(x)=a,v(x)=b,则有：

数据项的双共轭函数为：

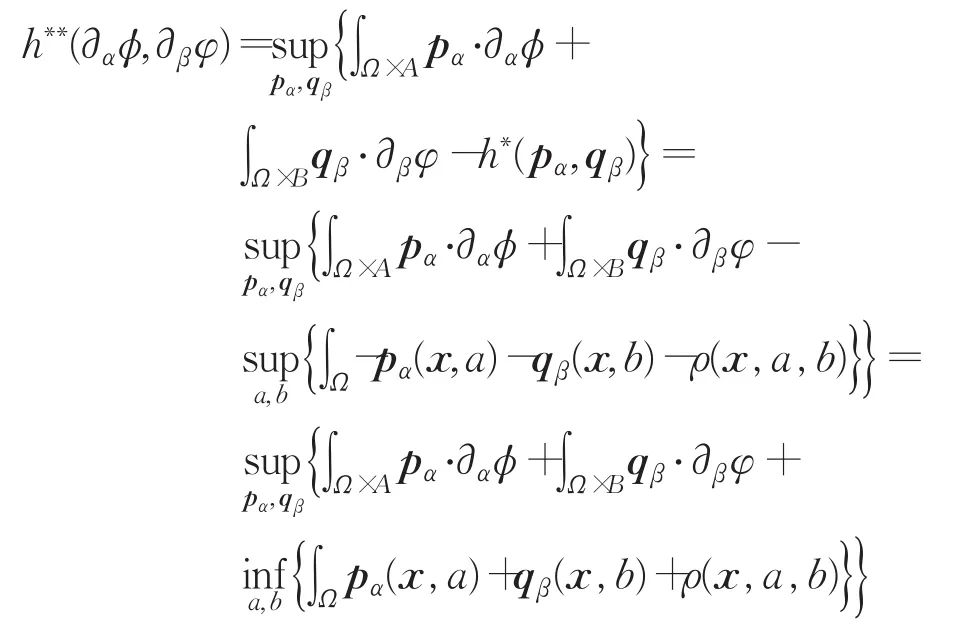
为使上式成立且计算简便，使得下式成立：

上式成立的一个条件便是：

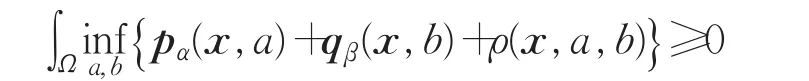
即对任意的 x、α、β，有：

若满足上述条件（16），则有：

把对偶变量 p、q满足的条件整合，则有定理集合G成立，把正则项和数据项代入变分问题（9）则有定理成立。证毕。

上述对偶模型的离散形式为：

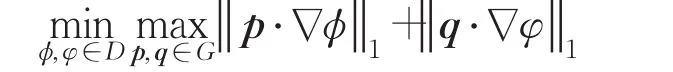
其为典型的鞍点问题，接下来将对该问题进行求解。

本文的最终目的还是解决二维变分问题（2），下面说明怎样由凸松弛后变分问题得到的最优解得到变分问题（2）的最优解。假设松弛后变分问题的最优解为φ∗、φ∗，通过下式得到：

要注意的是，这里u、v并非变分问题（2）的最优解，仅仅是在一定范围的次最优解。

不难看出，这里已经建立鞍点问题（9）与模型（2）的对应关系，即鞍点优化模型与二维立体匹配模型的对应关系。

从二维模型（2）的定义以及其等价的鞍点形式可知，当其中y方向视差v=0，二维模型就变为一维模型，与二维模型等价的鞍点问题也变为与一维模型等价的鞍点问题。由此可以得出，二维模型是一维模型的推广。

4 模型的原始对偶算法

文献[6]提出了一阶原始对偶算法，用来解决鞍点结构的优化问题。因此可以直接得到关于凸松弛后变分问题（15）的算法，如下所示。

算法1

（1）初始化：选取可行集 D×G 中变量 (φ,φ)×(p,q)，且令，迭代步长为 τ,σ＞0 且满足

（2）迭代：

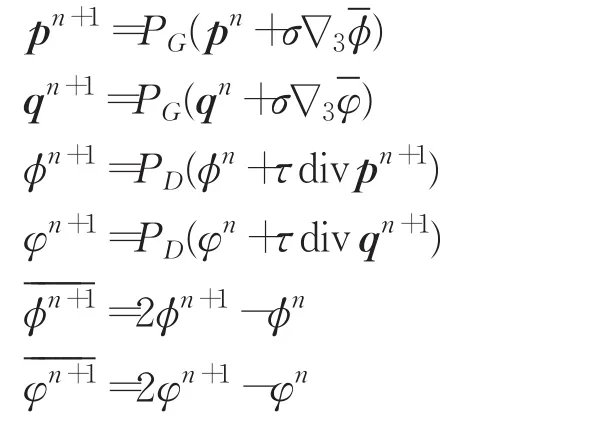
（3）计算能量泛函（2）的值，当迭代的能量差小于给定的阈值停止迭代；否则，令n=n+1，转（2）。

算法1中P表示投影算子，PD是向集合D投影，PG是向集合G投影。原始变量集投影算子PD用简单的截断函数实现。对偶变量集PG用下式进行投影运算，关于x有：

关于 pα、qβ的投影就是求下述最优问题，对于每点x,α,β∈Ω×A×B有：

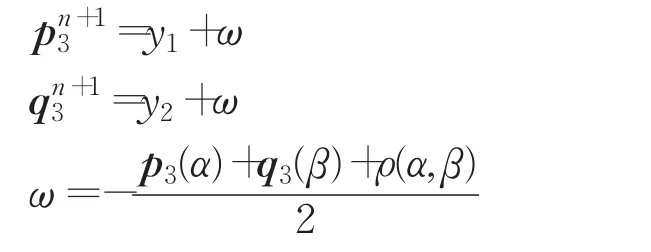
本文中梯度算子用向前差分进行近似，散度算子用向后差分进行近似。因此关于初始化迭代步长关系式中，梯度算子的范数为‖‖∇=12。

5 实验结果与分析

为测试并评价本文算法，在Matlab 2017a平台上，对文献[14]提供的Middlebury立体视觉2014版数据库中15种场景的1/4像素双目图像进行实验，并对实际获取的真实场景图像进行了求取视差的实验与结果分析，采用一维模型[2]和本文的二维模型进行比较。

5.1 标准库实验结果

用全部标准库中的立体图像对进行测试。表1给出本文结果与一维立体匹配在Middlebury网站的测评结果。本文给出两种误差，分别为非遮挡误匹配率（nocc，%）和所有区域误匹配率（all，%），误差阈值为1，并且给出了算法运行时间的对比。实验数据中存在关于亮度变化的立体图像对，对于有光照影响的图像对采用文献[15]中的关于梯度的匹配代价作为数据项。

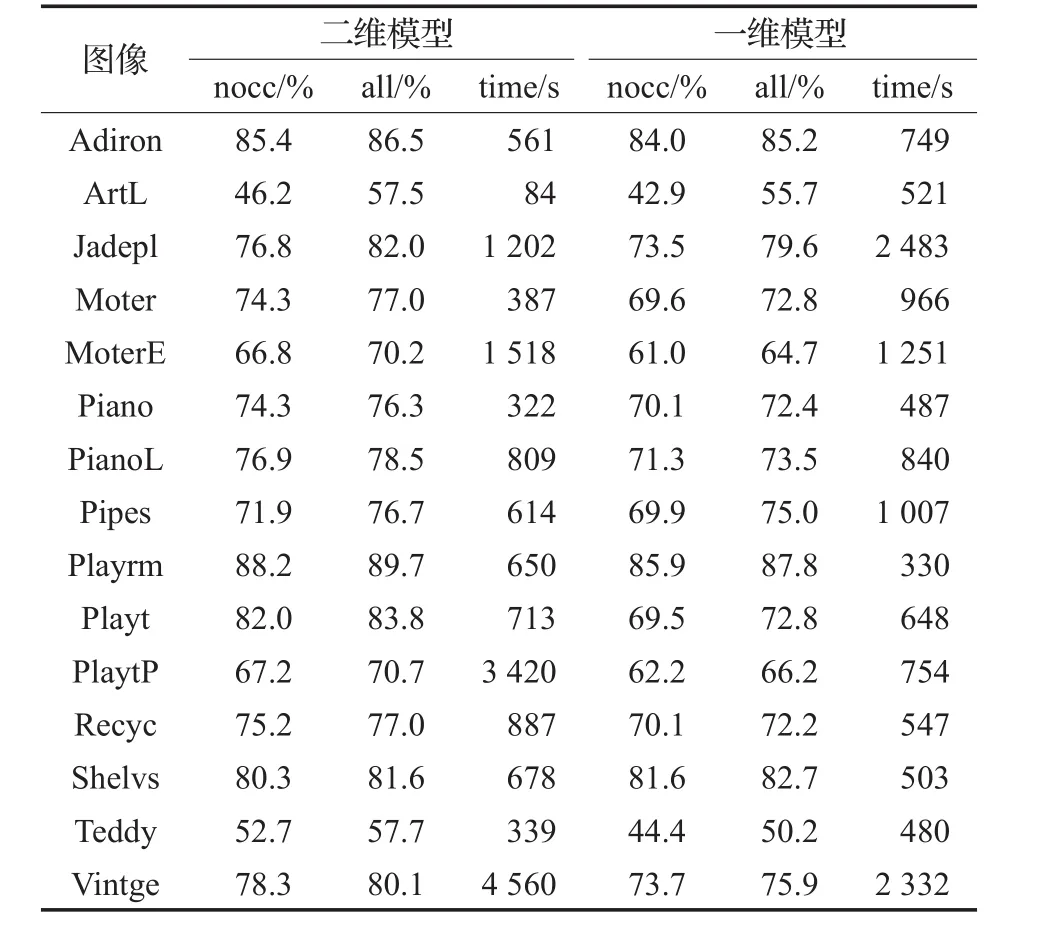
表1 图像精度及收敛速度比较

图1 部分标准库图像实验结果对比图

图2 真实场景

其中精度由错误率衡量，收敛速度由迭代时间进行度量，由数据可以得到二维模型比一维模型相比，nocc精度降低4.69%，all精度降低4.11。这是因为在二维模型中存在凸松弛，尽管是最小凸包，但是与真实最优解存在误差。关于迭代速度，一维模型、二维模型有快有慢。

图1给出部分标准库图像实验对比图，可以看到二维模型视差图像视觉效果和一维模型相当。

二维模型可以处理标准库经校准的图像，且效果与一维模型相差无几。

5.2 实拍场景图像的实验

为了验证算法的实用性，实验模拟了室内环境，用普通移动拍照设备得到4组场景图，并进行了缩放处理，得到实验所用立体图像对。然后用本文模型和一维模型得到的视差图像进行对比，如图2。

每组立体图像对均有明显的极线偏差。对本文模型与一维模型得到的视差图进行对比，可以发现本文模型可以处理极线校准不精确的图像，在细节部分更加清晰，得到的视差图像效果更好。一维模型处理真实场景图像变得很困难。

6 结束语

本文针对一维立体匹配模型极线校准不精确的问题，提出了二维立体匹配模型及其原始对偶算法。通过实验证明，二维模型可以处理标准库中图像。相比一维模型，虽然由于其中数据项的松弛，二维模型的精度平均会降低4%～5%，但是对于现实场景的图像对进行实验，二维模型可以处理真实场景图像，与一维模型相比，得到的视差图更加精确。其中松弛方法导致的标准图像库中实验精度下降问题，是下一步研究的课题。