求解无容量设施选址问题的混合蝙蝠算法

刘春苗，张惠珍

上海理工大学 管理学院，上海 200093

1 引言

无容量设施选址问题可以应用于许多不同的领域。无容量设施选址[1]问题虽然相对来说易于理解描述，但是却很难对它进行求解，它是一个NP难题。为了更好地选择相应的地址来建造一些设施，如医院、超市、学校、地铁站等，从而使得客户的需求得到最大化的满足，消耗成本最小。

目前为止，可用在求解无容量设施选址问题的算法可概括性地分成：精确型算法（分支定界法[2-3]、列生成算法、割平面算法等），近似算法（1.488-近似算法[4]），智能优化算法（蚁群算法[5]、禁忌搜索算法、遗传算法、粒子群算法[6]等）。用精确算法来求解无容量设施选址问题虽然能求得最优解，但这只能用于求解规模较小的无容量设施选址问题，并且计算速度较慢。近似算法是指在多项式时间内能够求得问题的一个解，并且其目标函数值与最优解的目标函数值之比不超过一个常数的算法[7]。智能优化算法虽适用于求解规模大的无容量设施选址问题[8]，但往往很容易陷入局部最优，一般最后求得的是满意解而不是问题的最优解。综合精确型算法的优缺点和智能优化算法的优缺点来看：一方面，改进精确算法的复杂度和应用范围，提高其运行效率。另一方面，迫切需要设计一种可以融合其他智能算法的优点，并弥补自身不足的混合智能优化算法，这不仅是求解无容量设施选址问题的研究趋势，也是求解其他任何一个NP难题的趋势。

蝙蝠算法[9]在求解全局优化问题时，具有求解速度快、效率高、通用性强、可以和其他算法很好地结合等特点，但也存在一些缺点。盛孟龙等人针对蝙蝠容易陷入局部最优和寻优精度不高的问题，通过引入一种交叉变换的方式重新更新蝙蝠种群的位置，减少了算法陷入局部极值的可能，增强了算法的寻优精度。尹进田等人使用混沌映射的方法来对算法进行初始化，增强了种群的多样性。李枝勇等人根据蝙蝠算法容易与其他算法结合的特点，将量子进化算法和蝙蝠算法相结合，提高蝙蝠的全局搜索能力。本文通过分析无容量设施选址的具体特征，改变原有的游走规则，将三种局部搜索策略、和声搜索机制与蝙蝠算法进行合理的结合，用混合蝙蝠算法求解无容量设施选址问题。本文通过求解算例，并与其他算法作比较来验证该算法的可行性和有效性。

2 无容量设施选址问题的数学模型

无容量设施选址问题一般描述为：假设待选设施的容量都没有限制，客户用I={1,2,…,n}来表示，待选设施的位置用J={1,2,…,m}来表示，cij表示设施 j到客户i之间的运输成本，fj表示设施 j的建造费用。该模型的目的是确保在每个客户的需求最大化满足的情况下确保最低的成本。

其中，I表示客户集；i表示第几个客户，∀i∈I；n表示客户总数；J表示设施集；j表示第几个设施，∀j∈J；m表示设施总数；xij=1表示设施位置 j为客户i提供服务，否则xij=0；yj=1表示在 j处建设服务设施，否则yj=0。

上述模型中，式（1）为目标函数，表示最小化运输成本与设施建造费之和；约束（2）表示每个客户必须被服务且只能被服务一次；约束（3）表示只有开放的设施才能为客户服务；约束（4）和（5）表示变量的取值范围。

记 X*是UFL问题（1）～（5）的最优解集，通过具体分析UFL问题的具体特征，得到如下定理。

定理1假设(x*,y*)∈X*为最优解集中的一个解，记对于那么存在：

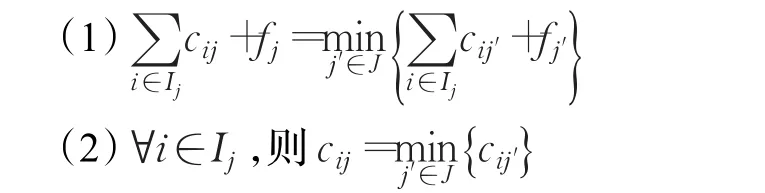
证明（1）假设存在，使下式成立：

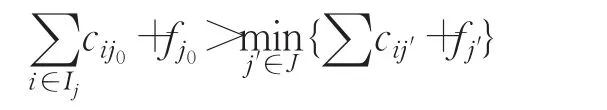
那么定义给定的无容量设施选址问题的解(x˜,y˜)为：

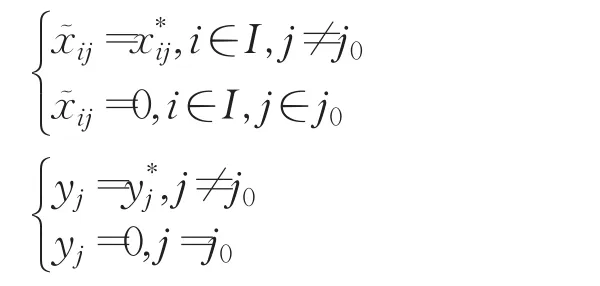
计算使得下式成立的 j″：

这与(x*,y*)∈X*是矛盾的。

（2）对于 j0∈J,假设存在i0∈Ij0,使计算使得下式成立的 j″：

并定义给定的无容量设施选址问题的解(x˜,y˜)为：

(x*,y*)是求解无容量设施选址问题的一个最优解，Ij表示设施 j为哪些客户提供服务。通过定理1可以看出，无容量设施选址问题的最优解具备两个特征：

（2）在已经开放的设施里，客户都会选择与之相对应消耗费用最少的设施为他服务。

3 基本蝙蝠算法

蝙蝠算法[10-11]是美国学者杨新社在2010年受到蝙蝠捕捉猎物的启发而提出的一种新型智能启发式算法，蝙蝠通过自己特有的回声定位方法来检测距离，采用独特的方式来区分障碍物与猎物，蝙蝠通过发射出响亮的声音脉冲，根据周围物体反射回来的回声响度和自身的双耳时间差额去建立一个三维环境的场景。蝙蝠算法[12]中寻找最优目标函数值的过程，就是将虚拟蝙蝠类比成当前的可行域内所分布的搜索点，蝙蝠通过不断飞行来寻找猎物。

3.1 虚拟蝙蝠的运动

通常需要定义虚拟蝙蝠i在d维搜索猎物的空间中它的位置xi和运行速度vi的更新方式，t时刻蝙蝠i的速度和位置的更新公式为：

其中，β∈[ ]0,1是一个服从均匀分布的随机向量；fi为蝙蝠i的频率；x*表示当前全局最优位置（解）。在实际的问题求解过程中，可以根据需要搜索范围的大小来确定 fi的值，比如令 fmin=0，fmax=100。初始时，每只蝙蝠按间的均匀分布随机赋给一个频率。

与其他仿真算法相类似的是，运行过程中出现了最优解集，从这个最优解集中选择了一个最优解，此时每只蝙蝠又随机产生了局部解[13-15]。局部搜索时，每只蝙蝠的新位置可通过式（9）产生：

3.2 音量和脉冲发生率

通常情况下，在接近猎物的过程中，响度会逐渐降低，脉冲发射的速率会逐渐提高。音量Ai和脉冲发射速率ri的更新公式如下：其中，α和γ分别表示音量衰减系数和脉冲频度增加系数，随着蝙蝠接近猎物的过程，音量是不断降低，脉冲频率是不断增加的[16]，二者均为常量。实际上，α类似于模拟退火算法中冷却进程中的冷却因素。不难发现，对于任意的0＜α＜1，γ＞0，都有：

实际应用中，通常使用α=γ=0.9。

4 求解无容量设施选址问题混合蝙蝠算法

4.1 开放设施的改进方法

局部搜索方式1（交换法）采用实数编码的方式，在已经开放的设施中，通过随机交换一部分不同客户所对应的设施来改进当前解。

例如：如图1所示，假设客户i1由设施1服务，客户i2由设施2服务，采用交换法对图1中的设施进行变换，以(i1,1)、(i2,2)替代(i1,2)、(i2,1)。

图1 交换法示意图

需要注意的是：当利用交换法变化前后的成本满足ci1,1+ci2,2＜ci1,2+ci2,1，则说明交换设施服务得到了改进。

局部搜索方式2、3以定理1为基础，本文除了运用上述局部搜索方法，还将定理1中的两大有效的局部搜索策略与蝙蝠算法结合，求解无容量设施选址问题。通过下面的例子来对定理1的这两种策略进行简要介绍：

给定一个m=5和n=5的无容量设施选址问题，矩阵C表示客户到设施之间的运输费用，F表示设施的建造费用。

上述例子的最优解是101。假设蝙蝠算法中L只蝙蝠搜索的满意解为x14=1,x23=1,x32=1,x42=1,x55=1,y1=0,y2=1,y3=1,y4=1,y5=1,即设施开放集合为{2，3，4，5}；客户1选择了设施4，客户2选择了设施3，客户3和客户4选择了设施2，客户5选择了设施5；消耗的总费用之和为19+14+12+10+122+174+122+178+114=765。

下面使用两种局部搜索方法对蝙蝠算法的求解结果进行改进：

搜索策略1本文以设施2服务客户3和客户4为例，客户3和客户4分别同时被其他各个设施服务所消耗的成本为：客户3和客户4被设施1服务的费用为284，客户3和客户4被设施2服务的费用为319，客户3和客户4被设施3服务的费用为321，客户3和客户4被设施4服务的费用为158，客户3和客户4被设施5服务的费用为159。根据计算结果以及定理1得出，如果客户3和客户4选择了为其服务成本最低的设施4，则可以使得蝙蝠算法的求解结果得到改进。那么令x32=0，x42=0,x34=1,x44=1,y2=0,y4=1。同理其他的也都可以改进，最后得出结果为x14=1,x23=1,x34=1,x44=1,x55=1,y1=0,y2=0,y3=1,y4=1,y5=1,总的成本为592。

搜索策略2 min{c13,c14,c15}=19，设施5应为客户1服务，min{c23,c24,c25}=13,设施4应为客户2服务，min{c33,c34,c35}=12，设施4应为客户3服务，min{c43,c44,c45}=11，设施5应为客户4服务，min{c53,c54,c55}=10，设施3应为客户5服务，v=101。

经过两个策略计算，蝙蝠算法的求解结果明显得到了改进。

4.2 游走法则的改进

通过分析蝙蝠算法的主要特性，发现通过式（9）的游走法则来寻找目标的搜索能力较弱，因此本文给出了一个新的游走法则，增强蝙蝠的搜索能力，公式如下：

其中，μ是惯性因子，μ=1-ω,ω=ωmax-(ωmax-ωmin)×t/MaxIter；ψ∈[-1,1]；xold是最佳蝙蝠的位置；xk是从种群中随机选取的任一只蝙蝠的位置。

4.3 和声算法

为了进一步改进蝙蝠算法的局部搜索能力，平衡蝙蝠算法的开发能力和探索能力，在蝙蝠算法中融入并改进了和声搜索机制。

2001年，Geem等人首次提出了和声搜索（Harmony Search，HS）算法，这种算法原理来自于乐队演奏，每个乐器的音符都代表着目标函数中的变量，演奏目的是使得音乐更加动听，同样算法的优化目的就是寻找到全局最优值。在HS算法中，各乐器声调的每个和声相当于一个解，并通过一个n维实向量表示。在和声搜索算法中存在一个和声记忆库，用来存放解集，和声记忆库的大小表示种群的大小，存储在和声记忆库中的和声向量和目标函数值用矩阵来表示。在和声算法中初始解是随机产生的，初始化之后，算法通过三种方式产生新的和声向量xnew，包括记忆考虑、音调调整和随机选择，公式如下：

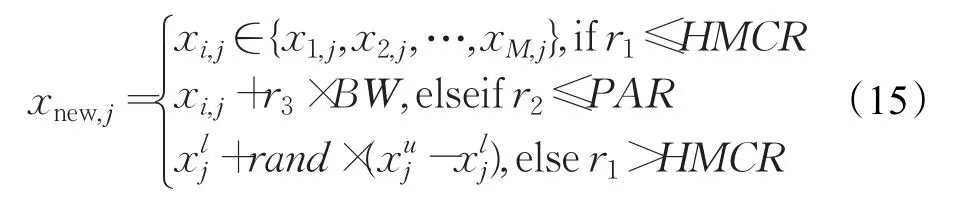
其中，r1,r2∈[0,1]是服从均匀分布的随机向量；r3是区间[-1,1]之间的随机数；HMCR∈[0,1]表示和声记忆库考虑概率，用它来决定是否从和声记忆库中选择xnew；PAR∈[0,1]表示微调概率，它用来决定变量是否进行调整；BW表示的是音调微调带宽。

一个新的和声向量xnew产生以后，和声记忆将通过比较xnew和最差和声向量xw的值来更新和声记忆库，如果xnew的值优于xw的值，那么xw将被xnew取代。

在本文算法中，采用和声搜索机制产生候选解xnew，通过与和声记忆库中最差的和声向量xw比较，来决定是否接受产生的新解。为了更好地利用当前最优解，重新更改了和声搜索机制，公式如下：

其中，τ=1-ω；r1,r2∈[0,1]是一个服从均匀分布的随机向量；r3、r4是区间[-1,1]之间的随机数；xk1,j、xk2,j、xk3,j是随机选取种群中的解；表示当前最优解中的第 j个值，j=1,2,…,n。从上式中可以看出，如果r1≤HMCR,xnew,j是由当前最优解产生的，这个过程类似于和声算法中的记忆考虑；如果r2≤PAR,xnew,j是通过扰动进行微调，这个过程类似于和声算法中的音调调整。担当的角色类似于和声算法中的BW，如果r1＞HMCR,xnew,j则通过随机选择产生，这个过程也类似于和声算法中的随机更新规则。在式（16）中，HMCR和RAR是不断变化的，更新公式如下：

其中，t是当前迭代次数；max cycle是最大迭代次数；HMCR(t)是随着t变化的和声记忆库取值概率；HMCRmax和HMCRmin表示最大保留概率和最小保留概率。

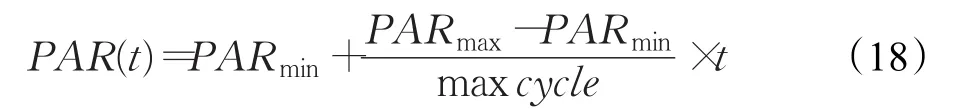
其中，PAR(t)是随着t变化的和声记忆库的微调概率；PARmax和PARmin表示最大扰动概率和最小扰动概率。从式（16）可以看出，当前最优解是从新的候选解中产生的，HMCRmax和HMCRmin是不断线性增加的。因此，蝙蝠在早期进行随机搜索，随着迭代次数的增加，主要集中在当前最优解附近搜索。

4.4 混合蝙蝠算法求解无容量设施选址问题的实现过程

步骤1设置蝙蝠的种群大小为N，最大迭代次数Max Iter，蝙蝠i的初始响度，脉冲发射率，最小脉冲频率 fmin和最大脉冲频率 fmax，脉冲音强衰减系数α和脉冲频度增加系数γ。

步骤2随机产生每只蝙蝠所对应的初始解，产生的初始解对应的是每个客户都得到一个开放的设施为他们服务，并且每个客户仅仅被一个设施服务，如一组解[2 1 3 5 3]则表示5个客户分别被设施1、2、3、5服务。

步骤3计算与每只蝙蝠所对应的目标函数值fitness(i)(i=1,2,…,N)，并记当前最优解为X*及其对应的目标函数值为gfvalue。

步骤4判断该算法是否取得了最优解或者达到了最大迭代次数MaxIter，如果取得了最优解或者达到了最大迭代次数，算法结束，此时输出它的最优解；否则，转步骤5。

步骤5根据式（6）～（8）计算得出蝙蝠i的一个待定解Xnew。通过频率和速度更新位置Xnew，不一定每个客户都能得到正确的分配，此时需要对产生的解进行处理。首先找出未能得到正确分配的客户，对他们采用运输成本最低的方式进行重新分配。用交换法对Xnew进行局部优化，直到交换出最优解，则停止使用交换法。

步骤6产生一个随机数rand1，如果rand1＞R0(i),则用式（14）得到一个新的待定解Xnew，此时运用定理1的两大局部搜索策略、和声搜索进一步提高蝙蝠的搜索能力和寻优精度。

步骤7产生一个随机数rand2，如果rand2＜A(i)且 fitness(Xnew)＜gfvalue，则转入步骤8。

步骤8接受这个蝙蝠飞行产生的新解，并根据式（10）和（11）更新响度A(i)和脉冲发射率R0(i)。

步骤9排列蝙蝠的位置并找到最佳位置X*，并返回到步骤4。

混合蝙蝠算法流程如图2所示。

5 算例分析

为了验证混合蝙蝠算法在求解无容量设施选址问题上的可行性、有效性和优越性，本文采用了UFL基准问题库中的12个算例数据对目标函数进行求解，并对基本蝙蝠算法、基本蚁群算法、混合蚁群算法和混合蝙蝠算法求解无容量设施选址的计算结果进行了对比分析。利用MATLAB（R2008b）编写程序，算法的实验环境为Intel®CoreTMi7-6500U CPU@2.50 GHz，4 GB内存的Windows 7操作系统。

参数的选取可以根据具体的实际情况进行调整，本文测试算法时的参数取值包括：蝙蝠的个数N为20；音量衰减系数用α表示，取值为0.9；脉冲频度增加系数用γ表示，取值为0.9；最大惯性权重用ωmax表示，取值为0.9；最小惯性权重用ωmin表示，取值为0.9；最大迭代次数 MaxIter为200次；和声算法中的最大保留概率HMCRmax为0.99，最小保留概率 HMCRmin为0.9，最大扰动概率PARmax为0.5，最小扰动概率PARmin为0.1。如表1所示。

表2将基本蝙蝠算法、混合蝙蝠算法与文献[5]中的基本蚁群算法、混合蚁群算法的求解结果进行了对比，包括迭代200次的总时间和目标函数值。图3、图4和图5分别是选择三种规模算例例1（gs00250a1）、例2（gs00500a1）、例3（gs00750a1）用基本蝙蝠算法和混合蝙蝠算法求解的结果对比图。

表1 参数取值

表2 计算结果

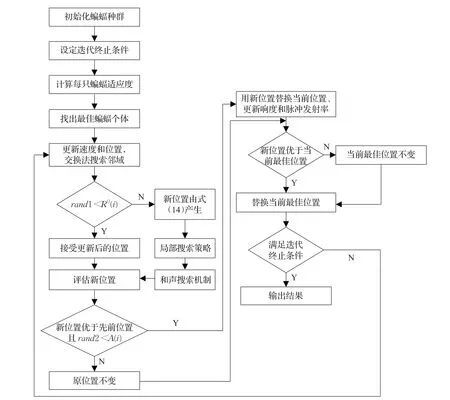
图2 混合蝙蝠算法流程图

图3 BA与Hybrid BA用例1时目标函数的收敛曲线

图4 BA与Hybrid BA用例2时目标函数的收敛曲线

图5 BA与Hybrid BA用例3时目标函数的收敛曲线

通过表2和收敛曲线图得出如下结果：基本蚁群算法、混合蚁群算法、基本蝙蝠算法和混合蝙蝠算法求解12个算例的平均运行总时间分别是651.08、671.63、5.28和81.13。混合蝙蝠算法求解12个算例的平均目标函数值为530 897，无论从时间上或者求解结果上来说都比基本蝙蝠算法、基本蚁群算法和混合蚁群算法的结果要好。加入局部搜索策略、更改种群游走规则的混合蝙蝠算法运行总时间仍然明显小于基本蚁群算法和混合蚁群算法，其结果也明显优于基本蝙蝠算法、基本蚁群算法和混合蚁群算法。在求解大规模选址算例时，蝙蝠算法计算出的结果与蚁群算法求出的结果随着规模的逐步变大，差值也越来越大，从而表明蝙蝠算法的研究价值不容小觑。总之，相对于其他三种算法而言，用混合蝙蝠算法求解大规模问题的可行性更高，收敛性能更好。

6 结束语

本文将蝙蝠算法用于求解无容量设施选址问题，根据UFL问题的具体特性，加入了三种局部搜索方法、和声搜索机制改进算法，并更新了种群随机游走规则，设计出了求解UFL问题的混合蝙蝠算法。改进后的算法极大程度地改善了蝙蝠易陷入局部最优，寻优精度不高，后期收敛速度慢的缺点。本文的求解算例结果显示出了混合蝙蝠算法在求解UFL问题上的可行性、有效性和优越性。主要创新如下：

（1）交换法的加入使得蝙蝠每次搜索解的时候，能够遍历整个邻域空间，每次得出的新解都能得到最大化的改进。

（2）重新定义的游走规则提高了蝙蝠寻找猎物的能力，在求解无容量设施选址问题时，最优解的精度得到明显的改进。

（3）根据无容量设施选址模型设计的两大局部搜索策略，不仅符合求解模型的特点，还能很好地与蝙蝠算法结合，有效避免了蝙蝠过早陷入局部最优，使得设施的分配更加合理。

（4）和声算法增强了蝙蝠的全局搜索能力，平衡了算法的开发能力和探索能力，提高了蝙蝠的收敛速度。

通过分析本次测试算例的整个过程，可以知道蝙蝠算法参数少，比其他算法易于实现，其运行时间大大小于其他算法的运行时间，同时也适应了现在快节奏生活的要求。蝙蝠算法求解的选址问题规模越大，其优点越发突显，在未来解决复杂性、大规模选址问题上用途十分广泛。为了扩展蝙蝠算法的应用领域，并进一步研究蝙蝠算法求解相关问题的可行性和优越性，利用混合蝙蝠算法求各类选址问题将是下一步的研究工作。