基于9维量子系统上的秘密共享方案

郝 娜，李志慧，白海艳

陕西师范大学 数学与信息科学学院，西安 710119

1 引言

秘密共享是密码学中的一个重要研究内容，它是指在参与者中共享秘密份额，只有授权集才能重构秘密，非授权集得不到秘密的任何消息。在一个量子秘密共享方案中，秘密是基于量子特性被分发和重构的，相对于经典秘密共享方案，量子秘密共享方案因其量子理论基础而更加安全。目前，量子秘密共享的研究主要集中在利用量子方法在通信者之间共享经典密钥的(N,N)方案。自从1998年Hillery等人参照经典秘密共享体制提出量子秘密共享的概念，并利用Green-Horne-Zeilinger（GHZ）三重态的量子关联性设计了一个量子秘密共享方案[1]之后，量子秘密共享引起了人们的兴趣，一系列量子秘密共享方案被提出[2-8]。

无偏基是许多量子信息处理过程中的重要工具。关于无偏基已有许多研究[9-14]。已有文献证明素数幂维复空间Cd上无偏基的最大数目为d+1[9]。Tavakoli等人在文献[14]中利用奇素数维量子系统上的无偏基的循环性质以及酉矩阵有关理论，给出了一个量子秘密共享方案。文献[9]借助素有限域理论将奇素数维量子系统上的无偏基用素有限域中的元素表示。当量子系统维数d为偶数时，该系统上的无偏基可以利用奇素数维上无偏基的情况类似讨论，这样当d≤8时，d维量子系统上的无偏基均已构造。本文给出9维量子系统上的无偏基以及酉矩阵，基于这些无偏基和酉矩阵的性质，构造9维量子系统上的秘密共享方案，并讨论方案的安全性。

2 无偏基及相关性质

其中，i,j=1,2,…,d，称这两组基B0和B1是相互无偏的；两两相互无偏的一组标准正交基{B0,B1,…,Bm}称作相互无偏基集。

Wootters等人指出所有素数和素数幂维系统(d=pn,p≠2)的无偏基的个数为d+1个，并利用有限域的理论给出了这d+1个无偏基的具体形式[9]。设 p是一个奇素数，在有限域Fpn（n是自然数）上，令：

当 j∈Fpn时，由式（2）给出的基组为：

…

当 j=m,m∈Fpn时

…

当 j=d时，令：

称由式（3）定义的这组基为计算基，对应的基记为Vd=

由于F9为F3的二次扩域，令 f(x)=x2+x+2为F3上二次不可约多项式，令θ为 f(x)的一个根，则有：

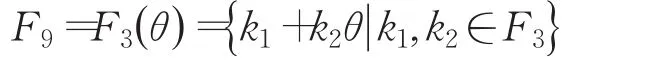
设g:F9→Z9是有限域F9到剩余类环Z9的一个映射，定义：易证g为一一映射，即F9中的元素与Z9中的元素一一对应。

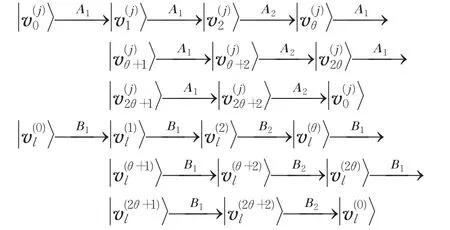
引理在有限域F9上，由式（2）定义的无偏基的上标和下标有以下性质：

例1 当l=θ+2,j∈F9时

进一步，在有限域F9上，令S={A1,A2,B1,B2}，其中：

定理1在有限域F9上，由式（2）定义的无偏基有以下性质：

（1）当l∈{0 ,1,θ,θ+1,2θ,2θ+1} 时，

（3）当j∈{0 ,1,θ,θ+1,2θ,2θ+1} 时，

证明当l∈{0,1,θ,θ+1,2θ,2θ+1}时：

因此，当l∈{0 ,1,θ,θ+1,2θ,2θ+1} 时，同理可得：

注1由定理1可得：

3 酉矩阵的构造

本文构造有限域F9上的酉矩阵，使其在集合M上是封闭的。

定理2 设对于 ∀α,β∈F9：

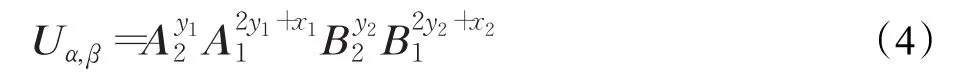
α,β

证明由于Ai,Bi,i=1,2，均为酉矩阵，易证Uα,β为酉矩阵。

设 l=k1+k2θ,j=k3+k4θ α =x1+y1θ, β =x2+y2θ

则l+α=(k1+x1)+(k2+y1)θ j+β=(k3+x2)+(k4+y2)θ

由定理1，得：

所以：

4 (N,N)门限方案

文献[14]给出了奇素数维上的秘密共享方案，本节考虑9维量子系统上的情形。设R1为分发者，R2,R3,…,RN+1为参与者。

4.1 准备阶段

4.2 分发阶段

（1）R1随机选定相互独立的 α1,β1∈F9，则 α1=其中，那么，用作用，将作用后的量子态记为，并将传给R2。

（2）R2随机选定相互独立的 α2,β2∈F9，则 α2=，其中，那么，用 U作用，将α2,β2作用后的量子态记为，并将传给R3。

（3）R3随机选定相互独立的 α3,β3∈F9，则 α3=，其中，那么，用作用，将作用后的量子态记为，并将传给R4。

（4）重复此过程直到 RN+1得到量子态RN+1将传给R1。

4.3 测量阶段

R1随机选择J∈F9，用基测量量子态，若测量结果为，标记h,h∈F9。

4.4 检测阶段

在随机的轮中，参与者Rk,k=2,3,…,N+1公布他们选择的βk,R1不公布任何数据，R1私下计算下式是否成立：

若上式成立，则该轮有效，否则，放弃该轮。

为了检查安全性，只需让参与者 Rk,k=2,3,…,N+1公开他们选择的αk,R1计算下式是否成立：

若成立，则安全；否则，该轮就是不安全的，存在窃听或欺骗。

4.5 恢复阶段

Rk,k=2,3,…,N+1共享他们的αk，得到密钥：

注2该方案之所以可以运行，是因为：

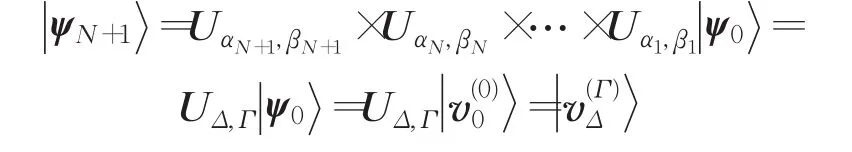
分析：当选择的 J∈F9不满足式（5）测量量子态时就会塌缩为别的量子态，后边的计算就没有意义了，也即该轮为无效轮；当选择的J∈F9满足式（5）时就可以准确测量，又F9含有9个元素，因此准确测量的概率为1/9，即该轮有效的概率为1/9；若该轮测量有效，假设不存在欺骗或窃听，则准确测量之后，式（6）一定满足，因此式（6）可以用来判断安全性；每执行一轮有效安全的上述协议，就会产生一个密钥，当多次执行上述协议就会得到密钥流s1,s2,…,可用于秘密共享。因此，可以由式（5）和式（6）判别该方案的有效性和安全性。

5 安全性分析

本文从以下两方面来讨论该方案的安全性。

5.1 外部攻击

类似Bennett-Brassard协议（简称BB84协议）中两方量子密钥分发（Quantum Key Distribution，QKD）情形的攻击：对于更多一般的窃听攻击，在Rk→Rk+1的量子传输中，可以将R1,R2,…,Rk视为一块，有效地表示为单一团体，把Rk+1,…,RN+1,R1视为测量团体，因此窃听攻击就被简化为之前遇到的BB84中两方QKD的情形，可以类似地探讨，很显然是安全的。

通过酉门的攻击：还有一种可以选择的欺骗是Eve给参与者Rk的酉门再发送一个量子底特或一个多体量子底特脉冲，以便于她可以以某种方法通过酉门达到窃听，而不是截获协议中的量子态。当βk被公开之后，她就可以知道真正的酉阵，就可知道αk。然而，如果Rk确定了他的酉门的出口处量子测量的次数，这种攻击是很容易被检测的。

纠缠测量攻击：在传输量子态的过程中，假定Eve使用酉算子UE纠缠辅助粒子，并通过测量辅助粒子以窃取秘密信息。假设Eve的辅助粒子是，且有如下形式：l∈F9)是通过酉算子UE决定的纯态，且

为了避免窃听检测，Eve必须设置akl=0，其中k≠l且k,l∈F9。因此方程（7）和方程（8）可简化为：

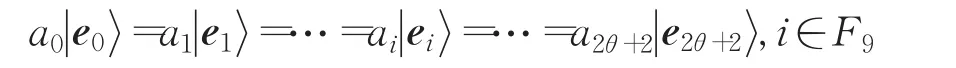
在方程（11）中，容易看出，如果Eve想要避免窃听检测，那么她并不能对整个量子秘密共享系统产生影响，并且从辅助粒子中也得不到有效信息。因此，纠缠测量攻击是无效的。

特洛伊木马攻击：若量子秘密共享（Quantum Secret Sharing，QSS）方案中使用的粒子是光子，则所提出的协议对于以下两种特洛伊木马攻击可能是不安全的：延时光子攻击和不可见光子攻击。为了阻止延时光子攻击，参与者必须有能力区分是否存在多光子信号，即必须能够区分所接收到的光子是单光子和多光子。光子数分裂（Photon Number Splitting，PNS）技术可以实现这一要求。参与者将随机选择收到的光子信号的一部分作为样本信号，并用PNS技术来区分每个样子信号。随后，他们任意选择一般基测量两个信号。如果多光子率太高，传送过程应该停止并重新开始。为了阻止不可见光子攻击，参与者需在设备上增加滤镜。而滤镜只允许光子信号的波长接近于操作粒子的波长的光子进入。故攻击者的不可见光子将会被隔离。

5.2 内部攻击

在秘密共享中，须承认参与者子集密谋欺骗的可能性。在最坏的情形下，只有分发者R1和一个参与者是诚实的，剩下的N-1个参与者是密谋方。这里针对一些特殊的阴谋攻击进行分析。

在文献[15-16]中，窃听攻击使用量子记忆和辅助量子态纠缠测量系统，这种攻击在文献[17]中被证明会导致安全性问题。然而，文献[16]中的攻击不仅需要第一个参与者进行欺骗，还需要最后一个参与者也是骗子。这在本文中永远不会发生，因为R1是第一个也是最后一个参与者是诚实的。而且，文献[16]中的窃听攻击需要知道β1和J，这是不可能的，因为R1从未公开任何数据。

更一般的，骗子可以使用一些基于纠缠一个辅助量子态或在量子记忆中储存协议量子比特或产生一个新的纠缠态的攻击，在协议循环中，一个子系统可以进一步通信。不过他们不能获利，原因是缺乏分发者R1公布数据，导致骗子有效可用的量子比特都在混合状态，而没有给出一个可能结果的可观测量。而且，如果骗子联合他们在诚实参与者上做的窃听攻击，根据上一节的论证，他们将在协议的检测阶段被检测到。

为方便理解上述方案，举例如下。

例2假设N=3，考虑一个(3,3)方案。

（1）准备阶段

分发者R1准备量子态：

（2）分发阶段

① R1随机选定 α1,β1∈F9，令 α1=1+θ,β1=θ 。因此，x11=1,y11=1,x12=0,y12=1。

② R2随机选定 α2,β2∈F9,令 α2=θ,β2=1。因此，x21=0,y21=1,x22=1,y22=0。

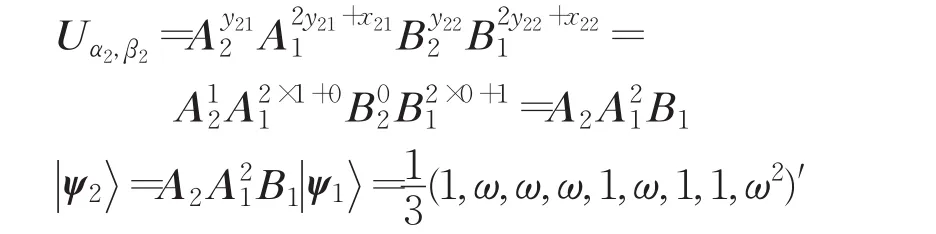
③ R3随机选定 α3,β3∈F9,令 α3=θ,β3=θ。因此，x31=0,y31=1,x32=0,y32=1。

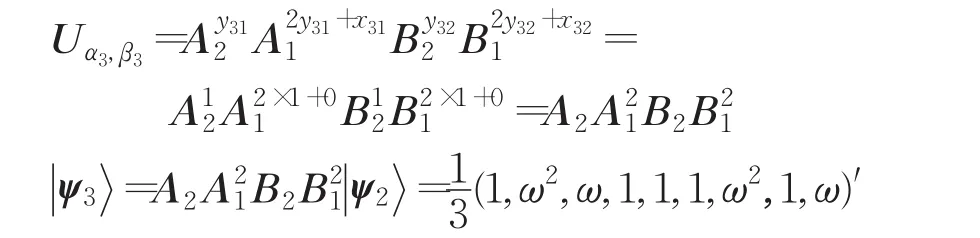
④ R4随机选定 α4,β4∈F9,令 α4=θ+2,β4=θ+1。因此，x41=2,y41=1,x42=1,y42=1。

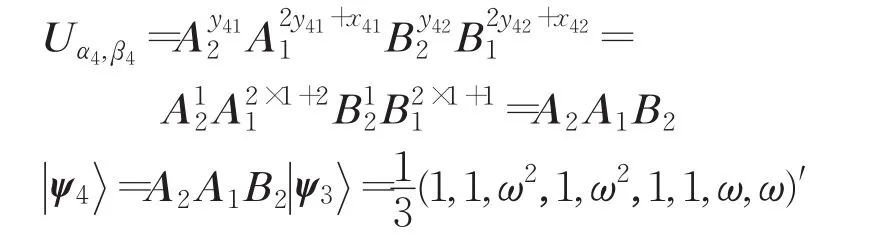
（3）测量阶段

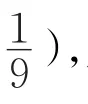
（4）检测阶段

R2、R3、R4公布他们的 β2、β3、β4，R1检查式（5）是否成立：

因此本轮有效。之后R1检查式（6）是否成立：

因此本轮安全。

（5）恢复阶段

Rk,k=2,3,4共享他们的αk，得到密钥：

因此本轮生成的密钥为s=2。

6 结束语

本文首先介绍了文献[9]基于有限域理论在奇素数幂维系统上无偏基的构造方法；其次针对具体的非素有限域F9给出了关于这些无偏基的性质，并基于这些性质构造了酉矩阵，进而提出了一个量子秘密共享方案。本文方案构造了一个只涉及一个qudit的单粒子量子协议，虽然该协议没有考虑可能的复杂攻击，但能抵御标准的攻击。它相比别的方案在可扩展性上展现了很大的优点，对于任意多个参与者N，都可以利用该方法实现一个9维量子系统上的(N,N)门限方案。另一方面，相比文献[14]，将素有限域维量子系统推广到了非素有限域F9上，对文献[14]进行了完善。在未来的工作中会继续深入研究非素有限域上的量子秘密共享方案，以便就量子秘密共享协议的设计提出更加系统的理论基础。