区间Pythagorean模糊交互式多准则决策模型
2018-11-17高雷阜
李 娜,高雷阜,王 磊
1.辽宁工程技术大学 基础教学部,辽宁 葫芦岛 125105
2.辽宁工程技术大学 理学院,辽宁 阜新 123000
1 引言
多准则决策主要研究在多个准则下选择最优方案或对有限的方案进行排序和评价,是决策分析理论的重要内容之一,其理论与方法在经济、管理、工程和军事等诸多领域都有广泛的应用[1-4]。由于客观事物的复杂性和不确定性,现代大型决策往往不仅需要多个决策者参与,而且需要多次反复、不断地对决策意见进行协调和修正,因此,交互式决策过程显得十分重要。徐泽水[5]充分利用已知客观信息的同时又可最大限度地考虑决策者的交互要求下,提出一种交互式多准则决策方法,从而使决策更具合理性。徐泽水[6]提出了一种基于残缺互补判断矩阵的交互式群决策方法。陈建中等[7]基于TOPSIS的方法,提出一套可以综合序数性偏好表示,多轮交互逐步逼近的群决策综合方法。王玉宝[8]提出一种基于方案集缩减策略的交互式多属性决策方法。周宏安[9]提出了基于方案贴近度和满意度的交互式多属性决策方法。
由于客观事物的复杂性、不确定性以及人类思维的模糊性,当决策者受一些主、客观因素制约时,他们往往以不确定语言方式描述评价信息。Xu等[10]研究了准则权重信息部分已知,评价信息由三角模糊数刻画的交互式决策问题。文献[11]基于概率权重具有稳定性和结果价值具有模糊性两项条件,提出了两层交互式有限理性决策方法。在部分权重信息下的不确定语言环境下,文献[12]建立了一些决策者与分析者之间不断交互的线性规划模型,然后在此基础上提出了一种实用的交互式选择最佳方案的方法。在直觉模糊环境下,肖建彪[13]在部分权重信息下,基于方案的期望水平、达成度、满意度等概念,提出了一种交互式多属性决策方法。Xu[14]将文献[10]的模糊环境下的研究结果推广到直觉模糊环境下。胡浩等[15]通过计算各个专家对方案的偏好矢量与理想方案偏好矢量间的相似度,提出了直觉模糊动态信息下的交互式决策方法。
在实际决策过程中,由于环境的复杂性和人的认知,决策者可能给出一个方案满足和不满足一个准则的程度之和大于1的情况。例如:评价软件开发项目,对于技术可行性这个准则,决策者给出具有这个准则的程度为0.5,而不具有这个准则的程度可能为0.6,由于0.5+0.6>1,直觉模糊数无法描述,但0.52+0.62=0.61<1。为此,Yager等[16-17]于2014年提出了Pythagorean模糊集,其特点是隶属度与非隶属度之和可以大于1,但隶属度与非隶属度的平方和小于等于1,可见Pythagorean模糊集是对直觉模糊集的一种扩展,因此在处理模糊性和不确定性信息方面具有更强的表现能力。目前在Pythagorean模糊环境下,多准则决策已有一些研究[18-21],但交互式多准则决策问题还未见报道。为此,本文在准则权重信息部分已知的情况下,研究准则值为区间Pythagorean模糊数的交互式多准则决策问题。
2 基本概念
定义1[16]设X为一个给定论域,称P={<x,μP(x),vP(x)>|x∈X}为 X上的Pythagorean模糊集,其中,μP(x)∈[0,1],vP(x)∈[0,1],且表示x对p的隶属程度,vP(x)表示x对 p的非隶属程度,为x对 p的犹豫度。
为了表示方便,称 α=(μα,vα)为 Pythagorean 模糊数[14],其中,记X上的Pythagorean模糊数为PFN(X)。
定义2[16]设 X 为一个给定论域,称为 X 上的区间Pythagorean模糊集,其中且,犹豫度区间为:

定义3[17]令,称为区间Pythagorean模糊数˜的得分值,其中s为得分函数。显然越大,越大。
3 区间Pythagorean模糊信息下的交互式多准则决策
3.1 问题描述

定义4 设为第 i个方案,ω =(ω1,ω2,…,ωn)T为准则权向量,称
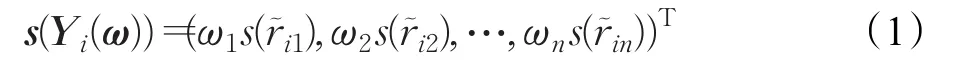
为方案Yi的加权得分向量,且称

为 s(Yi(ω))的模。
方案Yi,i=1,2,…,m的模s(Yi(ω))越大,表明方案Yi,i=1,2,…,m 越好,若准则权向量 ω=(ω1,ω2,…,ωn)T已知,则通过式(2)得到每个方案的模,进而通过模的大小进行排序。实际决策过程中,往往对准则权向量信息的了解只是部分的,接下来研究准则权重不完全确定情形下的决策。
3.2 准则权重的确定
定义5分别称

为区间Pythagorean模糊正理想方案和区间Pythagorean模糊负理想方案,其中:
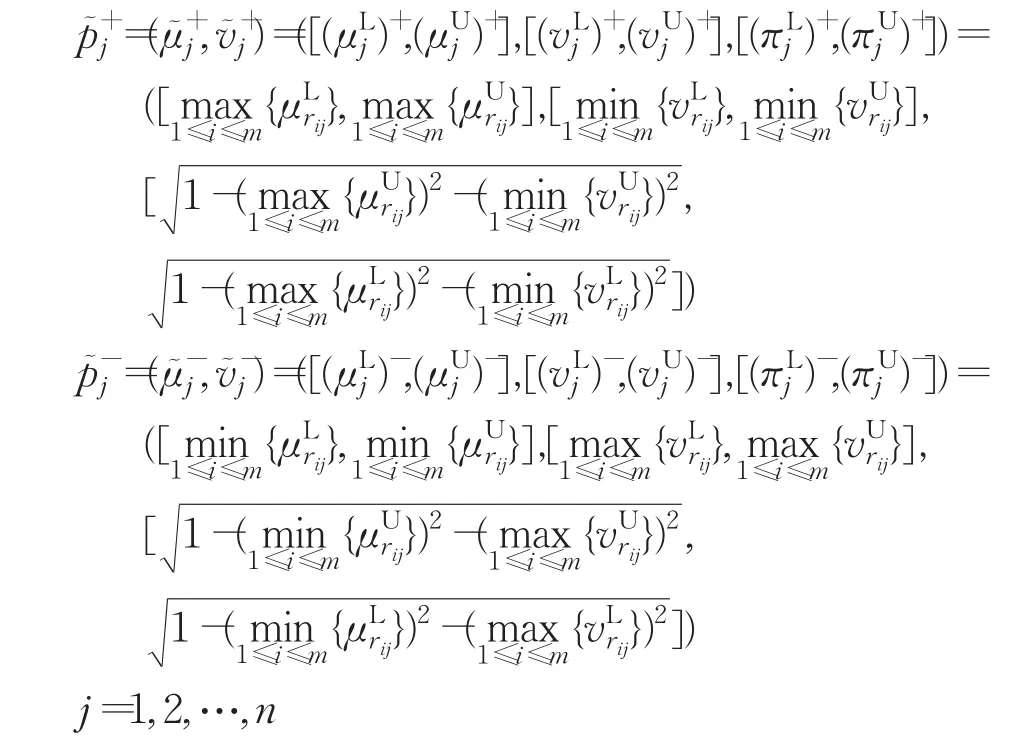
定义6 设为区间 Pythagorean 模糊正理想方案为准则权向量,称
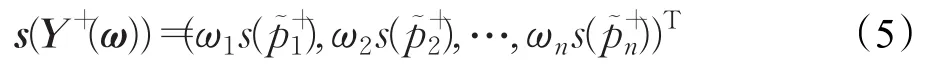
为区间Pythagorean模糊正理想方案Y+的加权得分向量,且称

为 s(Y+(ω))的模。
类似定义6有定义7。
定义7 设为区间 Pythagorean 模糊负理想方案,为准则权向量,称

为区间Pythagorean模糊负理想方案Y-的加权得分向量,且称

为 s(Y-(ω))的模。
定义8设

分别为方案Yi和区间Pythagorean模糊正理想方案Y+的加权得分向量,称

为s(Yi(ω))和s(Y+(ω))的相关系数,即夹角余弦。并称

为 s(Yi(ω))在 s(Y+(ω))的投影。的值越大,说明 s(Yi(ω))越接近 s(Y+(ω)),即方案Yi越好。关于相关系数显然有如下结论。
定理1设

分别为方案Yi和区间Pythagorean模糊正理想方案Y+的加权得分向量,则:

类似定义8,有定义9。
定义9设

分别为方案Yi和区间Pythagorean模糊负理想方案Y-的加权得分向量,称
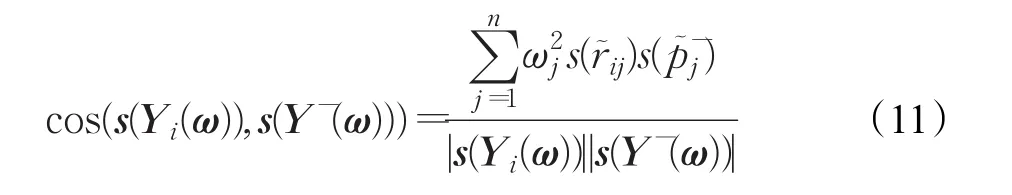
为s(Yi(ω))和s(Y-(ω))的相关系数,即夹角余弦。并称

为 s(Yi(ω))在 s(Y-(ω))的投影。
定理2设
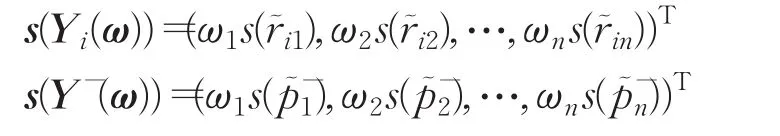
分别为方案Yi和区间Pythagorean模糊负理想方案Y-的加权得分向量,则:

决策过程中,仅仅单独利用式(10)或(12)评价方案并不全面,为此将式(10)和(12)综合起来,得到定义10。
定义10称

为方案Yi的满意度。
满意度μ(Yi(ω))反映了方案Yi总属性值的大小,μ(Yi(ω))的值越大,说明方案 Yi越好,且 μ(Yi(ω))∈[0,1]。
为了确定权重,建立如下多目标优化模型:

其中,H为属性权重信息不完全的数学表达式集合。
根据多目标优化理论中的线性加权和法,考虑到各个方案之间的公平竞争,模型(14)可转化为如下的单目标优化模型:

定理3单目标优化模型(15)的最优解为多目标优化模型(14)的有效解。
证明方法同文献[13]。
3.3 交互式决策步骤
考虑到决策者的偏好,实际决策过程中由模型(14)和模型(15)解出的某些方案的满意度过大,相比而言另一些方案的满意度过小,决策者可能要对方案的满意度进行调整,为此建立如下交互式优化模型:
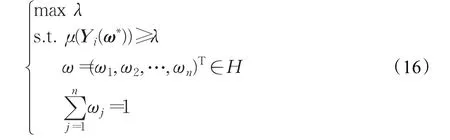

定理4单目标优化模型(17)的最优解是多目标优化模型(14)的有效解。
证明方法同文献[13]。
基于以上分析,下面给出Pythagorean模糊信息下权重信息不完全确定的区间多准则决策问题的交互式决策方法。
步骤1利用模型(16)求出初始最优权重向量ω(0)=计算每个方案的初始满意度i=1,2,…,m,决策者据此给出每个方案满意度的下限值λ(0)i,i=1,2,…,m。令c=1。
步骤2利用模型(17)求出最优权重向量计算每个方案的满意度2,…,m。
步骤3若决策者对步骤2的所得结果满意,则利用式(2)计算出的每个方案的模 s(Yi(ω)),i=1,2,…,m,对方案进行排序,并转步骤4。若模型(17)无解或者决策者对结果不满意,则决策者根据需要适当提高一些方案的最低满意度,同时降低另一些方案的最低满意度,令c=c+1,然后转步骤2。
步骤4结束。
4 算例分析

步骤1利用模型(16)建立优化模型(18)。
步骤2利用模型(17)建立优化模型(19)。
利用软件Matlab7.0求解该模型,无解。表明决策者给出某些方案满意度的下限值相比初始权向量确定出的满意度过大,如方案
下面决策者对方案满意度的下限值进行调整,如下:

表1 区间Pythagorean模糊决策矩阵R


表2 两种方法结果对比
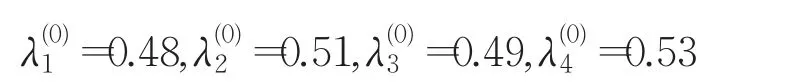
于是重新求解模型(19)得最优准则权重向量为:

由该准则权向量计算每个方案的满意度为:

步骤3决策者对此结果感到满意,利用式(2)算得每个方案的模为:


于是得到排序结果为:
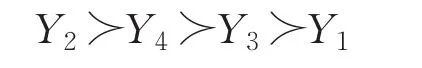
表明高新技术企业Y2在风险评估方面评价结果最好。
为了验证本文方法的有效性,计算得权重ω=(0.15,0.20,0.20,0.30,0.05,0.10),利用文献[22]中的区间Pythagorean模糊加权平均(IVPF-WAA)算子,对各个方案的信息进行集结,并通过各个方案的得分获得排序结果,与本文方法比较如表2所示。
由表2,两种方法得到的排序结果完全一致,表明了本文方法的有效性。但本文的决策方法体现了反复、不断地对决策意见进行协调和修正的一种动态过程,优于IVPF-WAA集结算子。虽然文献[13]提出了一种交互式决策方法,但该方法只适用于评价值由直觉模糊数刻画,即要求隶属度与非隶属度之和小于等于1,而对于本文中的评价值由区间Pythagorean模糊数刻画的决策问题,文献[13]的方法无法解决。由此表明,本文方法具有一定的优越性,更适合于复杂环境下的决策。
5 结束语
交互式决策是多准则决策的一个重要研究内容,在实际决策过程中,由于环境的复杂性和人的认知评价信息往往带有不确定性,本文在准则权重信息部分已知情况下,利用区间Pythagorean模糊数的得分函数确定每个方案的加权得分向量、区间Pythagorean模糊正理想方案的加权得分向量以及区间Pythagorean模糊负理想方案的加权得分向量,进而给出方案满意度的概念,并且建立关于准则权重的最优化模型,通过模型求解得到最优准则权向量。考虑到决策者对方案满意度的主观要求,依据方案满意度和决策者给出的满意度的下限值建立了交互式决策优化模型,通过对方案满意度的给定和修正来实现人机交互决策,使决策方案满足决策者的要求,并使各方案尽可能达到最优状态,丰富了Pythagorean模糊多准则决策的研究内容。本文的决策是在属性权重数学表达式集合已知的情形下进行的,后续的研究将结合实际问题背景进一步分析确定权重约束。
