基于学生思维发展的解题教学
2018-11-17江苏省如东高级中学杨晓华
☉江苏省如东高级中学 杨晓华
单纯讲解参考答案的解题教学是无法展露学生思考的过程与问题的,因此,教师在具体的解题教学中应引导学生展开自主探究与合作交流并促使其解题思维得以完全展露,这对于培养学生分析问题、解决问题的能力来说是极其有效的.
某次数学活动中,某教师执教的一道解析几何与向量的综合题至今令笔者记忆犹新.本文结合该执教教师的具体教学以及自己的思考浅谈一点想法.
问题1:已知点P(1,3)与⊙O:x2+y2=3,过点P作动直线l和⊙O相交于A,B两点,在线段AB上取一点Q,满足:(λ≠0,λ≠±1).求证:点Q始终在某一定直线上运动,请尝试求出该定直线的方程.学生在一定的思考后进行了一定的演算.师:大家以为解决此题应先设什么呢?(学生无应答)
师:题目中给出了一些向量的条件,因此我们可以先设各点的坐标.
师(板书):方法1:设A(x1,y1),B(x2,y2),Q(x0,y0).
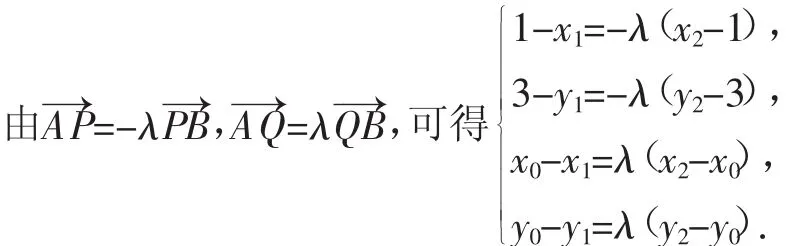
“不会吧?”“参数这么多要怎么办?”“怎么会这么设呢?”种种疑问在学生窃窃私语中显露出来,从学生的疑问来看,学生更多的思考集中在“为什么这么设”这一问题上,对于接下来应该如何解决此题并没有多作思考.
师:然后对等式进行整理.
(学生未作反应)
师(板书):即

此时,有少部分学生的思维与教师的解题产生了共鸣.
生1:根据①③两式可得出x1,x2,根据②④两式可得出y1,y2,将所得结果代入所在圆的方程即可消去参数x1,x2和y1,y2,点Q所在的直线方程应该也就好解了.
师(板书):很好.
①×③,得x12-λ2x22=x0(1-λ2),⑤
②×④,得y12-λ2y22=3y0(1-λ2).⑥
因为点A(x1,y1)、B(x2,y2)在圆x2+y2=3上,
⑤+⑥,得3-3λ2=(x0+3y0)(1-λ2).
又因为λ≠±1,因此x0+3y0=3.
故点Q始终在定直线x+3y=3上运动.
听课老师听课至此均发出了赞许声,执教教师将题中向量与设点间的关系进行了小结便进入了下一题的例题讲解.笔者以为,听课教师所表达的赞许应该是对学生给出的.事实上,执教教师对这一例题的讲解仍然有可以完善补充的.学生在教师讲解此题的过程中并没有表现出对这一解法较高的接受程度,在学生身上表现得更为明显的是学生对解题方法如此精巧的感叹,学生对此题解题思路的由来并没有作出更多的感知与思考.事实上,遵循学生的思路可以得出以下方法.
两式相减,得2(2x0+6y0)(1-λ)2=12-12λ2.
又因为λ≠±1,因此x0+3y0=3.
故点Q始终在定直线x+3y=3上运动.
平方相加再进行整理虽然看上去比较复杂,但整理方向却会因为式子的结构特点而变得更加明确,看似繁杂的过程却没有太大的难度.事实上,在解题时,我们不难发现,直线l绕着点P旋转才是造成点Q如此运动的根源,因此,问题归结为直线l的斜率并可得出以下解法.
方法3:当直线l的斜率存在时,设其斜率为k,设A(x1,y1),B(x2,y2),Q(x0,y0).则l:y=k(x-1)+3,把直线方程代入圆方程并整理可得(1+k2)x2+2k(3-k)x+(3-k)2-

综上,点Q始终在定直线x+3y=3上运动.
这一例题是笔者在课堂上跟学生讨论过的,学生首先提出的方法就是引入斜率进行解题.方法3与方法1相比虽然运算量较大,但学生能抓住直线的斜率这一本源,同时,学生受方法1的影响还想到了从其他角度来运用坐标间关系的方法,这就是此题的第4种解法.
故λx2=x1+λ-1,λy2=y1+3(λ-1).
又因为A,B两点均在圆x2+y2=3上,所以x12+y12=3,且=(x1+λ-1)2+(y1+3λ-3)2=3λ2,即2x1+6y1=3(λ+1)-10(λ-1).
故(1+λ)x0=x1+λx2=2x1+λ-1,(1+λ)y0=y1+λy2=2y1+3λ-3.
所以(1+λ)x0+3(1+λ)y0=3(1+λ),
故点Q始终在定直线x+3y=3上运动.
执教教师在此题的教学中是基于例题已有答案对学生进行引导与启发的,学生已有的认知结构与题目的内在规律并没有受到执教教师的重视,执教教师首先设了点的坐标并根据答案对式子进行了加工,但学生对教师此举的意图却未能领会,在教师要求学生观察式子左边的结构特点之后学生才获得了教师想要的答案.这是完全按照答案所进行的解题教学,学生的思维在这一过程中并未得到暴露,他们在教师的解题思路下进行了顺从性地参与,看似得到了完美的答案,但实际上,学生思维的发展却是远远不够的.因此,局限于教材参考答案的教法是狭隘的,教师在具体教学中不仅要引导学生进行多角度的思考,还应引导学生在椭圆的题型中拓展思维.
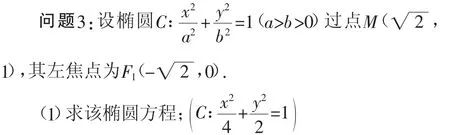
(2)当过点P(4,1)的动直线l与椭圆C相交于A,B两点时,在线段AB上取一点Q,满足|A—→P|·|Q—→B|=|A—→Q|·|P—→B|,证明:点Q始终在某定直线上.(证明略)
这两个问题可以让学生进行自主思考,学生在积极思考以及方法的比较与筛选中会对运用的知识与方法形成有效的巩固,寻求本源且优化思维的效果也会在这一过程中顺利达成.因此,本课的解题教学不应只有问题1这一道例题,教师在问题1的具体教学中也应引导学生在自主探索、小组讨论、踊跃展示以及师生互动中展开问题的探索与思考,而且还应在此基础上辅助问题2与问题3以令学生得到知识的巩固与能力的锻炼.
学生在已有知识、能力与经验的基础上主动获得知识才是建构主义理论下学习的真正内涵,因此,教师在具体教学中始终应从学生的角度出发并引导学生自主分析与解决问题,使学生能够在解题中充分暴露自己的思维并激发出更多的解题灵感,那些遵循答案走“过场”的解题教学往往无法实现学生思维的探索、重组与优化.H
