圆锥曲线备考方略——观考点，析考题，明考向

☉江苏省如皋市搬经中学 沈 俊

圆锥曲线是每年高考的重点，大约占总分的13%.大多数情况下每年有两道题，一道填空题，一道解答题.圆锥曲线的内容虽然比较多，涉及的知识面也比较广，但它的基本题型还是有“迹”可循的，考查的角度主要涉及以下几个方面：圆锥曲线的定义；圆锥曲线的方程及基本量；直线与圆锥曲线的位置关系；圆锥曲线的实际应用问题等.

一、圆锥曲线的定义

圆锥曲线的定义尽管简单，但意义很重要，是推导标准方程和研究几何性质的基础和根源，高考常常涉及，在近年各省高考试题中都有体现.回归定义和有意识地利用定义是同学们需要加强的一个认识和环节.把握圆锥曲线的定义可以从两个方面入手，即定义表达式和限制条件.

例1 已知F1，F2是椭圆椭圆上任意一点，且∠F1PF2=60°，则△F1PF2的面积为______.

解：如图1所示，设|PF1|=m，|PF2|=n.

根据椭圆定义有m+n=20.

在△F1PF2中，由余弦定理，得|F1F2|2=m2+n2-2m·n·cos60°.

又因为a=10，b=8，

所以|F1F2|=2c=12.故m2+n2-m·n=144，

则（m+n）2-3m·n=144，得202-3m·n=144.

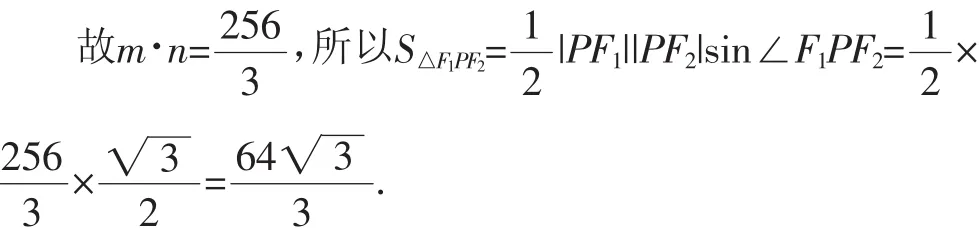
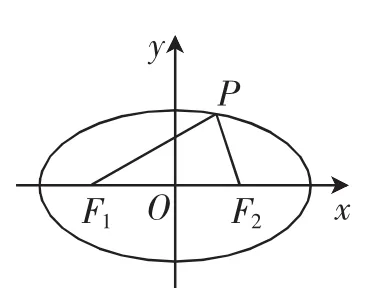
图1

点评：定义是解决一切数学问题的重要理论依据.椭圆、双曲线、抛物线其本质是“一个动点到定点和定直线的距离之比是一个常数的轨迹”.在熟练掌握定义本质的基础上，深入把握其内涵与外延，才能有效快速地运用定义进行解题.

二、曲线的方程和基本量

圆锥曲线方程和几何性质是圆锥曲线部分考查的核心，探究几何性质往往与定义、标准方程相联系.圆锥曲线的离心率、焦点是考查的热点，深刻理解并灵活掌握几何性质是解题的关键.

分析：先寻求问题涉及的基本量，将其化为曲线方程的范围问题，再利用所求的范围来探求离心率e的范围.

解：设Q（x，y），A（-a，0），B（a，0）.

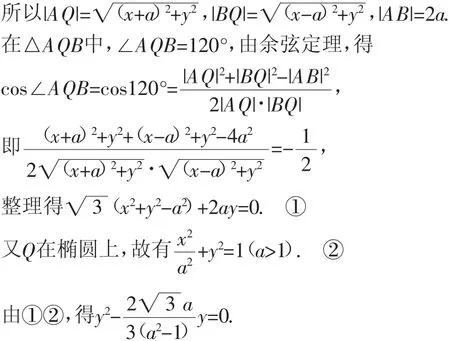
因为y≠0（当y=0时，点Q与A或B重合），

点评：掌握圆锥曲线各量的几何意义，充分利用它们的几何位置关系，是解决这类题目的关键.对于求圆锥曲线离心率的范围问题，充分利用圆锥曲线自身的范围是解决问题的方法之一，要根据圆锥曲线自身的范围建立相应的不等式，从而求出参数的取值范围.在没有限制条件下，椭圆的离心率满足01，抛物线的离心率e=1.

三、直线与圆锥曲线的位置关系

题中常涉及线段的垂直、中点、弦长等，在分析和解决问题时，要将韦达定理、弦长公式、数形结合、设而不求等思想方法综合考虑.因此，要注意归纳与提炼数学思想方法，以快速达到优化解题的成效.

例3 已知直线y=（a+1）x-1与曲线y2=ax有且仅有一个公共点，那么实数a的值为______.

分析：判断曲线y2=ax是否是抛物线，当a=0时，是直线y=0；当a≠0时，联立直线与抛物线组成的方程组进行求解.

点评：在解题中，一方面学生常忽视a=0的情况，误以为y2=ax就是抛物线；另一方面不讨论二次项系数

四、实际应用型问题

实际应用题是高考必考内容，且常考常新，其对学生创新意识和能力的培养具有重要作用.在解答圆锥曲线应用题时一般分为四个步骤：

步骤1：审题；

步骤2：建模；

步骤3：数学问题求解；

步骤4：回答实际问题.

例4“神舟”五号载人飞船进入的预设轨道是以地球的中心F2为一个焦点的椭圆.如图2，椭圆的中心在原点.设近地点为A，远地点为B，地球半径为R.

（1）从数学角度分析，仅知道近地点A的高度m，能否确定飞船飞行的椭圆轨道的方程？如还知道远地点B的高度n呢？

（2）已知m与n，求飞船飞行的椭圆轨道的方程.

（3）若m=200公里，n=350公里，已知地球半径R＝6371公里，求飞船飞行的椭圆轨道的方程.

分析：在熟悉了科学背景与一些常用名词后，熟练运用椭圆的相关知识进行求解即可.

解：（1）如仅知道近地点A的高度，不能确定飞船飞行的椭圆轨道的方程；如还知道远地点B的高度，则可以确定飞船飞行的椭圆轨道的方程.

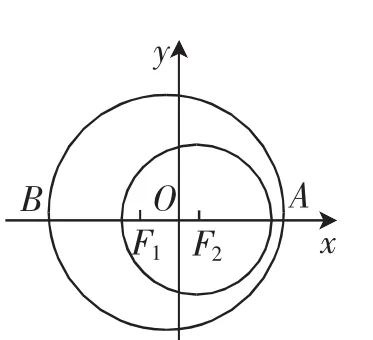
图2

（3）因为m=200公里，n=350公里，R＝6371公里，将其代入（2）中的方程，解得飞船飞行的椭圆轨道的方程为

点评：圆锥曲线与实际生活有着千丝万缕的联系，如人造地球卫星的轨道是椭圆，双曲线时差定位法在国防、军事、航天、救灾抢险等方面有着重要的运用，抛物线也是航天中发射与回收抛物体的运动轨迹.

在圆锥曲线的学习中要注意领会培养、强化提高解析几何内容渗透出的数学思想和方法.比如分类讨论、函数与方程、等价转化、数形结合等数学思想，以及坐标法、定义法、整体处理法、配方法、换元法、待定系数法、参数法等数学方法.注意训练通法，养成良好的思考问题的习惯，以及注重解题途径和方向的选择.这不但能使问题快速得解，而且能活跃同学们的数学思维.H