优化高中数学解题方法——以填空题为例

☉江苏省无锡市湖滨中学 吕 娉

高中数学考试中涉及多个考试项目，填空题是其中最为重要的一部分，虽没有选择题的选项优势，也没有解答题要求的逻辑性，但填空题具有其独特的解题魅力.填空题的解题方式的难易程度应学生个人的数学素养而异，无论哪种解题方式，其主要目的都是获得最后正确的答案，对此在做题中要选择正确无误的解题方式.本文以数学填空题的解法为出发点，从不同的角度分析数学的奥秘，从而变枯燥乏味的数学解题过程转化为以兴趣为主的学习过程.

高中数学作为高中必修科目，为升入理想的大学，学生需要不断地练习各种题型的数学题，其中不乏机械性的学习和讲解，进而使原本活跃的学习气氛化为枯燥的做题训练场.处于这个环境下的学生，学到的数学知识无法充分应用于实际生活.对于数学基础知识的学习时间长，所取得的学习效率普遍较低，长此以往，学生对数学产生厌倦情绪.虽然高考数学试题相对较难，但其所陈述知识点多数来源于课本知识的拓展.对此在学习中要充分发挥试卷的潜能，准确地记忆试题中涉及的知识点，将“难上天”的数学题简单化，进而使我们在复习中也更加轻松.

本文主要从以下几个方面介绍数学填空题的做题方法.

一、直接法

所谓直接法就是根据题目所给的条件，运用以往学到的知识点，概括性地总结分析题中设计的知识点，最后得出正确结果.这种方法相对较为简单、直接，是一种通过现象看本质的最佳方式.

例1 已知数列{an}为递增的等差数列，当a1＝1，a3＝a22-4，则an＝______.

解析：设等差数列{an}的公差为d，则由a3＝a22-4，

得1＋2d＝（1＋d）2-4，

所以d2＝4，所以d＝±2.

由于{an}为递增数列，

所以d＝2.

所以an＝1＋（n-1）×2＝2n-1.

探究提高：该题为典型的等差数列，运用直接法来解答，利用等差数列的通项公式和性质，继而计算出等差数列的相应参数，是直接法运算的典型，计算相对较为简单明了.能根据题目中给出的信息看到解题的本质，因此在解题中相对较为简单.

二、特殊转化法

特殊转化法作为一种特殊的计算方法，其运算的原理是将一个运算利用它们之间的关系转换为另一种方法进行计算的方式，运用这种方法不仅能够极大地缩短做题时间，同时精准度也有所提升，与其他解题方法相比，该方法方便简明，是解决填空题的最佳方法.

例2 如图1，图中是由三个等半径的圆相交于一点P形成的（点P不在C上），内部相交部分为虚线相连，外部实线的三个圆弧组成曲线C，假设圆弧上第i段弧所对应的圆心角为αi（i＝1，2，3），

图1

解析：本题可从三个等半径的圆所构成的等边三角形为出发点求解.（取特殊位置）

根据题意知，三段圆弧构成一个等边三角形，

则∠O1O2O3＝∠O2O1O3＝∠O2O3O1＝60°.

根据上述得，实线三段圆弧所对应的圆心角α1＝α2＝α3＝240°，

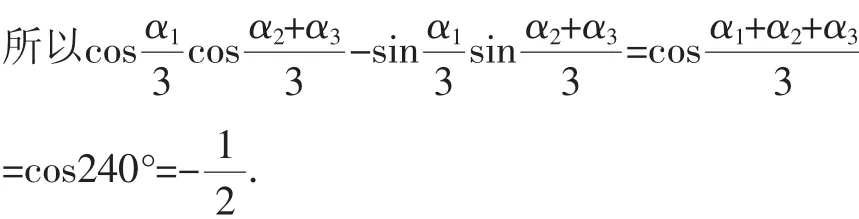
探究提高：由于特殊转化法较为简单，做题准确率也较高，在高中数学试题练习中是最常用的方法.主要用于存在某些不定量元素的填空题中，倘若填空题中具有一定的数值和结论时，在解题过程中，可采用特殊转化法，将题中不定量运用其他的特殊值进行处理.从而在较短时间内，做出相应的数学答案.

三、构造法

构造法是高中数学填空题中较为特殊的一种解题方法，其做题的简易程度因题而已，根据不同的题型选取不同的构造方法，才能变复杂为简单.运用此种方法，可根据已有的条件，构建出新式数学模型，来解答数学填空题.

解析：根据题意直接求函数f（x）的最大值与最小值相对较难，且计算量较大，而将函数进行化简可形成一个新的函数.化简过程如下：

再利用函数g（x）的奇偶性求解函数f（x）的问题.

根据上述得g（x）=f（x）-1为奇函数，

则m-1=-（M-1），所以M+m=2.

探究提高：从函数题的整体出发，进行思考运用函数的奇偶性特征进行解题，是一种利用整体来构思的方式.解题过程中运用了分式类函数的结构特性，通过与分式函数的最值相联系，最终实现解题的方式.其中部分分式转变变形为奇函数.利用构造法解题，来处理最大值与最小值这类问题，将复杂的数学问题分析透彻，进而使做题更加简单化.若想要更加方便地运用构造法解决数学问题，需要我们熟练地掌握函数的基本性质以及运用原则.

构造法解答这类数学问题，需要学生具有极强的数学模式思维，以在脑海中形成明晰的解题思路.

四、数形结合法

数形结合解题方法就是将数学试题中提到的条件和有用信息，通过图形的方法展现出来，通过图形能够明确地看出它们相互之间的关系，便于学生理解和解题思维的构建.利用数形结合的类型在高中数学习题中较为常见，且方法多样.

例4已知函数f（x）为奇函数，定义域为R，满足f（x-4）=-f（x），且函数在定义域［0，2］上为增函数，若方程f（x）=m（m>0），在区间［-8，8］上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4=______.

解析：根据题意可知，f（x）为奇函数，定义域为R，且满足f（x-4）=-f（x），所以f（4-x）=f（x）.因此，f（x）函数图像关于直线x=2对称，且f（0）=0，由f（x-4）=-f（x）知，f（x-8）=f（x），可得函数周期为8.

又因为f（x）在区间［0，2］上是增函数，所以f（x）在区间［-2，0］上也是增函数，则方程f（x）=m（m>0）在区间［-8，8］上有四个不同的根x1，x2，x3，x4，可设x1

探究提高：以上是典型的数形结合题，相对较为简单，但容易出错，因此在做题中需要仔细检查.

当前有许多高中依然采用机械的方法——大量地刷新题库，在这种教学方式下，学生思维僵化而无创新能力，学习场转变为做题训练场.高中阶段是我们知识增长的关键阶段，因此要合理地运用课外教材，将学到的数学知识与生活实际相结合，转化思维方式，运用多样的做题方法，探索数学中最深处的知识内涵，体会高中数学的魅力，化被动的接受为主动的接收，创建符合高中生最实际的解题平台，为高考奠定坚实的基础.H