高中数学教学中设问、追问与点拨的实践思考

☉江苏省盐城市伍佑中学 高小勇

新课程的教学观一直将课堂教学看成教与学、师与生的交往，教师在师生双方的交流、沟通、启发与补充中成为了现代学生发展的促进者.笔者近期听了一节“函数的奇偶性”并产生了一点体会，现结合新课程的教学观以及听课中的感悟谈谈自己的一点看法.

片段1.课堂导入与概念生成环节中的设问

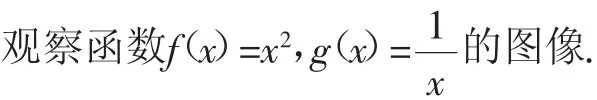
问题1：f（x）=x2的图像是什么对称图形？

问题2：求f（1），f（-1），f（2），f（-2），推广到a∈R时，求f（a），f（-a），它们之间的关系如何？

生1：f（x）=x2的图像是轴对称图形.

生2：f（1）=1，f（-1）=1，f（2）=4，f（-2）=4，f（a）=a2，f（-a）=（-a）2，f（a）=f（-a）.

师：回答得很不错.（随即给出偶函数的概念）

教师在片段1中设计了问题串来帮助学生对函数奇偶性的定义和判断方法进行了思考和归纳，从特殊到一般和数形结合的思想也是教师在问题串的设计力图渗透的，教师的立意很好，不过笔者以为问题的设计上还有需要改进的地方：

（1）教师的问题设计虽然考虑到了学生的最近发展区，但学生在问题上并没有获得教师预期的发展，举例活动虽然令学生对对称这一知识点进行了回顾，但甚为简单的两个问题却令学生的思考意义不大，新的感悟和收获并不能有效产生.学生在初中阶段学习过点与点关于x轴、y轴、原点对称的性质，因此，我们是否可以考虑到学生的这一认知基础并在设计问题时将y=x2关于y轴对称、对称点的坐标关系、输入值的关系、输出值的关系等内容突出体现呢？使学生从区别于初中所学的高度入手展开思考与研究.

（2）问题太过简单，学生在一看就知道答案的问题面前往往无需太多的思考，教师如果在问题的设计上能

师：中心对称、轴对称是我们同学初中时候学过的两个知识点，大家能举出反映这两个知识点的生活实例吗？

学生举出了黑板、板凳、眼镜等实例，发言表现踊跃.

师：数学中的对称大家留意过吗？我们来看一下.够注意到难度的递增将会令学生的思考产生更大的动力.学生在问题2的解决中也只是做了几道简单的算术题，学生的思维没有积极性可言.

（3）问题的最终答案与课堂所学概念之间的衔接不够自然，生硬的链接无法体现问题的设计功能.学生经历问题2的解答至概念的引入环节过程给人一种生拉硬拽的感觉，概念的出现也就显得较为突兀了.从本质上来讲，着眼于形的观察与数的验算的两个问题之间并没有有机结合，学生对数形结合思想的体会也就成了一种形式.学生在问题的回答中是否真正获得了知识发生、发展的体验是一个令人质疑的问题，对于数学思想方法的体会也一样值得商榷.

片段2.概念剖析中的追问

师：请大家对两个定义进行观察并分析一下两个函数都有哪些共同点和不同点.

生3：两个定义中都有“定义域中每一个x”的字样是其共同点；f（x）和f（-x）的关系一正一反是其不同点.

师（追问）：f（x）和f（-x）中x和-x的大小关系如何呢？

生3（犹豫良久）：不知道.

（教师喊了另一位学生）

生4：当x=0时，x=-x；当x＞0时，x＞-x；当x＜0时，x＜-x.

师（追问）：x和-x在数轴上有怎样的关系呢？

生4：x和-x是关于原点对称的.

师（有点着急）：那你可曾看出奇函数、偶函数的定义域应该满足哪些条件呢？

生4（稍作思考）：定义域为R.

师：那么定义域是不是一定要为R呢？

生4：不一定.

师（语气强烈并将手指指向了“关于原点对称”几个字）：为什么？

生4：只要满足关于原点对称就行.

教师随即给出了奇函数、偶函数的定义域关于原点对称的注释，并指出函数的定义域若不关于原点对称则其便不具备奇偶性.

教师在片段2的教学中尝试运用一系列的追问来引导学生进行本课核心内容的思考，但明显没有充分考虑学情的问题设计显得抽象且不利于学生思考.教师在学生理解概念的设计中可以将鲜活的事例引进课堂来帮助学生在具体形象的情境中进行抽象，而不是一味依赖教师的语气或暗示来强迫学生回答，教师追问时明显的情绪化导向往往会令学生得不到正确答案时便立即换答案，这种不能及时修正学生思考方向的追问往往会给学生拷问犯人的感觉，学生在面对教师的提问时产生诚惶诚恐的情绪也变得很正常了.因此，笔者以为教师在设计问题时应考虑学情以及问题呈现的直观性与生动性，同时还应表露出积极的、鼓励性的情感，具体表现在：（1）尊重学生的答案并促进学生连贯性的思维；（2）与学生建立平等交流的互动并充分考虑学生的主体地位；（3）给予学生充分的思考时间并不断激励学生探索与求知.教师在具体教学中如果能做到这几点，学生必然能真正感受愉悦的情感并作出更加积极的应答.

片段3.教师在学生回答上的点拨

例题讲解之后，教师投影了以下练习并请两名学生将解答板书在黑板上.

已知下列函数，请判断其奇偶性：

①f（x）=x2-1；

②f（x）=（x-1）2，x∈［-1，1］.

生5对②的判断是：既不是奇函数也不是偶函数，因为该函数的定义域不关于原点对称.生6则对②进行了如下解答：定义域关于原点对称，f（-x）=（-x-1）2=（x+1）2≠（x-1）2=f（x），f（-x）=（x+1）2≠-（x-1）2=-f（x），因此f（x）既不是奇函数也不是偶函数.

教师对两位学生的解答分别作了点评，首先在数轴上直接标出了区间［-1，1］并引导学生进行观察、点评生5的解答.点评生6的解答时则首先提出了疑问.

师：大家觉得生6的解答对吗？比如，当x=0时，f（-x）≠f（x）是不成立的.

师：还有更好的解法吗？大家可以讨论一下.

（几分钟后）

生7：我认为可以利用图像，f（x）=（x-1）2，x∈［-1，1］的图像的对称轴为直线x=1，不是y轴，因此不是偶函数，而且我们观察也可以发现，图像也是不关于原点对称的，因此也不可能是奇函数.

师：解答题中一般不运用图像解题，还有其他方法吗？

（几分钟过后，仍没有学生应答）

师：偶函数的定义中强调f（-x）=f（x）应对定义域内每个x都成立，举出一个特殊的例子来说明其不成立即可解得此题.我们可以运用取特殊值的办法：f（1）=0，f（-1）=4，f（1）≠f（-1），由此可以说明f（x）是不具备奇偶性的.

教师对生5的点评中没有体现出教师对学生具体想法的思考.生6的解答虽然是教师预设的解法，但教师并没有对学生的思维火花进行发现.对生7的点评更加简单甚至还犯了错误，生7的解答虽然是错的，但其思考的方向却能给学生别样的思考，但教师对其解答的处理却令学生错失了一个很好的机会，这显然是教师备课不充分导致的.教师的主观意识上必然还存在着以教师思路为主的错误思想，这种错误思想往往会导致教师在课堂教学中无法把握点拨学生的时机与具体方法.事实上，教师在具体教学中一定要重视以下几个方面：（1）备课时一定要充分考虑学生课堂学习时可能的反应，要预想出现情况时的应对方法；（2）要及时发现学生思维的价值，对学生进行及时而恰当的点拨并促进学生思考得更加完整；（3）教师在引导学生思考与探索时要善于运用四两拨千斤的教学艺术；（4）把握设问、启发、点拨的时机并做到不愤不启、不悱不发.

本节课的执教老师可能因为课堂驾驭能力的欠缺而导致设问、追问、点拨各环节显得生硬而粗糙，学生的思维也没有得到真正有效的激发.我们教师在自己的教学或者听课活动中应善于反思，对设问的设计、追问的艺术、点拨的技巧等各个环节进行仔细的考量与斟酌，使自身的教学技艺在长期的实践、反思与修炼中不断成长.W