不确定线性时滞系统的有限时间鲁棒无源控制
2018-11-16吴保卫
王 欣, 吴保卫
(陕西师范大学 数学与信息科学学院,西安 710119)
在许多工程问题中,稳定性研究常常和系统的耗散性理论相结合.耗散性是指动态系统内部的能量消耗小于外部供给的能量[1].作为系统耗散性概念的一个特例,无源性不仅是系统的一个重要性质,而且是控制系统的重要途径.
无源性理论由Willems在1972年首次提出,后由Hill和Moylan于1980年加以推广[2-3].近年来,无源性分析和基于无源理论的控制设计逐步发展起来,在线性和非线性系统的控制设计和分析中发挥着重要的作用[4-6].
在系统的收敛性分析中,有几类经典的稳定性概念.例如,李雅普诺夫稳定性、渐近稳定性、有界输入有界输出稳定性.这些概念定义在无限时间区间上并且表明了动态系统的定性行为.然而,在实际应用中,给定初始条件约束,总是希望动态系统的状态不超过某个阈值.因此提出了有限时间稳定的概念.目前,鉴于线性矩阵不等式理论的发展,有限时间稳定的概念重新被研究并取得了很多新的成果.文献[7]利用李雅普诺夫函数结合线性矩阵不等式方法对一类连续和离散系统的有限时间稳定和镇定问题进行了讨论.文献[8]首次解决了一类不确定脉冲动态线性系统的鲁棒有限时间稳定问题,并给出了基于严格线性矩阵不等式表示的保证系统有限时间稳定的充分条件.
时滞在实际系统中广泛存在[9-10],它可以降低控制系统的性能甚至使系统不稳定.因此,研究不确定时滞系统的无源控制问题得到了许多学者的关注.文献[11]讨论了一类具有状态时滞的不确定奇异系统的鲁棒无源问题;文献[12]研究了离散切换时滞奇异系统的有限时间H控制,该条件与时滞大小无关,因而具有较大的保守性;文献[13]分析了具有时滞依赖马尔可夫跳跃系统有限时间H控制;文献[14]解决了一类具有时滞的不确定非线性系统的有限时间鲁棒无源控制问题.
本文通过构造无记忆状态反馈控制器解决了一类不确定时滞线性系统的有限时间鲁棒无源控制问题.引入新的积分不等式解决了李雅普诺夫函数的求导问题,以线性矩阵不等式形式得到的充分条件保证了闭环系统是有限时间有界并且满足给定的无源指数.
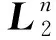
1 预备知识和问题描述
考虑下面不确定时滞系统:
y(t)=(C+ΔC)x(t)+(C1+ΔC1)x(t-τ(t))+(D+ΔD)u(t)+(D1+ΔD1)ω(t)
x(t)=φ(t),t∈[-τ,0]
(1)
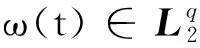
其中,R1,R2,S1,S2,S3,S4是已知的实常矩阵,F是具有Lebesgue可测范数的实不变未知矩阵,且满足FTF 考虑状态反馈控制器:u(t)=(K+ΔK)x(t),ΔK是扰动矩阵,ΔK=GFcHK,其中G,H是已知的实常矩阵,Fc是未知矩阵,满足FcF≤I. 由系统与状态反馈控制器构成的闭环系统为: x(t)=φ(t),t∈[-τ,0] (2) 定义2[16]对于系统(1),状态反馈控制器称作具有耗散率η的有限时间无源控制器,如果闭环系统(2)是有限时间有界的,且存在正实数η,使 引理1[17]设X,Y,ε分别是已知常矩阵与任意正实数,则有 XTY+YTX≤εXTX+ε-1YTY. (1)S<0; 引理3[19]对于任意的常矩阵N1,N2∈Rn×n,L∈Rn×p,正定对称矩阵Z∈Rn×n和时变时滞τ(t),有: 其中: 定理1 对于δ,c1,T,ω>0和正定矩阵Rc,闭环系统(2)关于(c1,c2,ω,T,Rc)是有限时间有界的,如果存在常数c2>0,正定矩阵Pi(i=1,2,3)和任意矩阵N1,N2,L,使得 其中,Ξ和Y在引理3中被定义,且有: 证明选取以下Lyapunov-Krasovskii函数 V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))= 对V(x(t))求导得: δωT(t)ω(t)≤ ξT(t)[Θ1+τΛTP3Λ+τYTP3-1Y]ξ(t) 上式两边积分有: 且 故 因为 所以 由定义1可知系统是有限时间稳定的. 定理2 对于δ,c1,T,ω>0和正定矩阵Rc,闭环系统(2)关于(c1,c2,ω,T,Rc)是有限时间有界且是鲁棒无源的,如果存在常数c2>0,β>0正定矩阵Pi(i=1,2,3)和任意矩阵N1,N2,L,使得 其中: 证明选取和定理1相同的Lyapunov-Krasovskii函数 因此,由定理条件和Schur补引理可得: 上式两边积分可得: 故 其中: σRc-1 则得到了鲁棒有限时间无源控制器:K=YX-1. 证明选取和定理1相同的Lyapunov-Krasovskii函数V(x(t)),根据引理3,定理2,我们可得如下的关系: 其中: ψ11=(A+BK)TP1+P1(A+BK)+P2-δP1+N1T+N1 φ11=ΔATP1+P1ΔA+ΔKTBTP1+P1BΔK+P1ΔBK+KTΔBTP1T+P1ΔBΔK+ΔKTΔBTP1 φ13=P1ΔB1-ΔCT-ΔKTDT-KTΔDT-ΔKTΔDT φ14=τ(ΔAT+ΔKTBT+KTΔBT+ΔKTΔBT) 上式可等价为 Ω2=Σ+W1FW2T+W2FTW1T+W1FW3T+W3FTW1T+W4FcW5T+W5FcW4T<0 由引理3,上式对所有满足FTF≤I,FcTFc≤I的不确定矩阵F,Fc成立,当且仅当存在常数η1>0,η2>0,η3>0使得 Σ+(η1+η2)W1W1T+η1-1W2W2T+(η2-1λ5+η3-1)W5W5T+η3W4W4T Σ322=diag[-(η1+η2)-1I,-η1I,-η3-1I,-(η3-1+η2-1λ5)-1I], 其中: 本文研究了不确定时滞线性系统的鲁棒有限时间无源控制问题.通过使用无源控制理论和李雅普诺夫函数方法,得到的时滞依赖充分条件使得闭环系统满足有限时间有界性和无源性条件.基于理论条件,通过求解线性矩阵不等式可以得到控制器的设计方法.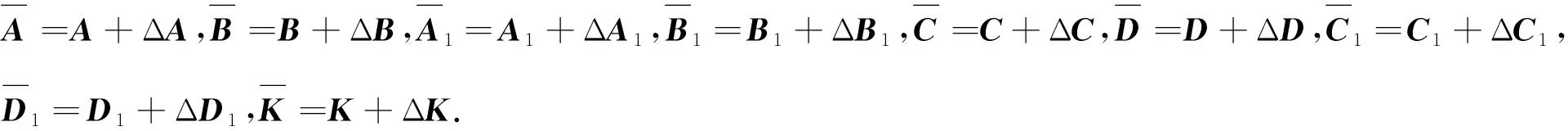
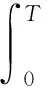

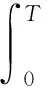
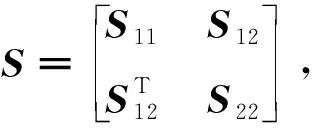
2 主要结果
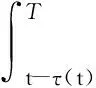
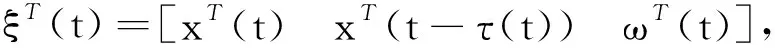
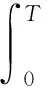
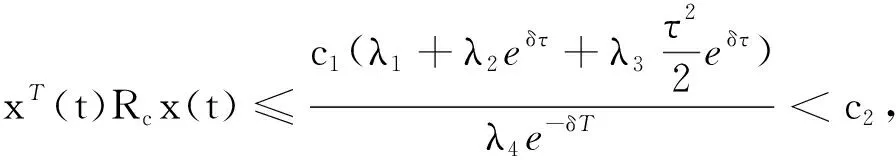


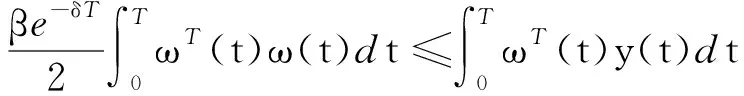
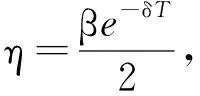

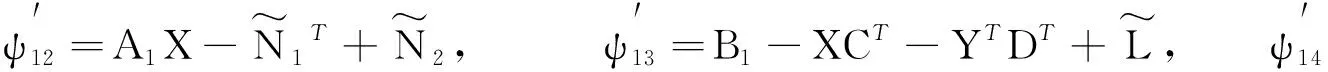
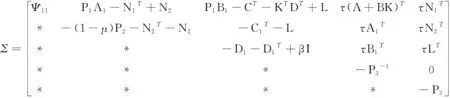



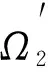
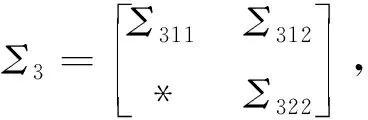
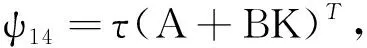
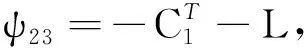

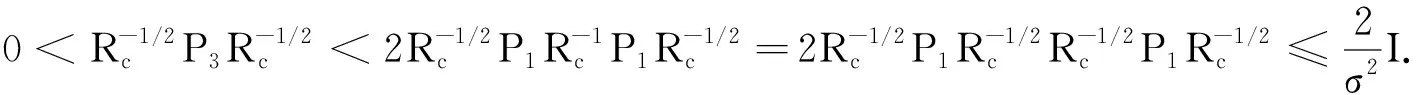
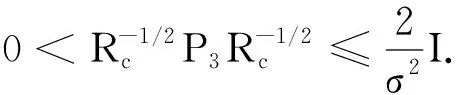
3 结论
