基于演化博弈的港口竞合策略选择及仿真研究
2018-11-15赖成寿高天航
赖成寿,吕 靖,李 慧,高天航
(1. 大连海事大学 交通运输管理学院,辽宁 大连 116026; 2. 大连理工大学 管理科学与工程学院,辽宁 大连 116024)
0 引 言
现阶段面临“量价齐低”的市场环境,港口通过合作获得收益远高于企业恶性竞争时的收益[1]。港口合作并非由同一主管部门监管,因此合作关系依赖于契约关系维持,但由于信息不对称,均会担心因对方违约而造成己方损失,使合作难以持续开展,导致囚徒困境局面。港口资源整合的长期性和艰巨性决定了港口竞合策略机制选择的重要性。港口合作联盟作为利益导向,参与体随时根据自身利益最大化进行策略选择与调整。整体合作收益最大化与港口单一自身收益最大化的目标不一致导致港口合作违约情况加剧,产生港口恶性竞争,解决途径并非全盘否定个体理性,而需要对港口行为策略选择的内在机理和发展规律进行探究,引导港口间协调合作。
相关学者主要从港口合作的有效性、港口整合模式、合作途径、合作收益分配的角度进行研究。G. FRANKELE[1]分析得出竞争环境中港口合作的必要性;W. K. TALLEY等[2-4]的研究指出:海上运输受承运人利润、港口吞吐量以及托运人成本限制等因素影响,论证合作港口服务链比非合作更有效;YANG Yan等[5]提出了港口的多种整合模式;丁荣涛[6]通过建立云模型,解决了港口供应链上资源和协作组织的选择问题;王景敏[7]就港口供应链协同机制构建提出建议。T. W. LEE等[8]提出港口协作的方式和途径,并建立了网络模型评估港口供应链绩效;P. FRANC等[9]认为:要提高港口竞争的关键因素在于整合海运和内陆运输链能力;陈军等[10]建立博弈决策模型和集中式决策模型讨论供应链服务合作策略。赖成寿等[11]和M. C. B. CHENG等[12]分别提出港口合作的收益分配改进方法。
相关学者的研究为港口竞合行为策略选择奠定了基础,但存在以下不足:①大都从宏观角度分析,缺乏从微观分析内在机理;②均以静态分析为主,缺乏对港口间竞合关系变化的长期动态规律研究;③基于完全理性、充分信息、有限参与者假设的博弈方法,难以刻画出港口相互学习、模仿、竞合策略行为选择的过程,对解释港口间合作机制具有一定局限性。
港口策略选择过程中受诸多因素影响及其复杂性,决定了港口具备明显的有限理性特征;同时,由于港口合作参与体的差异会致使收益、成本等均会有所不同,若将港口行为放大到多规模群体,合作关系将变得复杂和不确定;更重要的是,港口策略选择会受市场环境影响而呈现动态竞合关系。演化博弈论摒弃超理性假设,以有限理性为基础,将博弈分析和演化动态有机地结合起来,强调均衡是学习调整的结果而不是选择的结果,考察经济现象剖析微观复杂经济系统[13]。鉴于此,为有效刻画港口竞合策略选择的动态演化博弈过程,笔者选择演化博弈方法来探讨涉及因素对港口竞合策略选择的机制,依托港口间竞合博弈模型的输出,针对港口竞合策略涉及微观层面因素,分析其对港口竞合策略选择动态趋势的影响,定量分析了港口竞合策略选择的内在机理,揭示了港口竞合关系发展演变的客观规律。
1 港口竞合博弈及演化模型构建
通过构建港口竞合博弈模型,求解完全竞争、竞合并存、完全合作这3种情形下的均衡价格和收益,并基于shapely值对联盟收益进行分配。以模型输出结果,并引入“合作成本”、“违约收益”、“违约补偿金”,构造演化博弈支付矩阵,建立两港口间演化博弈模型。
1.1 港口竞合博弈模型构建
为便于建模,做如下假设:决策主体中含n个港口,港口可实施差别费收策略,港口服务无差异;港口初始市场需求确定,需求具有价格弹性;个体理性且都有决策权利,追求自身收益最大化。
港口i作业量的Di是pi和pj的函数,即需求受自弹性和交叉弹性共同影响,需求函数如式(1):
(1)
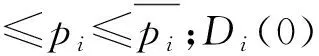
港口i的收益如式(2):
πi=(pi-vi)Di-fi
(2)
式中:vi为港口i的单位成本;fi为港口i的固定成本。
1.1.1 完全竞争情形
港口i追求最大化自身收益,如式(3):
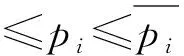
(3)
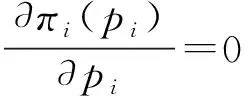
(4)
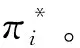
1.1.2 港口部分合作情形
港口i通过与部分港口组成的系统为:N1={1, 2, …,n1},其目标是实现总收益最大化;不在系统中的港口j∉N1追求自身收益最大化,选择合作的港口收益i均不低于完全竞争情形,如式(5)。
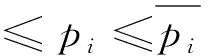
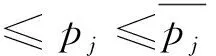
(5)
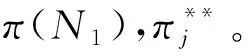
1.1.3 完全合作情形
港口均追求整体N={1, 2, …,n}的收益最大化,合作后整体或部分收益不低于完全竞争和竞合并存情形,如式(6)。
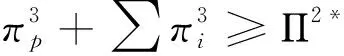
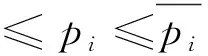
(6)
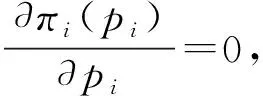
(7)
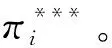
1.2 港口演化博弈模型构建
构建港口演化博弈模型,做如下假设:博弈方两港口均符合理性人的假设,都追求自身利益最大化,但在演化过程中,做不到完全理性。
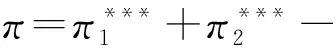
行为策略及比例:两港口均存在合作和竞争两种策略,设港口1、2选择合作的概率分别为x=x(t),y=y(t),则选择竞争的概率分别为1-x=1-x(t),1-y=1-y(t),两港口进行演化博弈支付矩阵如表1。

表1 港口进行演化博弈支付矩阵Table 1 Port payoff matrix of evolutionary game
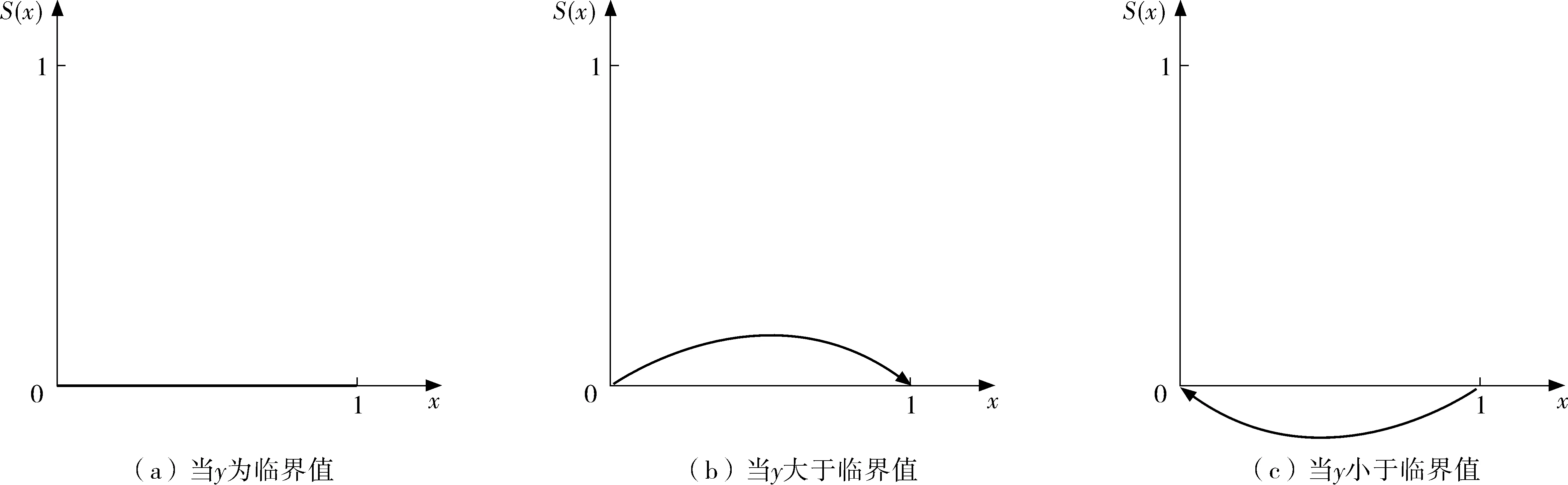
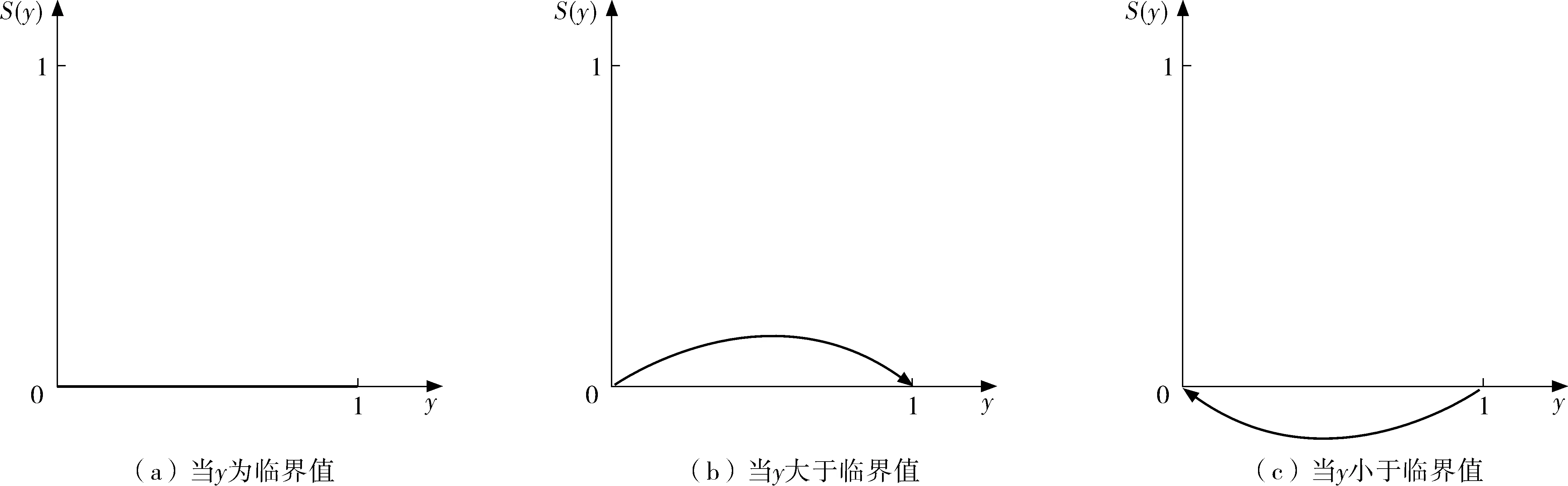
现实中,采取合作的双方总收益均大于其中一方选择竞争的收益和,即有:rπ>n1,π(1-r)>n2,π>n1+n2;同时,违约惩罚一般不会超过双方在博弈中的损失,即β 合作主体随时根据自身利益最大化进行竞合策略选择和调整,故港口间博弈是一个长期重复的动态博弈过程,双方通过不断学习和模仿将稳定策略传递到后续博弈中,以获得稳定收益。为方便分析,a表示港口1,b表示港口2。 港口1选择合作的收益如式(8): (8) 港口1选择竞争的收益如式(9): Ua1-x=(u-α+n1-β)y+u(1-y)=-αy+ n1y-βy+u (9) 港口1的混合策略的平均期望收益如式(10): (10) 港口1复制动态方程如式(11): (11) 图1 港口1演化博弈的动态相位图Fig. 1 Dynamic phase diagram of evolutionary game of port 1 港口2选择合作的收益如式(12): (12) 港口2选择竞争的收益如式(13): Ub1-y=(v+n2-β)x+v(1-x)=(n2-β)x+v (13) 港口2的混合策略的平均期望收益如式(14): (14) 港口2的复制动态方程如式(15): (15) 图2 港口2演化博弈的动态相位图Fig. 2 Dynamic phase diagram of evolutionary game of port 2 根据该系统对应雅克比矩阵J的行列式De(J)及其迹Tr(J)判断港口竞合的稳定均衡性,如式(16)~(18)。 (16) (17) (18) 其中: 均衡点的稳定性计算结果见表2。 表2 局部均衡点的行列式D和迹T的表达式Table 2 Local stability analysis of system equilibrium points 其中: t1= t2= 由均衡点的行列式De(J)和迹Tr(J)的计算结果可看出:系统存在两个演化均衡点E1(0, 0),E4(1, 1);两个不稳定均衡点E2(0, 1),E3(1, 0);以及一个鞍点E5(x1,y1)。港口间的动态演化见图3。 图3 港口1、2的动态演化相位图Fig. 3 Dynamic phase diagram of port 1 and port 2 由图3可知:港口演化博弈路径和结果取决于参与双方的初始状态以及鞍点位置。当初始状态坐标(x0,y0)落在A区域,博弈双方最终会演化到均衡点E4(1,1),最终双方均会选择合作策略;当(x0,y0)落在C区域,博弈双方最终会演化到均衡点E1(0,0),最终双方会选择竞争策略;当(x0,y0)落在B区域或D区域,此时的博弈演化方向就难以确定,均衡点可能为E1(0,0)也可能为E4(1,1),具体走向需借助信息引导。 通过演化博弈模型结果可看出:港口竞合策略演化的长期均衡结果可能是双方竞争,也可能是双方合作。在长期演化过程中,港口收敛均衡点以及演化路径受初始状态的选择、合作收益增量π、收益分配比例r、受背叛方损失m、背叛方利益n和因违约处罚金β的影响。以下讨论各参数变化对演化博弈稳定策略的影响。 收益增量π和违约金β增加时,鞍点E5就会向原点E1(0,0)靠近,区域A的面积会变大,动态系统中的博弈双方收敛于均衡点E4(1,1)概率也将增加;合作收益分配比例系数r增加时,鞍点E5坐标向右下方移动,区域A的面积变化不确定,对演化路径和演化结果影响不确定;额外收益n1、n2增加时,鞍点E5就会向E4(1,1)靠近,区域A的面积会变小,博弈双方收敛于均衡点E4(1,1)的概率也将降低;收益损失m1、m2增加时,鞍点E5就会向E1(0,0)靠近,区域A的面积会变大,动态系统中的博弈双方收敛于均衡点E4(1,1)的概率将会增大。 这些因素对演化博弈影响机理主要体现在会影响博弈参与主体的行为,进而影响参与主体的策略选择。收益增量π、违约金β、受背叛方损失m增加和背叛方利益n降低,在合理的收益分配比例r情形下,就会增加选择背叛的“机会成本”,主体就趋向于选择合作,且不会轻易背叛合作。 为更好地描述各参数对港口策略行为选择的影响,笔者对港口演化路径进行了模拟仿真。实验环境为MATLAB R2010b,假设通过1.1节中的模型计算出港口1、2在竞争情形下的收益分别为2 000、1 500万元;在合作情形下联盟总收益为4 200万元;基于Shapley值法,港口1分配收益为2 350万元,港口2分配收益为1 850万元。则此时u=2 000,v=1 500,π=700,r=0.5;另设n1=250,n2=200,α=80,β=60,m1=50,m2=80;显然满足实际情况:rπ>n1,π(1-r)>n2,π>n1+n2,β 图4 港口竞合策略演化路径仿真Fig. 4 The simulation of the evolution path of port co-opetition 由图4可得到:初始比例为(0,0.2),(0,0.4)时,港口1选择策略为竞争;随着港口2选取合作比例越高,港口1合作意识也随之逐渐加强,策略由竞争向合作演化,并最终会选择合作。当初始比例为(0.1,0),(0.3,0)时,港口2选择策略为竞争,随着港口1选取合作比例越高,港口2合作意识随之逐渐加强,其策略由竞争向合作演化,并最终会选择合作。 引起变化临界点为鞍点E5(0.105,0.259),在x∈(0,0.105)∩y∈(0,0.259)区域内,港口策略的均衡点为双方竞争;初始状态在区域范围x∈(0.105,0)∩y∈(0.259,1)中,港口策略演化成双方合作;此外初始状态(x,y)在其他区域,演化博弈结果不能确定,均衡点可能为E1(0,0)也可能为E4(1,1)。 当初始状态为一方选择合作,另一方选择竞争,若合作方承担较大损失,将会通过学习和模仿而选择竞争策略。合作关键在于是否存在较大的违约惩罚以及合作收益分配合理性,否则合作关系的持续性难以为继,易引发恶性竞争。 针对影响演化路径影响因素有:合作收益增量、收益分配比例、受背叛方损失、背叛方利益和因违约处罚金。因此可签订合作协议,通过提高违约“惩罚金”、合作“补偿金”、背叛成本等方式来促成合作,通过设计合理的利润分配方式来增强双方合作满意度促成合作并维持合作稳定。此外,还可通过资本渗透、实行差异化发展功能定位等措施强化合作机制,从而使双方合作成为唯一的进化稳定均衡。但由于系统演化为一漫长过程,因此在相当长的时期内港口会保持竞合共存状态。 我国港口资源整合的长期性和艰巨性决定了港口竞合策略机制选择重要性。基于竞合博弈和演化博弈理论,笔者分析了港口竞合行为策略选择的内在机理和发展演变的规律,并进行仿真分析。结果显示:港口演化仿真结果与演化相位图具有一致性,演化稳定均衡点以及演化路径受初始状态选择、“合作收益增量”、“收益分配系数”、“合作成本”、“违约收益”、“违约补偿金”等影响。针对影响演化路径和策略选择参数提出使双方合作成为进化稳定均衡的措施:提高违约“惩罚金”、合作“补偿金”、背叛成本;设计合理的利润分配方式,资本渗透、实行差异化发展的功能定位等措施,以强化合作机制、维持合作稳定。 笔者为港口竞合行为策略选择提供结构化思考模式,为有效解决合作过程中的信息不对称而易产生恶性竞争这一问题提供分析方法和理论依据。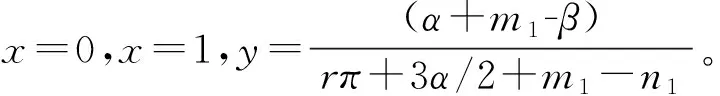
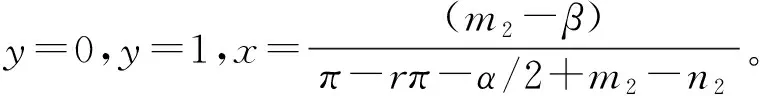
2 双方演化博弈均衡点稳定性分析
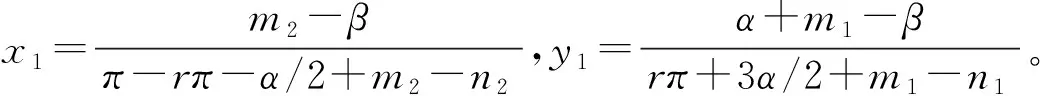

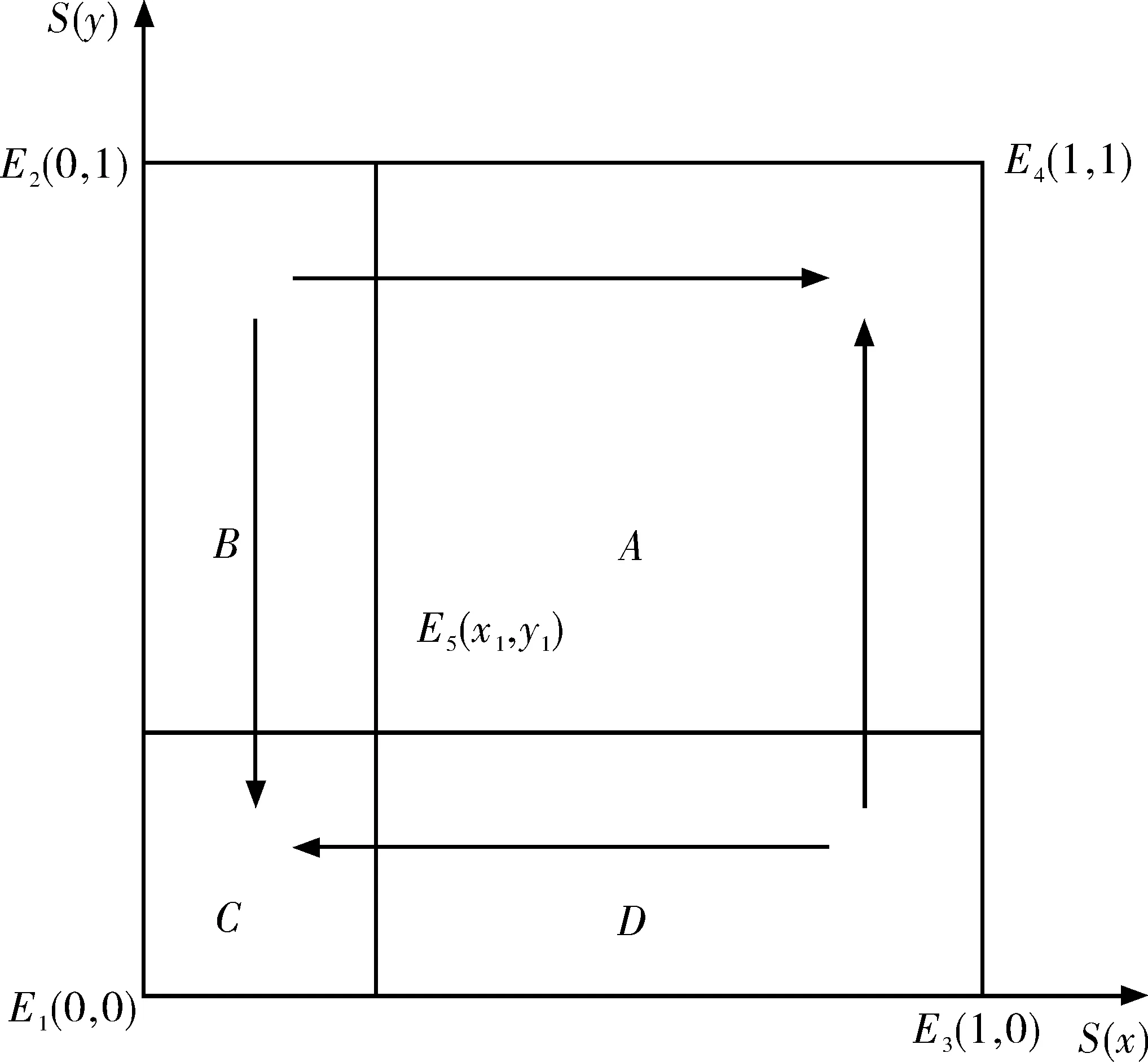
3 影响演化路径的因素和仿真分析
3.1 影响演化路径因素
3.2 仿真分析

4 结 语
