整合到意义教学中，理解余数大小“不再多余”

江西南城县第一小学（344700）

“有余数的除法”安排在北师大版教材二年级下册，例1是关于表内除法的竖式，例2是揭示带余除法的意义，例3是总结归纳余数小于除数的定律。教学例2和例3后均安排了“做一做”，此部分内容被划分为一课时。细细分析，这样划分课时尚欠妥当。因为学生在列竖式时就会碰到余数大于除数的问题，如果没有学习例3，说理就会不充分。如果将余数规律前置，又会造成落实不到位。那么，是否可以将余数小于除数的规律的教学放到竖式教学之前？本文将对此做深入的探讨。

—、余数难学的缘由

学生对带余除法的横式格式并不陌生，被除数、除数、商的意义都未变，可直接从整除除法算式中迁移过来，而余数是新生事物，于是教学重点落在余数的意义上。余数是一个新概念，有着特定的内涵和外延，概念的内涵是本质特性。对于三年级的小学生来说，余数的内涵可表征为平均分后剩下的零头；外延是指概念所指代的所有元素。如，若除数为5，余数则有可能为1、2、3、4；若除数为7，余数则有可能为1、2、3、4、5、6……简言之，余数要比除数小。

除法竖式是全新的算式样态，易受加减竖式的负面影响。能否用演绎推理法，重新解读带余除法的竖式呢？

（1）除法竖式的形式为何呈现阶梯式？如果没有余数存在，除法竖式就和加减乘法一样。除法竖式的阶梯形，完全是为了处理余数的循环运算，它不但展示了商数和除数的积，又设计出空白处书写余数，更能体现余数的地位和价值。

（2）如果先学表内的整除除法竖式，学生就只是根据乘法口诀一步到位得出商数，“商×除数”求积这一步的思考过程容易被架空。先学带余除法，则可避免这种情况。

（3）余数比除数小的根本原因需要追溯到余数的意义。教材在阐述此规律时，只是单一地举出除数都是5的例子，就马上得出结论，例证不够丰富，说服力不够强，对于“除数是4、6、9时，余数可能是哪些数？”这个问题，有些学生就会拿余数和商数进行比较，误认为余数比商小就行。

教材中三个例题所涉及的三个知识点不是孤立的，应该联系起来。横式和竖式都能展现带余除法的意义，学习余数大小限制的规律应该安排在充分认知带余除法意义之后。

从课的容量来考虑，应跳过竖式学习，直接进入带余除法的内容。

基于以上理论，我做了教学改进：重点落在除法意义和竖式书写上，将余数大小的规律融入情境，整合到意义的理解上。

二、整合资源，在意义中体现大小差异

习题1：光头强在林场里砍伐了15棵樟树，每辆卡车装载5棵，可以装载几卡车？你是怎么想的？15、5和3分别属于算式中的什么数？（复习除法算式和各要素意义）

习题2：光头强后来又砍伐了19棵松树，每辆卡车装载5棵，可以装载几辆卡车？圈一圈，并用算式表示。（用圈画的形式，将生活经验调用到数学算术上）

思考：为什么不把最后4棵松树也圈一圈？最后4棵如何反映到算式里？学生的方法：5×3+4=19，19÷ 5=3……4，等等。师（引导学生着重研究除法）：这个除法算式与以前学过的整除除法略有不同。

【评析：第一次对比：有余数和没有余数。讨论如何表示和处置剩下的4棵松树，一是为了揭示余数的意义；二是得出如何在算式中演示。通过讨论，突破原有的认知局限，突出余数的内涵：平均分剩下的不够分一份的零头，必然要比一整份的数目小。】

练习：19棵松树，每车装载3棵，可以装载几卡车？还剩下几棵树？请先圈画再列式。

师：说说圈画的结果。刚才最后剩下4棵不够一份，为什么现在4棵又能分了？

【评析：这是第二次对比。通过对比剩下的棵数，引发学生的好奇心，从而得出“余数够不够分一份，要看具体除数是多少，也就是一份的数额”。】

师：余数是怎么产生的？

【评析：改变除数，集中讨论“余下4棵”能不能再圈的问题，在对比中突出余数和除数的关系，使学生知晓余数的产生过程。】

师（出示图1）：带余除法也有竖式。你能结合圈画过程说说其中每个数的意义吗？

【评析：为了在算法中渗透算理，先让学生自行探讨竖式的意义，结合圈画理解每个数的意义，从而达到理解余数的目的。】

图1

三、练习巩固，内化余数的大小定律

习题1：先圈画，再写出横式和竖式。

（1）12块巧克力，每人分5块，可以分给几个人？还剩几块？

（2）12块巧克力，每人分4块，可以分给几个人？

师（重点分析第（2）题）：分配之后有剩余吗？竖式中两次出现数字12，两个12意义一样吗？余数为什么是0？这其实就代表整除。

【评析：第（1）题是为巩固带余除法的运算，第（2）题则是通过带余除法揭示整除的本质。这样，把整除整合到带余除法里，重点辨析竖式中2个12的含义和区别，以及余数是0的特殊情形，就能说明整除是一类特殊的带余除法的事实。】

习题2：请你猜测图中的小动物各代表数字几。

师（重点解说第（2）题）：这题有多种填数方案。我把大家的方案展示如下，请指出错误的竖式。

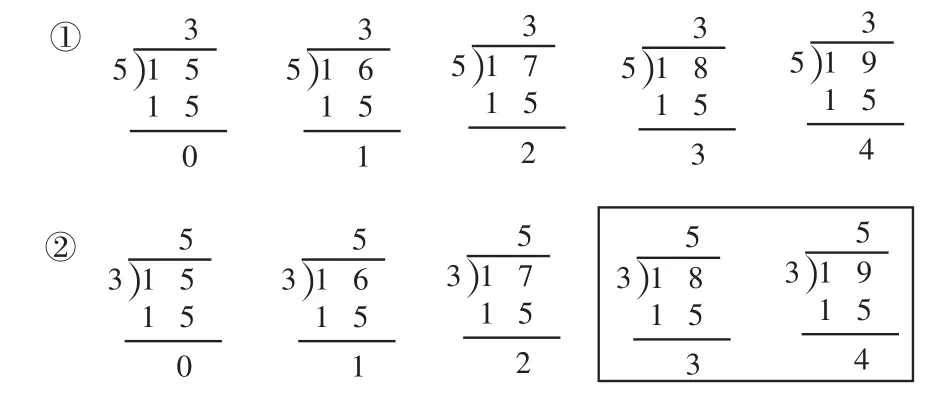
师：观察框内的两个竖式，请你通过画图的方式说说为什么错了。

【评析：把竖式转换成图形，并指出错误，既是梳理和总结知识，又是对新知的应用，为总结规律提供了丰富的实证，诠释了余数与除数的关系。】

综上所述，要想在有限的时间内用科学合理的课时量完成带余除法的教学，并让学生深刻理解余数要比除数小的原理，教师必须调整教学顺序，整合教学资源，这样才能取得事半功倍的效果。