在多维活动中提升学生的数学核心素养
——“三角形三边关系”的教学片段及思考
2018-11-15江苏南京市玄武区教师发展中心210000
江苏南京市玄武区教师发展中心(210000)
《义务教育数学课程标准》(2011年版)在实施建议中指出:“数学教学应根据具体的教学内容,注意使学生在获得间接经验的同时也能够有机会获得直接经验……引导学生通过实践、思考、探索、交流等,获得数学的基础知识、基本技能、基本思想、基本活动经验,促使学生主动地、富有个性地学习,不断提高发现问题和提出问题的能力、分析问题和解决问题的能力。”基于这样的建议,教师在课堂教学中要尽量引领学生经历知识产生和发展的过程,让学生通过动手操作、观察对比、数据分析、抽象推理等多维活动,更好地理解知识,提升数学核心素养。下面以苏教版教材四年级下册“三角形三边关系”的教学为例进行论述。
【片段一】动手操作,合作探究
师:老师今天给每位同学带来了一张16厘米长的胶带,请大家把它剪成三段。为了便于研究,只剪成整厘米数,然后围一围,看剪成的这三条胶带能不能围成一个三角形。
学生四人小组合作操作:量—剪—围—记录。
我的探究:把16厘米长的胶带剪成三段,围一围,把三条边的长度以及能不能围成三角形的情况记录在表格中。
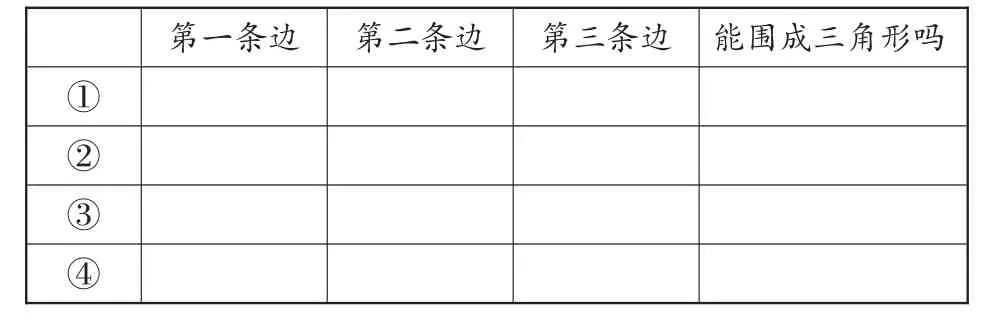
第一条边 第二条边 第三条边 能围成三角形吗①②③④
【片段二】分享交流,发现规律
(学生一一介绍围成的或围不成的具体数据,并展示围的过程;教师板书相关数据)
重点研究两边之和等于第三边的情况:
(1)若学生能围成。师:大家都同意吗?有没有和他的情况类似的数据?
师(出示课件):我们借助课件来看一看。
(2)若学生围不成。师:你们同意他的想法吗?(学生表示质疑)
师:大家的要求可真严格呀!不过,学习数学就需要有这样认真的态度。把上面的两条边再向下压一压,能不能围成三角形呢?
师:上面两条线段的长度之和是8厘米,下面一条线段也是8厘米,能围成吗?想一想,再用手比画。学数学就要用数据去考虑问题,不只是用眼睛看,还要用心想。老师也做了一个和这个同学一样的三角形。大家看一看围成三角形了吗?
师:真的围成了吗?我们放大看一下。
生1:没有围成,中间还有一点缝。差一点也不行。
师:想象一下,当这两个点真正相连的时候会出现什么情况?
生2:上面的线段会和下面的线段重合。
师:看一看是不是真的这样?(课件演示)
师:这是一个小组的数据,其他小组有不同的吗?
【片段三】观察思考,总结规律
师:都是由16厘米长的胶带剪成三段,只是长短不同,为什么有的能围成,有的围不成呢?结合刚才围三角形的过程,仔细观察数据,你有什么发现?
学生总结,教师板书:
两边之和大于第三边;
任意两边之和大于第三边;
较短两条边之和大于第三边;
两边之和小于第三边不能围成三角形;
两边之和等于第三边不能围成三角形。
交流:先解决“小于”的和“等于”的。
师:你能结合黑板上的数据说一说你的想法吗?(移—说—板书式子)
师:对于这几个发现,你同意哪一个呢?(学生自由辩论)
师:刚才大家通过动手围三角形,发现了三角形任意两条边的和大于第三边。你对这句话还有什么疑问吗?是不是有一个词特别关键?为什么要加上“任意”呢?拿掉不行吗?
【片段四】抽象概括,建立模型
师:老师这里还有三条线段,它们的长度分别是a、b、c,不知道谁长谁短,那当它们具有什么关系时,就能围成三角形?(结合学生回答板书)
a+b>cb+c>aa+c>b
师:只有同时满足这三个条件,才能围成三角形。
这节课是图形与几何领域中关于三角形认识的内容之一,在学习这个内容之前,学生已经认识了三角形,因此这节课的教学目标是通过实验活动,让学生理解“三角形任意两边的和大于第三边”,并能用它解决一些简单的实际问题。
这节课的教学,教师能够充分尊重和用好教材,让学生始终处于课堂的“中央”,给予学生合理的支持,在实际的操作、丰富的想象、交流和辨析中,让数学学习自然而灵动地发生。
一、基于操作的感受和体验
苏霍姆林斯基曾说过:“儿童的智慧在他的手指尖上。”通过动手操作可以把抽象的数学知识具体化和形象化。片段一中,教师为学生提供16厘米长的胶带,并组织学生带着任务动手操作:把胶带剪成整厘米的三段,看能否围成三角形。学生在操作的过程中,不断地思考“我剪的能围成三角形吗?”剪下来后围一围,能围成的,记录数据;围不成的,主动寻找原因。学生在围的过程中发现,以最长的边为底边,如果两条较短边在不断靠近的过程中不会相交或与最长边重合时才相交,这样肯定围不成三角形。这种操作经验为后续理解规律提供了强有力的支持,为后续分析数据和总结规律打下了基础。这也让数学学习不再是单一枯燥的模仿记忆,而变成了一种不断探索、发现和提升的过程,让学习充满了张力和个性。
二、基于数据的推理和发现
学生通过动手操作得出九组围成或围不成三角形的具体数据,教师组织学生对数据进行深入分析:先按围成和围不成三角形对数据进行分类,再对同类和不同类的数据进行对比、观察,形成观点,然后再全班汇报交流,大家相互质疑,不断完善。在这个过程中,学生的批判性思维在发展,语言表达能力在提升,合情推理能力在生长。得出结论后,学生又用数据去证明自己的发现是对的,这时演绎推理与分类思想又悄然出现了。
三、基于直观的想象和理解
毋庸置疑,操作活动是学生积累基本活动经验的一个重要方式,也是学生发展空间观念的一个必要抓手,但学生空间观念的发展,必然要经历从直观到逐步抽象的过程。在本节课中,对于“任意两边之和等于第三边是不是能围成三角形”,是学生在操作时极易发生争议的,因为剪的损耗、围的误差都会影响操作的结果,会让学生感觉到是可以围成三角形的。为了突破这一教学难点,教师充分利用了课件演示、动手比画、直观想象等方式。这样的处理方式,不但巧妙地突破了教学的难点,也促进了学生空间观念的发展。
综上,只有让学生在不断地操作、观察、思考、想象、分析中,探索出三角形三边的关系,发现其内在的规律,才能在发展学生空间观念的过程中,培养学生独立思考、合作交流的能力,提升学生的数学核心素养。
