基于博弈理论的大用户直购电模式项目研究

张琪 刘琰 王宁宁

(山东电力工程咨询院有限公司，山东 济南 250014)

0 引言

随着中国特色社会主义市场经济的发展，在政府监管、市场干预共同作用下的电力市场逐步完善，正朝着更为健康化的方向发展。在这样的社会发展潮流之下，我国电力市场推行的大用户直购电交易模式作用显著。首先，通过电力市场中买卖双方的直接博弈，实现了对电力大用户电价的定价合理化；其次，随着发电市场的市场化进程加快，打破了发电的垄断性，使得社会资本更多地参与其中，降低了生产成本，提高了发电效率和效益；最后，在推行大用户直购电模式的过程中加强了政府的监管力度，保障了市场的健康有序发展[1]。

在实际电力项目交易市场中，项目双方的信息往往是不完全对称的，而且买卖双方的实力也是不对等的，项目双方的均衡点可能不是卖方的供应曲线和买方的需求曲线的交叉点处[2]。因此，在项目研究过程中需要建立买卖双方的动态谈判博弈模型，在这个模型当中主要要分析项目双方在信息不完全对称、实力不对等情况下双方的博弈结果。

1 直购电谈判动态博弈模型的建立

在直购电项目研究当中，假设项目双方通过合约交易的模式进行电力交易。假设未来不确定的某个时间段内该大用户的用电量总和为Dj，而在该对应的时间段内卖方实际参与的双方交易当中的电量总和为Qi。电价参照的是现货交易模式下的电价，用PS表示。在大用户直购电合同签订之前，项目买卖双方虽然没有就电价进行谈判，但当时双方均会有自身所期望的最理想电价，分别用Psg.i和Psb.j表示卖方和买方所期望的理想电价。这两个期望的理想电价不是共享的。这两个期望值与实际电价Ps之间会存在一个或正或负的差值，这个差值用δ2表示。为方便在研究中更为简洁，假设δ2是买卖双方在博弈过程中的共同认知。最终买卖双方通过博弈所达成的最终合同电价用Pc.ij表示。

在这个项目的动态博弈模型中假设Qi=Dj，并且双方对风险的厌恶程度为wg.i=wb.j，在这种情况下，建立项目买卖双方信息不对称、实力不对等情况的动态博弈模型。

买卖双方在谈判过程中，会在一点上达成共识，即尽可能地降低自身所承担的风险，并不断试探对方的需求和供应情况。在这种动态博弈条件下，Psg.i和Psb.j是不能共享的私密信息[3]。项目双方均会估计Psg.i和Psb.j服从在[a,b]上的均匀分布、双方的供给和需求状况以及其他函数中的参数，这些均是双方在不断的博弈过程中逐渐达成的。

如果买方不接受，则项目双方的博弈继续进行第2阶段，直到第n个阶段。见图1。

图1 发电公司i与大用户j的博弈流程图

项目双方的博弈就像这样不断重复进行，直到双方达成一致。这样的博弈过程可以有n个阶段。当n为奇数时，是卖方提出策略，由买方决定是否同意；当n为偶数时，由买方提出策略，由卖方决定是否同意。

2 直购电谈判博弈模型的求解

为求解直购电谈判博弈模型，本研究选择的方法是逆向归纳法。

在项目双方的动态博弈过程中，如果第1阶段双方未能达成共识，那么对于卖方而言进入第2阶段会存在较大的潜在风险，因为在第2阶段买方肯定会降低价格，如果同意，会造成收益降低；如果不同意，还会进入下一轮的博弈当中。因此，对于卖方而言，只要满足

那么，卖方一定会接受此时的电价。

提出电量电价。因此买方在第2阶段所能采取的最优策略为

(1)

式中，Pga.i代表的是卖方所能够接收买方提议的概率；Pgr.i代表的是卖方拒绝接收买方提议的概率。

由此有

Pga.i=1；Pgr.j=0

求解式(1)，得到

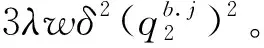
因此，在第1阶段的项目双方谈判过程中，能够使买方接受卖方所提出的电价电量的前提是买方能够在第1阶段就获得大于第2阶段的谈判效益。即

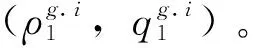
(2)

因此，买方在第1阶段谈判当中的最优策略为

式中，Pba.j为在第1阶段中大用户接受的概率;Pra.j为在第1阶段中大用户拒绝，但在第2阶段中，发电公司接受的概率。即

Pra.j=Pbr.j×Pga.j

(5)

将式(2)、式(4)、式(5)代入式(3)中，得到

由上，得到了单个大用户单个发电公司情况下的序贯博弈的均衡解。

3 具有合约交易的现货交易电价均衡模型

本研究假设项目双方经过博弈之后所签订的大用户直购电合同的电量为xiQi，电价为Pc.ij(i=1,2,…,n;j=1,2,…，m)。

在电力市场的交易模式中，现货交易的模式是卖方不断追求自身利益最大化，因此在这种交易模式之下，卖方的目标函数可以表述为

maxπi=Ps(qi-di)+hidi-Costi(qi)

式中，πi代表的是卖方的利润值。

卖方从基于利润最大化的角度出发，所生产的最终电量可以表示为

将上式中N个数值进行行汇总求和运算。可以得到卖方在利润最大化情况下的最优电量。可以表示为

求解以上方程式，可以分别得到当电力市场处于均衡状态之时的电量和电价。其中电量和电价可以用公式表示为

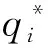
从以上公式可以看出，电量和电价成反比的状态存在，也就是说当项目双方通过签订大用户直购电合同，且合同中明确电价时有利于市场上出清电价的下调。

4 合约与现货交易电价均衡模型的耦合过程

在项目双方的博弈过程中，如果买卖双方的信息是完全对称的，而且买卖双方实力对等，那么在博弈过程中，买卖双方所达成的博弈均衡点应该为卖方的供应曲线和买方的需求曲线的交叉点处。但是，如果买卖双方的信息不完全对称，而且买卖双方的实力不对等，那么买卖双方的均衡点可能不是卖方的供应曲线和买方的需求曲线的交叉点处。买卖双方通过不断的博弈过程实现均衡。本研究具体的建模和分析过程可以总结为：

步骤一：分析电力市场中如果仅仅存在现货交易这一种交易方式时，项目双方达到均衡时的电量和电价。

步骤二：在分析现货交易的基础上，分析大用户直购电这种合约交易模式中，项目双方达到均衡时的电量和电价。

步骤三：在分析大用户直购电这种合约交易模式的基础上，将此时所得到的电量和电价融合到现货交易模式中，求解在大用户直购电模式下，现货交易达到相对均衡时的电量和电价。

步骤四：不断重复步骤二和步骤三，直到两种交易模式均达到均衡状态。

5 结语

通过构建博弈模型可以看出，市场的透明度越高，电力市场中的交易者对电力市场交易信息及变化趋势越了解，越会使得出清电价下降，总交易电量上升，总社会福利提高。