驾驶经验对稳定跟车行为的影响

朱兴林，王 媚

(新疆农业大学 交通与物流工程学院，新疆维吾尔自治区 乌鲁木齐 830052)

跟车过程中驾驶员的驾驶经验是影响交通行为的重要原因。人-车-路-环境四要素组成的道路交通系统中，人(尤其是驾驶员)作为处理交通信息的判断者和决策者，其反应能力影响着整个系统的运行，是道路交通系统中最重要和最活跃的因素[1]，反应时间是衡量驾驶经验的主要指标。近年来，国内外学者对驾驶员反应能力的研究做了很多拓展性工作，Ossen等[2]利用反应时间和敏感度量化了驾驶员的反应能力，分析了个体驾驶员之间的跟车行为差异；王福建等[3]基于实际的驾驶行为特性，将驾驶员的驾驶状态分为强跟驰、弱跟驰和自由流三种状态，建立能够描述这三种状态的车头时距三元混合分布模型；Piao等[4]根据实测数据发现跟车距离随速度的增加而增加，且在高速路段行驶时的跟车距离相较于低速时存在较大的波动；张智勇等[5]利用基于GPS的实时动态车辆跟驰数据采集方法，较好地解决了跟车状态下驾驶员行为和车辆运行特征的时间序列实测数据采集问题；李广玉[6]，王亚培[7]等利用计算机仿真技术，结合模糊控制规则给出高速公路上车辆跟驰行为的一种仿真。袁伟等[8]通过实测高速公路上驾驶员的跟车数据，探讨了稳速跟车阶段驾驶员的期望跟车间距与跟车速度之间的关系；菅美英等[9]基于驾驶模拟试验数据，分析老年驾驶员的跟驰行为特征，并深入研究驾驶员跟驰行为的影响因素。

以上跟车行为的研究侧重于根据模型进行理论分析，对驾驶经验差异考虑较少。鉴于此，本文利用车载激光雷达设备，以不同经验的驾驶员为试验对象，在实际交通流中获得有无经验驾驶员稳定状态下的行车特征，从而给研究不同经验驾驶员的跟车行为提供可靠的试验数据。

1 试验设计

1.1 试验设备

Hi-Drive10跟车驾驶行为分析系统由北京奥泽尔科技发展有限公司研制，不仅能够采集跟车状态下的各类数据，还可用于交通流量计算、微观交通仿真、道路通行能力分析和交通安全影响评价等交通工程学的研究。Hi-Drive10跟车驾驶行为分析系统由数据分析软件、硬件设备及辅助装置三部分组成。

1.2 试验对象

本试验总共招募非职业性且持有中华人民共和国C1驾照的驾驶员56名，身体健康，无明显影响交通行为的身体特征，其从事的职业主要有学生、教师、职员、个体户及自由职业者，年龄20岁～55岁，其中女性驾驶员16名，男性驾驶员40名。因驾驶经验无法用驾龄进行科学地衡量，为突出驾驶经验对反应时间的影响，选择驾驶里程数作为分组标准，将试验对象分为无经验驾驶员和有经验驾驶员两组，其中无经验驾驶员的驾驶里程在10万km以下(驾龄小于或等于5年)，有经验驾驶员的行驶里程在20万km以上(驾龄大于或等于10年)[10]，无经验驾驶员和有经验驾驶员各28名。受试驾驶员基本情况如表1所示。

1.3 试验道路

选取乌鲁木齐市河滩快速路新医路入口到米东区出口作为试验路段，全长约15 km，双向6车道，小客车限速100 km/h。该路段路面情况良好，以小汽车为主，车辆跟车状态稳定，该路段能在相对稳定的环境下突出驾驶员的驾驶行为特点。

表1 受试驾驶员基本情况

1.4 试验车辆

试验假定影响跟车行为的主要因素是由驾驶经验决定，车辆的选择上尽量为驾驶员创造相似的行驶环境，排除车辆因素对驾驶员跟车行为的影响，是本次试验的首要条件，故试验车辆选择家用小型汽车。

1.5 试验过程

试验从2016年4月开始至2016年6月结束，每次试验前期会寻找符合试验条件的驾驶人员、试验车辆及其他准备事项，除去为了测试设备是否正常运行的2次实地试验，可使用的试验数据总共有先后7次。另外，试验均选择天气及道路交通条件良好的白天进行。

2 稳定跟车状态下驾驶经验对跟车距离的影响

稳定跟车状态是指车辆在进行跟车行为时，在一定的时间内保持恒定的行驶状态，是交通流中最常见、占据时间比例最大的一种交通状态，影响到交通流的整体运行状况，对交通流的影响至关重要[11]。判断稳定跟车状态的方法一般有两种：一种是定义速度差Δv=0时为稳定跟车状态。另一种定义方法以加速度为判断标准。Ozaki[12]定义车辆加/减速度在±0.5 m/s2内的行驶状态为稳定跟车状态，而Sultan[13]确定的加/减速标准为±0.6 m/s2。张智勇[14]根据试验采集的数据利用聚类分析法将跟车过程分为加速启动、稳定跟车和减速停车三个部分，结果表明加/减速度在[-0.677 m/s2，0.533 m/s2]为稳定跟车状态，这一结果与Ozaki和Sultan的结果比较接近。考虑到驾驶员对速度的判断误差和驾驶操作的不稳定性，本文将加/减速度在[0.6 m/s2，-0.6 m/s2]时的跟车行为定义为稳定跟车状态，选取符合加/减速度特征的跟车数据，如图1所示。

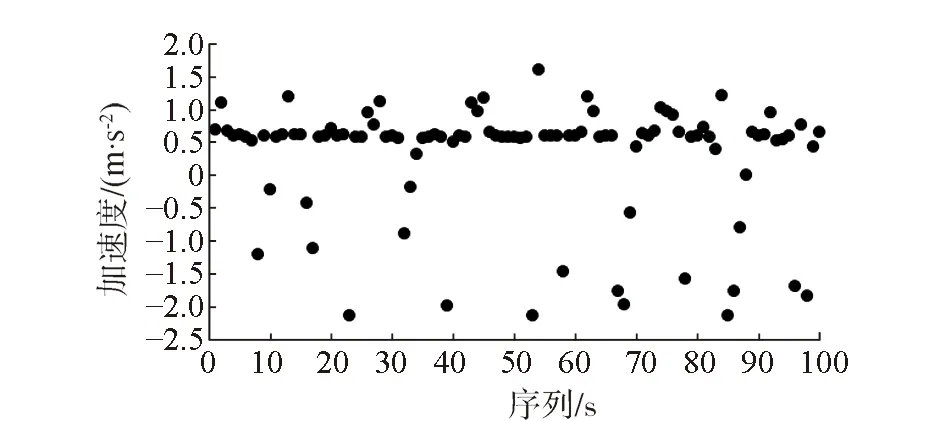
图1 符合稳定跟车条件的加速度

2.1 跟车距离统计分析

由于试验道路在乌鲁木齐市河滩快速路进行，小型汽车限速100 km/h，两类驾驶员在不同跟车速度下跟车距离反应的规律大致相同，故选取跟车速度为80 km/h的跟车距离作为试验分析数据，跟车距离统计描述及箱形图如表2、图2所示。

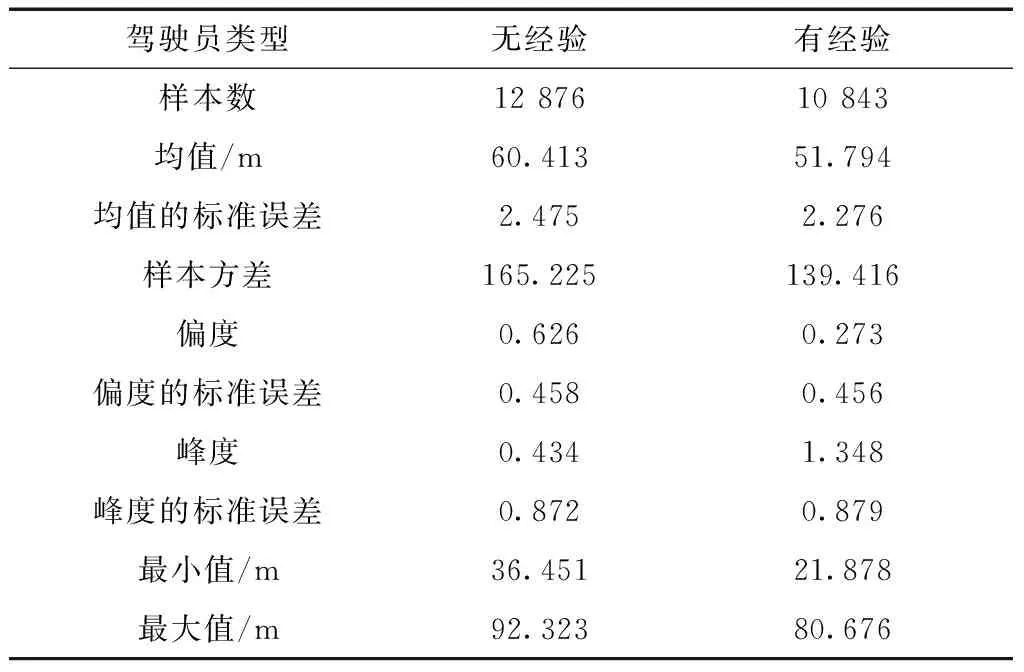
表2 稳定跟车状态下跟车距离统计表

由表2可知，无经验驾驶员跟车距离的均值最大最小值均比有经验驾驶员要高。由图2跟车距离箱形图来看，无经验驾驶员的跟车距离普遍比有经验驾驶员高，这与无经验驾驶员驾驶技能不熟练、心理素质差等因素有关，符合驾驶员个人特性。

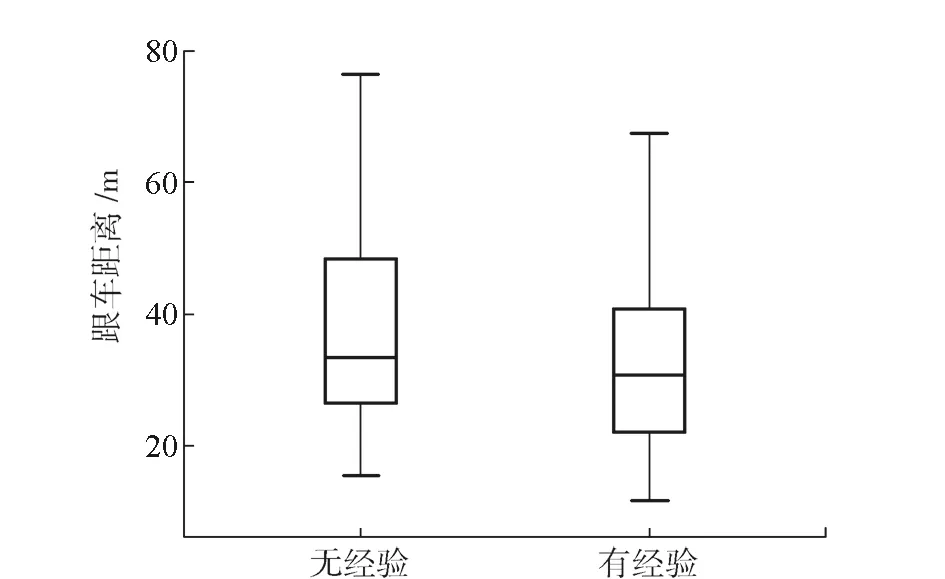
图2 稳定跟车状态下跟车距离箱形图

2.2 相关性分析

由于驾驶里程是衡量驾驶经验的重要指标，驾驶里程越长相应的驾驶经验也越丰富，为定性分析稳定跟车状态下驾驶经验对跟车距离的影响，将每位驾驶员的跟车距离均值列出，并与累计行驶里程进行显著性检验，检验结果如表3所示。

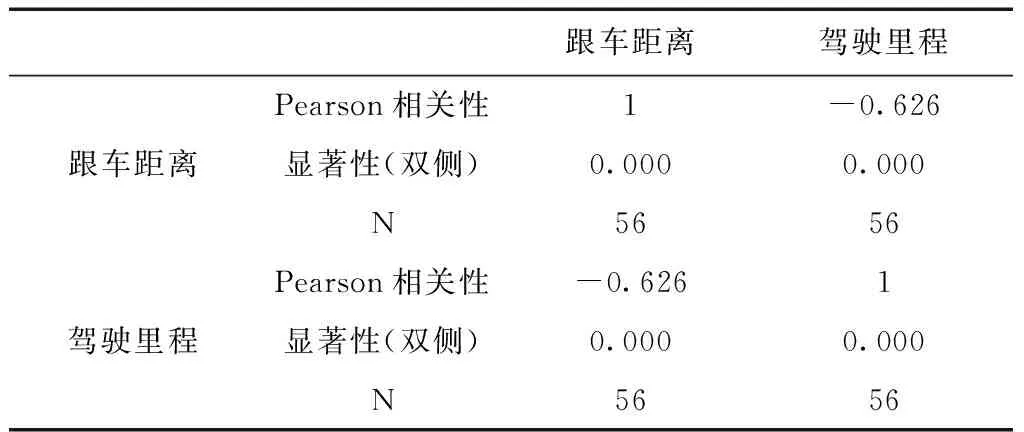
表3 驾驶里程与跟车距离相关性分析

由表3相关性分析结果可知：在置信度(双侧)为0.01时，驾驶里程与跟车距离的相关性非常显著，相关系数显著不为0(Pr=0.00<0.05，且相关系数-0.626为负值，说明驾驶里程与跟车距离存在负相关关系，即驾驶里程越长，跟车距离越小，驾驶里程越短，跟车距离越大。

2.3 跟车距离分布函数

考虑到样本中少量噪声点对检验结果产生影响，本文采用随机抽样的方法。每次随机抽取100个样本，重复抽取100次，并对每次抽取的样本数据进行拟合和检验，从而得到稳定跟车状态下跟车距离分布函数的参数拟合如表4所示。

由表4可知，拟合得到的Gamma分布函数的参数变异系数范围为[0.1，0.3]，而对数正态分布函数的参数变异系数范围为[0.03，0.09]，对数正态分布函数的参数变异系数在10-2等级，远远低于Gamma分布函数，故对数正态分布函数更能符合稳定跟车状态下跟车距离的分布规律。稳定跟车状态下跟车距离的频数分布图如图3所示。

表4 稳定跟车状态下跟车距离分布函数拟合

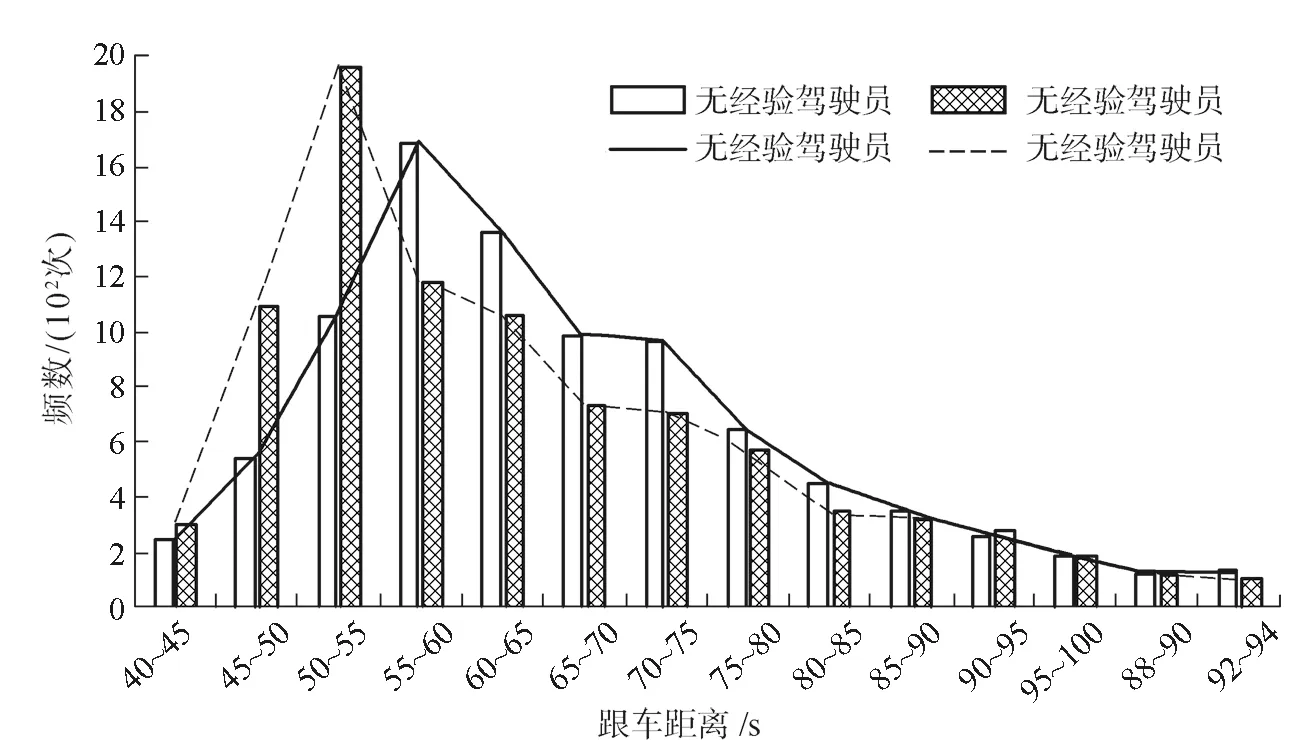
图3 稳定跟车状态下跟车距离频率统计图

由图3可知无经验驾驶员跟车距离主要分布在55～75 m，有经验驾驶员则主要分布在45～65 m，无经验驾驶员频数峰值最高的跟车距离要高于有经验驾驶员。根据随机抽样的方法得知，对数分布函数能很好地反映稳定跟车状态下驾驶员的跟车距离特性，故无经验驾驶员和有经验驾驶员分别服从lnN(2.985，0.828)和lnN(2.874，0.954)的对数正态分布，密度函数如式1、式2所示。

(1)

(2)

综合以上分析可知驾驶经验对跟车距离有以下影响作用：稳定跟车状态下，无经验驾驶员的跟车距离普遍比有经验驾驶员高；驾驶里程与跟车距离有着明显的相关性，且相关系数为负值，说明驾驶里程越短跟车距离越大，驾驶里程越长跟车距离越小。

3 稳定跟车状态下驾驶经验对车头时距的影响

3.1 车头时距统计分析

稳定跟车状态下车头时距的定义为跟车距离与跟随车(试验车)速度的比值[15]，如式3所示。在稳定的交通流中，驾驶员完成相关反应和操作是以车头时距为控制要素的，而反应能力和操作能力与驾驶员的个人经验密切相关，故研究驾驶经验对车头时距的影响，能更好地理解跟车过程中驾驶员个人特性与跟车行为的关联关系。

(3)

式中：ht为t时刻驾驶员的车头时距；Δx(t)为t时刻前导车与跟随车相对距离；v(n+1)(t)为t时刻跟随车的瞬时速度。

由于速度过低时影响驾驶员跟车行为的因素增多，以此为衡量驾驶员反应能力和操作能力存在较大误差，而速度过高车头时距过小，跟车行为特征减弱，根据车头时距的定义，选取跟车速度为20 km/h～80 km/h的车头时距作为试验分析数据，车头时距统计描述及箱形图如表5、图4所示。

由表5可知，无经验驾驶员车头时距的均值及最大值比有经验驾驶员要高，最小值相同。由图4可看出，无经验驾驶员的车头时距普遍比有经验驾驶员高，说明无经验驾驶员为了自身行车安全会对前导车的排斥性更强，且相对有经验驾驶员会保持较大车头时距，符合驾驶员个人特性。

3.2 相关性分析

同样，为了进一步分析稳定跟车状态下驾驶经验对车头时距的影响，将累计行驶里程与车头时距进行显著性检验，检验结果如表6所示。

表5 稳定跟车状态下车头时距统计描述

图4 稳定跟车状态下车头时距图

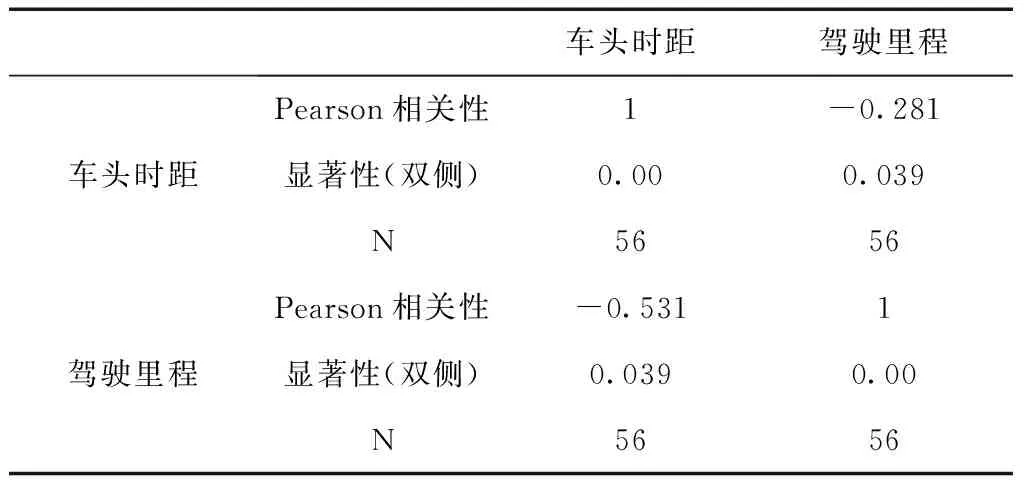
车头时距驾驶里程车头时距Pearson相关性1-0.281显著性(双侧)0.000.039N5656驾驶里程Pearson相关性-0.5311显著性(双侧)0.0390.00N5656

由表6可知，置信度(双侧)为0.01时，驾驶里程与车头时距的相关性较显著，相关系数显著不为0(Pr=0.039<0.05)，且相关系数为负值-0.281，说明驾驶里程与车头时距存在负相关关系，即驾驶里程越长，车头时距越小，驾驶里程越短，车头时距越大。

3.3 车头时距分布函数

同样对所有车头时距数据进行简单随机抽样，每次随机抽取100个样本，重复抽取100次，对每次抽取的样本数据进行拟合和检验，将所有抽取到的跟车距离的平均值作为拟合参数，得到稳定跟车状态下车头时距频率分布如图5所示。

图5 稳定跟车状态下车头时距频率统计图

由图5可知无经验驾驶员的车头时距集中在5.6 s～6.2 s，有经验驾驶员则在5.4 s～6.0 s。图5显示的频率曲线分布规律类似于正态分布，并对该分布进行检验。利用矩估计法计算无经验驾驶员的期望值μ=6.062，标准差σ=0.349；有经验驾驶员的期望值μ=5.900，标准差σ=0.250。对拟合后的模型进行假设检验：H0：假设车头时距服从参数为[μ，σ]的正态分布；H1：假设不服从参数为[μ，σ]的正态分布。分别进行单样本的K-S检验得无经验驾驶员检验值车头时距p=0.585，有经验驾驶员反应时间p=0.328，故两类驾驶员反应时间均接受原假设H0(0.05的显著水平下)。

为了进一步验证H0的假设，通过Q～Q图进行检验，如图6所示。

综合K-S检验的值和图6可知，拟合的正态分布模型与实测数据有较好的匹配度，故无经验驾驶员和有经验驾驶员的车头时距分别服从N(6.092，0.349)和N(5.900，0.250)的正态分布，密度函数表达式如式4、式5所示。

(4)

(5)

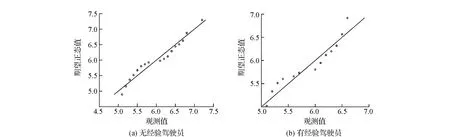
图6 车头时距Q～Q图分布检验

综合以上分析可知驾驶经验对车头时距有以下影响：稳定跟车状态下，无经验驾驶员的车头时距普遍比有经验驾驶员高；驾驶里程与车头时距有着明显的相关性，且相关系数为负值，说明驾驶里程越短车头时距越大，驾驶里程越长时间将越小。

4 结束语

本文在特定的交通环境下，利用车载激光雷达设备分析了稳定跟车状态下有无经验驾驶员跟车行为特性，研究结果表明稳定跟车状态下，无经验驾驶员的跟车距离普遍比有经验驾驶员高，驾驶员的累计驾驶里程与跟车距离有显著的相关性，相关系数为负值，说明随着累计驾驶里程的增加跟车距离随之减小；无经验驾驶员的车头时距也普遍比有经验驾驶员高，驾驶员的累计驾驶里程与车头时距有显著的相关性，相关系数亦为负值，说明随着累计驾驶里程的增加车头时距随之减小。探究驾驶经验对稳定跟车行为影响可了解不同驾驶员的跟车行为差异，从而能有针对性地对无经验驾驶员进行反应能力训练，提高其在实际道路上的应急水平，进而提高行车安全性。