基于改进灰色马尔科夫模型的地铁客流预测

潘 杰，马超群

(长安大学 公路学院，陕西 西安 710064)

随着城市轨道交通实时交通信息系统的日益完善，管理者需要掌握未来短时间内客流量的变化趋势，以制定和实施运营管理计划，这不仅可以使交通管理逐步走向智能化、动态化和信息化，还能提高运营效率，同时为出行者提供高效方便的服务。

文献[1]提出了基于Kalman滤波的短时地铁换乘客流预测方法，得到平日早高峰客流预测结果评价指标均优于节假日的预测结果，但存在对突变点预测不够准确。文献[2]选用SARIMA模型对北京市地铁进站客流量预测进行短时预测，预测结果基本能够满足对客流掌握的需求，但该模型对于特殊节假日的预测效果甚微；文献[3]将K近邻非参数回归应用于轨道交通客流量预测中，发现K近邻非参数回归比其他模型的预测精度更高、对突发客流的处理能力更强。文献[4]将神经网络和支持向量机两种方法融合在一起，得到了组合预测模型；文献[5]则在前人研究的基础上，建立了基于客流时序特征的神经网络模型。

传统预测法和灰色系统理论都可以独立完成一定时期内地铁客流量大体趋势的预测。但由于地铁客流量受到很多未知因素影响，导致数据波动性较大，因此，传统方法和灰色模型在短期预测中预测精度不高。本文考虑到地铁客流量的随机性和连续性，提出一种改进的灰色马尔科夫预测模型。用改进后的模型对西安地铁客流量进行了预测，改进后的灰色马尔科夫模型的准确度和精度都有所提高。

1 改进灰色马尔科夫模型

1.1 无偏灰色GM(1，1)模型[6]

设原始数据序列为严格的指数序列，即

x0(k)=Me-η(k-1)，k=1，2，…，n.

(1)

其一次累加生成序列为

(2)

用传统的GM(1，1)建模方法建模,可得

(3)

Yn=[Meη,Meη,…,Me(n-1)η]T.

(4)

经推导可得

(5)

最终拟合结果为

x′(0)(1)=M.

(6a)

(k=2，3，…，n).

(6b)

根据式(5)，可用传统GM (1，1)模型的参数a,u来表示原始序列的参数η，M

假设指数序列建立的模型为

x0(k)=M′ea′(k-1)，k=1，2，…，n.

(7)

其中，令

式(6a)和式(6b)是一个无偏模型。由此建立无偏GM(1，1)模型，其建模步骤为：

步骤(1)到步骤(3)见本文1.1中传统GM(1，1)模型建立步骤。

步骤(4)：求出无偏GM(1，1)模型的参数

步骤(5)：建立原始数据序列模型

x′(0)(1)=x(0)(1)，

(8a)

x′(0)(k)=M′ea′(k-1)(k=2，3，…，n).

(8b)

与传统GM(1，1)模型相比，无偏GM(1，1)模型基本消除了传统GM(1，1)模型的固有偏差，其应用范围较传统GM(1，1)模型更为广泛。此外，无偏GM(1，1)模型无需进行累减还原，简化了建模步骤，提高了模型的计算速度。

1.2 滑动灰色GM(1，1)模型

考虑数据随着时间变化具有内在的连续性，利用加权平滑思想对原始数据进行处理后，再结合无偏GM(1,1)建模过程建立滑动无偏GM(1,1)模型：

设原始数据序列为

经加权平滑处理得

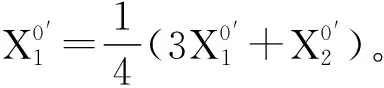
(9)

(10)

对原始数据进行加权处理后，对该组数据利用无偏GM(1,1)模型进行预测，得出的结果即滑动无偏GM(1,1)模型预测结果，该模型预测具有较高的准确性，但对波动数据的适用情况较差。为弥补GM(1,1)模型的不足，引入了马尔科夫模型。

1.3 马尔科夫模型的建立[7-10]

1.3.1 状态划分

地铁客流的变化过程是一个随机呈现上升或下降趋势的非稳定随机过程，地铁客流量的数据序列符合n阶马尔科夫非平稳随机序列。设Y为相应时间序列的取值区域，利用M黄金分割法将Y划分为m个状态，则有H1，H2，…，Hm。

1.3.2 确定系统状态

在有些预测问题中，系统状态是确定的，但有些系统的状态经常需要人为的事先划分来确定系统状态，通常无统一标准。

1.3.3 计算初始概率和一步转移概率矩阵

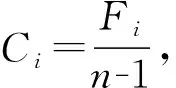
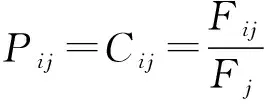
1.3.4 利用P进行系统预测

若时间序列的观测值yt落入状态Hi,Pij=max(Pi1,Pi2,…,Pim)为P的第i行元素，则可预测Yt+1时刻将转移到状态Hj，这是因为转移到状态Hj可能性最大。

1.3.5 利用马尔科夫链的遍历性和平稳分布对系统进行分析。

2 模型应用分析

2.1 地铁客流的灰色马尔科夫模型

本文以2014—2016年西安地铁二号线各站点的AFC数据进行统计分析，可得到二号线每个月的总客流量。将每3个月(一个季度)的客流量进行一次汇总，得到西安地铁客流量的样本数据(见表1)。

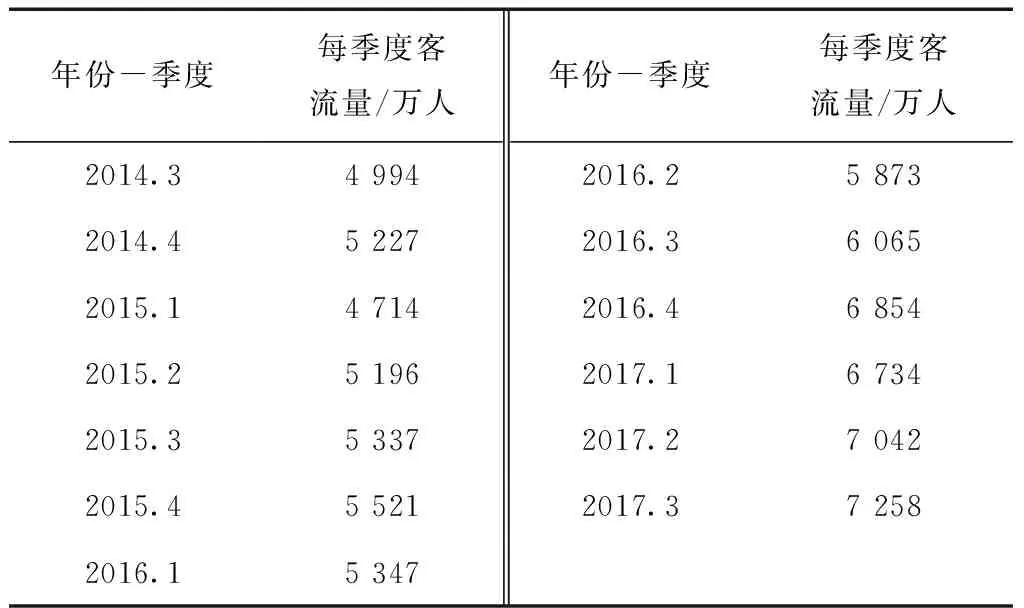
表1 2014.3—2017.3西安地铁客流量实际值

将表1中每个季度的地铁客流总量作为初始数据，对这些数据建立GM(1，1)模型，对2017年前3个季度的客流量进行预测，从而得出2014.3—2017.3西安地铁客流量GM(1，1)模型的预测值(见表2)。

表2 2014.3—2017.3西安地铁客流量GM(1，1)模型的预测值

根据GM(1，1)模型的预测值计算出残差ε(1)(K)和残差的相对值Δ(K)，再把Δ(K)与马尔科夫

模型相结合[11]，由残差的相对值Δ(K)将它们划分为3种状态，分别记为⊕1=(-8%，-2%]，⊕2=(-2%，0]，⊕3=(0，9]。得出2014.3—2016.4的GM(1，1)模型预测值、每年的残差ε(1)(K)、残差的相对值Δ(K)以及各自所处的状态[12]，如表3所示。

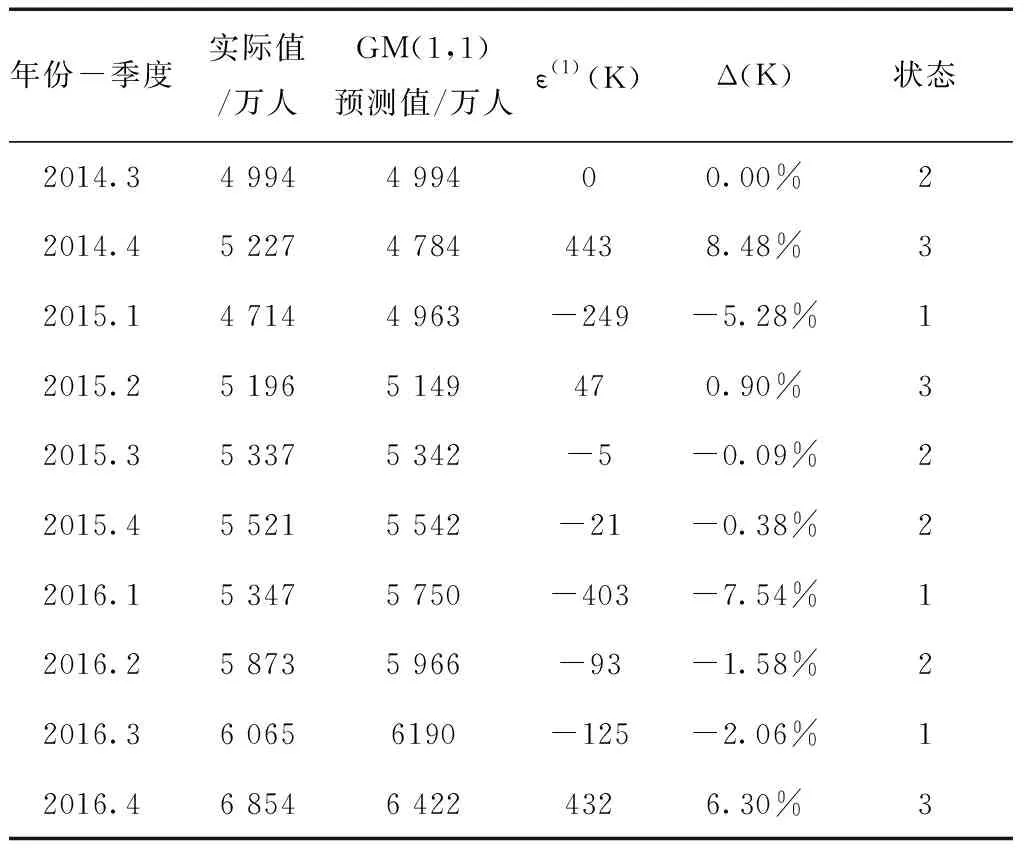
表3 状态分布表

根据表3中的状态划分，对状态转移概率矩阵的分析如下[13-14]:表3中处于状态1的情况共出现了3次，经过一步转移之后的状态分别变为状态3和状态2，由此可得出由状态1经过一步转移过后仍然处于状态3的概率为2/3，转移后到状态2的概率为1/3，依此类推，得到状态转移矩阵为

由于2016年第四季度处于状态3，那么初始向量为V0=(0，0，1)，对2017年第一季度客流量进行状态预测，由一步状态转移得到

P(1)=V0P=(0，0，1)，

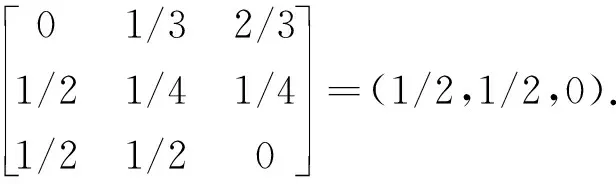
则得到2017年第一季度处于第一状态的概率为1/2，处于第二状态的概率为1/2。通过加权平均得出2017年第一季度客流量预测值为6 550万人。同理，用V0×P2对2017年第二季度客流量进行预测，为7 016万人，用V0×P3对2017年第三季度客流量进行预测，为7 215万人。根据地铁客流量原始值和灰色马尔科夫模型预测值建立对比图，如图1所示。

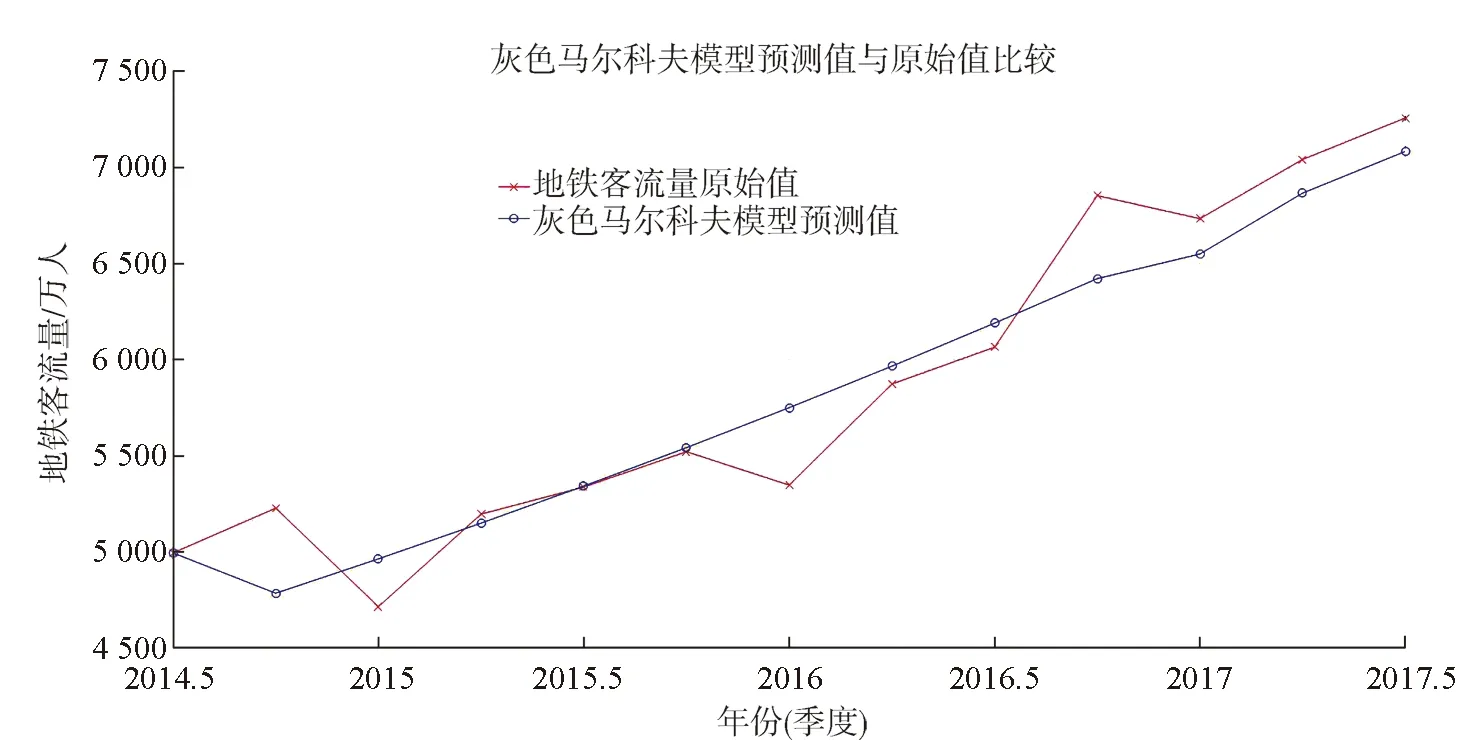
图1 灰色马尔科夫模型对客流量的预测

图1给出了灰色模型对2号线客流量的预测，地铁客流量实际值围绕灰色模型预测值上下波动，整体上看用灰色模型均能够相对准确预测各个季度的客流量，验证了灰色模型的可行性。将2014年第3季度到2016年第4季度的数据当作己知的数据，用马尔科夫预测模型分别对2017年前3个季度的客流量进行预测，从图1中得出灰色马尔科夫模型修正后的灰色GM(1，1)模型，精度进一步提高，能够准确地预测，但模型具有可用性之外也存在一定的误差，需要对灰色马尔科夫预测模型结合实际情况加以改进。

2.2 基于滑动优化的灰色马尔科夫模型

对原始数据序列经一次加权滑动平均处理后建立无偏GM (1,1)模型，称为滑动无偏GM (1,1)模型[15]。滑动无偏GM (1,1)模型对原始数据进行处理，得出滑动无偏GM(1，1)模型的预测值(见表4)。

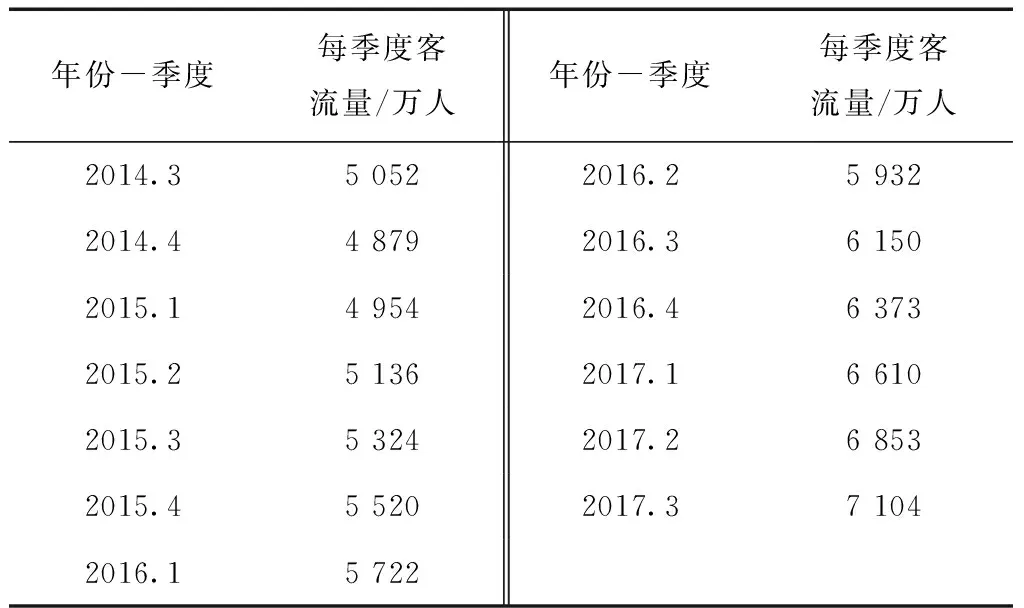
表4 2014.3—2017.3西安地铁客流量滑动 无偏GM(1，1)模型的预测值

由残差的相对值Δ(K)将它们划分为3种状态，分别记为⊕1=(-8%，-2%]，⊕2=(-2%，0]，⊕3=(0，8]， 2014.3—2016.4的GM(1，1)模型的预测值、每年的残差ε(1)(K)、残差的相对值Δ(K)、以及各自所处的状态(见表5)。

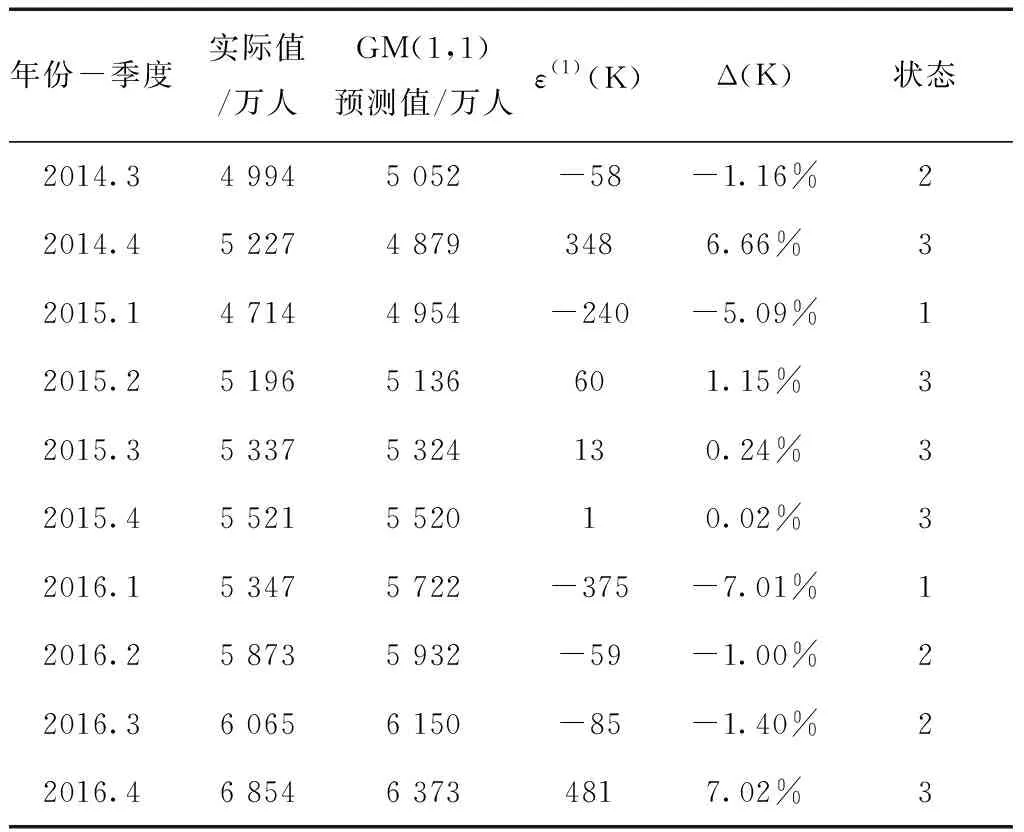
表5 状态分布表

通过GM(1，1)模型与滑动无偏GM(1，1)模型预测结果的对比分析，发现滑动无偏GM(1，1)与传统的GM(1, 1)相比，最大绝对百分误差从8.48%下降到了7%，平均绝对百分误差从3.6%下降到了2.99%。故无偏GM(1,1)模型与传统的GM(1,1)模型相比在精度方面有所提高。

运用马尔科夫模型对滑动无偏GM(1，1)预测值进行修正，通过加权平均得出2017年第1季度客流量最终的预测值为6 687万人。同理，用V0×P2对2017年第2季度客流量进行预测，为6 974万人，用V0×P3对2017年第3季度客流量进行预测，为7 191万人。由此绘制滑动无偏灰色模型预测值和客流量原始值对比图(见图2)。

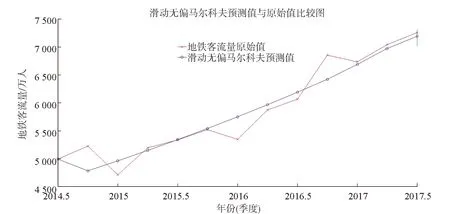
图2 滑动无偏灰色马尔科夫模型对客流量的预测

图2给出了滑动无偏灰色模型对2号线客流量的预测，从图2可知，地铁客流量实际值围绕灰色模型预测值上下波动，且波动幅度进一步缩小。整体上看用滑动无偏灰色模型比传统灰色预测模型更为贴近现实值，验证了滑动无偏灰色模型的优越性；将2014年第三季度到2016年第四季度的数据当作己知数据，用滑动无偏灰色马尔科夫预测模型分别对2017年前3个季度的客流量进行预测，从图中得出马尔科夫模型修正后的滑动无偏灰色GM(1，1)模型，精度进一步提高，能够准确预测，与实际值的误差降到最低。

2.3 马尔科夫模型与滑动无偏马尔科夫模型比较

将地铁客流量原始值、马尔科夫模型预测值和滑动无偏马尔科夫模型预测值建立比较图(见图3)。

图3 两种预测值与实际值的比较

从图3可以看出，利用滑动无偏灰色马尔科夫模型得到的拟合曲线更接近于原始曲线，比灰色马尔科夫模型拟合的曲线效果要好，更倾向于实际数据。

对比2017年3个季度的灰色马尔科夫模型、滑动无偏灰色马尔科夫模型两个模型的评定标准:最大绝对百分误差(MaxAPE),平均绝对误差(MAE)，平均绝对百分误差(MAEP)(见表6)。

表6 预测方法的误差对比

从图3和表6可知，经过滑动无偏灰色马尔科夫模型优化后的3种误差均有所下降，预测精度提高，验证了滑动无偏灰色马尔科夫预测模型在地铁客流量预测中的适用性。

3 结 语

本文将滑动平滑法和无偏GM(1，1)方法结合，对原始的灰色GM(1，1)进行改进，应用于地铁客流量的预测，构建了滑动无偏灰色马尔科夫预测模型对地铁客流量预测模型，并与原始的灰色马尔科夫预测模型进行预测效果比较。利用模型对西安地铁二号线客流量进行预测，并与原始的灰色马尔科夫预测模型进行预测效果比较。实验结果表明，滑动无偏灰色马尔科夫预测模型的预测精度均较高，最大绝对百分误差(MaxAPE)、平均绝对误差(MAE)、平均绝对百分误差(MAEP)均比原始的灰色马尔科夫模型预测结果有了一定的提升，验证了滑动无偏灰色马尔科夫预测模型在地铁客流量预测上的适用性。