薄柔H形截面钢构件在横向冲击下的局部屈曲破坏
2018-11-15陈鹏程路国运杨会伟
陈鹏程,路国运,杨会伟,张 恩
(太原理工大学 建筑与土木工程学院,太原 030024)
薄柔构件的截面拥有较大的宽厚比,单位长度的质量一定时,薄柔截面构件相对厚实截面构件具有更大的回转半径、惯性矩、抗弯刚度及弹性整体稳定性,材料利用率高,经济性能指标较好。因此,薄柔构件通常作为建筑结构的主要承重构件,如低层住宅结构体系的屋架、厂房和体育场馆的钢框架,石油化工设备的构件等[1-3];也可作为安全防护的吸能构件,如汽车保险杠、高速公路的防护栏[4-6]。这些结构在服役过程中可能会受到意外荷载的撞击,所以评估其耐撞性及损伤就显得尤为重要。通过对碰撞事故的调研发现[7],有90%的受损构件发生弯曲变形破坏。因此,对于薄壁结构在横向冲击作用下的弯曲行为研究具有非常重要的意义。
薄壁构件在横向冲击荷载作用下,易产生局部屈曲变形,即撞击处横截面壁会产生塑性弯折。关于薄壁构件的弯曲破损,KECMAN[8]最早提出了方钢管弯曲破坏的塑性铰线理论模型,模型假设撞击能量被塑性铰线吸收,并将铰线分为固定塑性铰线和移动塑性铰线,分别计算两类铰线吸收的能量,并与不同截面尺寸的方钢管弯曲破坏试验进行了对比,验证了理论模型的有效性。随后,KIM et al[9]对该模型进行了改进,为了使机构达到运动许可,他们在侧壁突出处采用了环状曲面,通过总能量极小化处理,得出了滚动半径等未知参数。TANG et al[10]对不同截面类型的薄壁构件进行了理论及数值模拟分析,重点研究了截面几何尺寸、截面类型(箱形、帽形、圆形、椭圆形)对构件耐撞性等参数的影响,如能量吸收、撞击平均力、峰值力。此外,还有学者将泡沫铝[11-13]、蜂窝铝[14]、聚氨酯[15]等轻质材料填入薄壁构件中用做防护结构;试验结果表明,冲击荷载作用下该复合结构易发生局部屈曲且局部变形可以吸收大部分的冲击能量。在此基础上,通过理论、试验及数值模拟的方法进一步研究该复合结构的抗冲击性能。针对H形截面钢构件受横向冲击的研究,霍静思等[16]设计了热轧H形钢梁落锤冲击试验,分析了落锤冲击速度和冲击能量对钢梁动态抗冲击力学性能的影响规律。崔娟玲等[17]完成了两种不同边界约束条件下的热轧H形钢柱横向冲击试验,研究了钢柱在不同冲击能量作用下的抗冲击性能。
由上可知,关于薄柔构件的弯曲破坏研究,其截面构型主要集中在方管、圆管及填充相关轻质材料的复合结构,H形截面研究较少且所选构件截面较为厚实。而薄柔H形钢由于截面分配合理,在工程领域已得到广泛应用。为评估其在冲击作用下的损伤,本文建立了薄柔H形钢构件在横向冲击作用下的局部屈曲破坏理论模型,利用有限元模拟对理论模型进行了验证,在此基础上,进一步分析了截面几何参数对构件抗冲击性能的影响。
1 理论模型建立
薄壁构件的弯曲变形理论以塑性铰线理论较为常用。本文主要建立了H形截面构件的塑性铰线理论模型,由于构件塑性变形较大,冲击载荷所做的功大部分以塑性变形能的形式耗散掉。为了兼顾计算精度和数学解法,本文将材料模型简化为理想刚塑性,同时假定弯曲引起的构件的局部变形只沿直的铰线发生,变形部分不可伸长。
构件的能量吸收可通过弯曲受损截面中每条塑性铰线吸收的能量来确定,即
(1)
式中:θ为塑形铰所在截面转过的角度。
图1为构件弯曲变形截面的塑性铰线分布,共10根,其中包括位于翼缘的铰线:GH,EF,BC,IM,JK,DM;腹板的铰线:IA,JA,AK,AN.图2为构件变形腹板的正视图和侧视图,由几何关系可得N点坐标为:

(2)
式中:ρ为构件转过的角度,l为塑性铰区的长度。

图1 塑形铰线模型Fig.1 Yield line model for H sections

图2 腹板塑形铰线图Fig.2 Yield line model for web of H sections
因为变形截面长度保持不变,由yN=yA得:
(3)
利用原平行于构件轴线并通过A的纤维的纵向连续性,并注意到l对于任意的ρ都成立,由此得到塑性铰区的长度l.
双师协同教学模式一方面体现了开放的思想,不管是“学科双师”协同模式,还是“虚实双师”协同模式,都充分利用网络资源,使我们的课堂内容不再仅仅局限于教材;另一方面也体现了整合的思想,既是学科间的整合,又是人文、艺术、科学等跨领域的整合,不仅贯彻在课程上,更是贯彻在课堂上,做到了课程与课堂同步。
下面来确定每条塑性铰线吸收的能量,受压翼缘塑性铰线GH和EF处的转角为α.
因此,GH和EF吸收的总能量为:
W1=WEF+GH=2M0fbα.
(4)

(5)
对于翼缘铰线BC,转角为π-2β,因此BC吸收的总能量为:
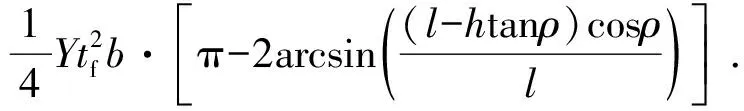
(6)
对于腹板铰线AN,其长度为zA,转角为π-2β,因此吸收的总能量为:

(7)
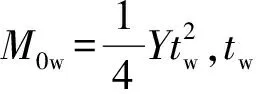
对于腹板铰线IK,JK,其转过的角度为η.利用三角形全等定理,将空间二面角η转化为平面角,如图3所示。具体做法如下:过N作垂直于JK的平面ω,N1为N在JK上的投影。将ω逆时针旋转一定角度ψ,对于该平面内的一点N2,N为N2的投影,当N2N=zA时,ψ=η.

图3 铰线GK转过的角度ηFig.3 Angle η of rotation along the line GK
W4=WIK+JK=2M0w·IK·arctanη.
(8)
式中,η可由下式计算:
(9)
腹板顶部两根铰线IA,JA所吸收的能量等于铰线所扫过的面积乘以平均曲率和M0w,即:
(10)
式中:r为腹板突出处的曲率半径。根据文献[8]并结合大量数值模拟结果得其表达式为:
(11)
对于腹板铰线AK,其转角为ξ,因此吸收的总能量为:
W6=WAK=M0w·AK·arctanξ.
(12)

(13)
最后,底部翼缘塑性铰线KM,KD吸收的能量为:
W7=WDM=M0f·b·ρ.
(14)
故所有铰线塑性弯曲吸收的能量由全部7个能量分量求和可得:
(15)
而该塑性铰转角θ=2ρ,利用上式将ρ进行替换,便可得到构件能量吸收与塑性铰转角的关系。
2 模型校验
2.1 模型建立
采用ABAQUS/explicit对冲击过程进行模拟,图4为H形钢构件受横向撞击的有限元模型。
钢材的力学性能由双线性强化模型来描述,屈服强度取fy=345 MPa,极限强度取fu=495 MPa,弹性模量E=2.06×105MPa,强化段切线模量取Eh=E/100=2.06×103MPa,泊松比为0.3.由于应变率对钢材的屈服强度有显著影响[18],因此需要考虑应变率效应。选用Cowper-Symonds模型[18],模型如式(16)所示:
(16)
式中:σd为材料在塑性应变率εp下的动态应力值;σ0为相应的静态应力值;D和q是与材料类型有关的常数,对于低碳钢一般取D=40.4 s-1,q=5[18]。

图4 有限元模型及截面几何参数Fig.4 Finite element model and the geometry of H beam
采用动态耦合(kinematic coupling)将左右两端截面的所有节点耦合在参考点上,约束参考点的线位移Ux,Uy及绕y轴和z轴的转动位移Ry,Rz四个自由度,允许其沿轴向运动及绕x轴的转动。在锤头上定义初始速度实现冲击载荷的加载。冲击物与构件之间的接触定义为无摩擦的面-面接触,使用动力学接触方法。在相同的网格密度下,壳单元比实体单元更节省计算时间和内存,因此,构件采用四节点减缩积分格式的三维壳单元(S4R)进行网格划分。为了保证计算精度,对着重分析的关键部位(构件全长的1/5)做网格加密处理,网格大小为10 mm.冲击物采用实体单元(C3D8R)进行网格划分,由于模拟撞击过程中冲击物变形很小,且其变形对计算结果影响很小,因此利用Rigid Body将冲击物刚性化。
2.2 结果对比
以截面尺寸300 mm×200 mm×6 mm×8 mm为例,冲击能量为50 kJ,模型共计13 231个单元。将数值仿真结果与理论分析结果进行对比,结果如图5和表1所示。由图5可以看出,随着截面塑性铰转角的增加,构件吸收的能量逐渐增大,但吸收的速率逐渐减缓。开始阶段,理论所得构件吸收的能量比模拟稍大,这可能是因为构件在变形初始时,移动塑形铰线还未产生。
通过有限元模拟与理论模型的对比分析结果可知,二者误差小于10%,说明理论模型较为合理,可以很好地描述薄柔H形构件在横向冲击作用下的局部屈曲破坏。

图5 理论与模拟对比Fig.5 Comparison between therotical model and FEM

对比项理论值模拟值理论值/模拟值位移/mm387.46387.650.999 5能量/kJ25.7925.850.997 7平均力/kN66.5666.680.998 2
3 讨论
为了更深入地探究薄柔H形构件在冲击作用下的弯曲性能及能量吸收特性,本文通过改变截面几何尺寸来对其进行参数分析。固定板件中心线的尺寸,即固定截面高(h=300+tf(mm)),宽(b=200 mm),以及构件长度(L=3 000 mm).设计不同翼缘、腹板厚度的H形钢,分析翼缘、腹板宽厚比对H形钢构件抗冲击性能的影响,冲击能量为50 kJ.所选构件符合实际工程应用。H形构件在冲击作用下的弯曲性能及吸能特性,可通过平均力、比吸能两个指标进行评价。
平均力,是指外载荷作用下截面的塑性弯曲变形δ内单位位移所吸收的能量:
(17)
比吸能为构件在塑性弯曲变形δ内单位质量所吸收的能量:
(18)
不同翼缘厚度H形截面构件的能量吸收如图6所示。随着变形位移的增加,构件吸收的能量逐渐增大,但能量吸收的速率逐渐减缓。翼缘厚度的增加使得构件吸收的能量逐渐增大,且构件能量吸收的速率逐渐加快。这是由于翼缘厚度的增加使得截面的抗弯强度增大,对于弯曲耗能为主的构件,相同弯曲位移下翼缘越厚,吸收的能量越多,因此吸收速率越快,构件抗冲击能力越强。
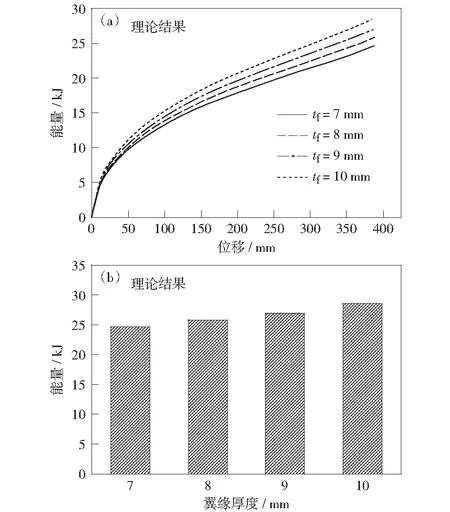
图6 翼缘厚度对构件能量吸收的影响Fig.6 Effect of flange thickness on energy dissipation
腹板厚度对构件能量吸收的影响如图7所示。随着腹部厚度的增加,构件吸收的能量逐渐增大,且构件能量吸收的速率逐渐加快。这是由于腹板厚度的增加使得截面的抗弯强度增大,对于弯曲耗能为主的构件,相同弯曲位移下腹部越厚,吸收的能量越多,因此吸收速率越快,构件抗冲击能力越强。翼缘厚度从7 mm增加到10 mm,增加42.9%,能量吸收增长15.9%;而腹板厚度从4 mm增加到5 mm,增加25%,能量吸收增长37.6%。说明在冲击能量一定的情况下,如果腹板、翼缘增加相同的幅度,腹板厚度对构件能量吸收的影响要大于翼缘厚度的影响,进一步说明了薄柔H形截面钢构件受沿弱轴方向冲击产生局部屈曲变形时,腹板为主要的耗能部位。
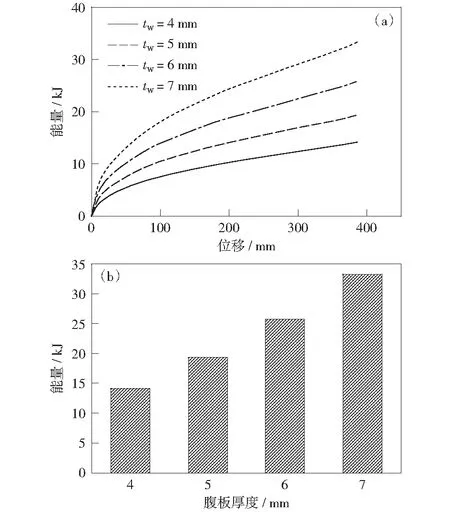
图7 腹板厚度对构件吸量能收的影响Fig.7 Effect of web thickness on energy dissipation
不同翼缘、腹板厚度的比吸能如图8所示。随翼缘厚度的增大,构件的比吸能逐渐降低,但幅度并不明显。这是由于截面翼缘厚度增大时,构件在静力下的截面抗弯强度增大,构件吸收能量增多,但构件质量增涨幅度更为明显,因此构件的比吸能呈降低趋势。随腹板厚度的增大,构件的比吸能呈明显的上升趋势,这是由于构件截面腹板厚度增加所引起的构件质量增涨速率低于构件能量吸收速率,因此构件的比吸能逐渐增大。
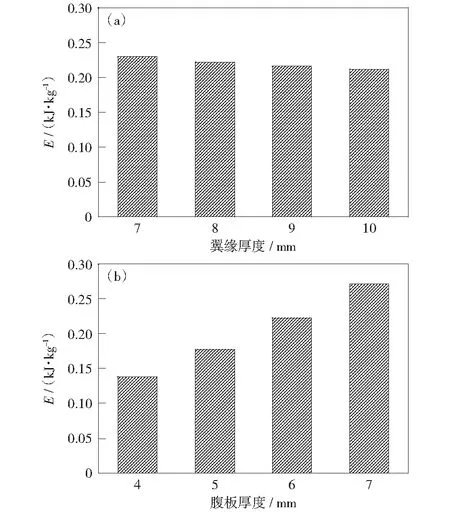
图8 截面几何参数对构件比吸能的影响Fig.8 Effect of geometry on SEA
4 结论
本文主要对薄柔H形截面钢构件在横向冲击荷载作用下的局部屈曲进行了理论研究,得到了构件的能量吸收与塑性铰转角的关系。同时建立了精确的有限元模型,并对理论所得构件的能量吸收、平均力、位移做了对比。在此基础上,利用理论模型研究了截面几何参数对构件弯曲性能及吸能特性的影响。结果表明:
1) 当塑性铰转角增加时,构件吸收的能量逐渐增大,但能量吸收的速率逐渐减缓。
2) 随着腹板和翼缘厚度的增大,构件吸收的能量逐渐增大,且构件能量吸收的速率逐渐加快;这是由于腹板、翼缘厚度的增加使得截面的抗弯强度增大,耗能增加。进一步分析可知薄柔H形截面钢构件受沿弱轴方向冲击时产生局部屈曲变形,腹板为主要耗能部位。
3) 由于翼缘厚度的增大使得构件质量增长的速率高于构件能量吸收的速率,因此,构件的比吸能逐渐降低,但幅度并不明显。而随着腹板厚度的增大,由于构件截面腹板厚度增大所引起的构件质量增长速率低于构件能量吸收速率,因此腹板厚度的增加使得构件的比吸能逐渐增大。
