一种改进的ELM-LRF图像分类方法
2018-11-15赵志宏续欣莹
赵志宏,续欣莹,陈 琪,谢 珺
(太原理工大学 a.电气与动力工程学院;b.信息与计算机学院,山西 晋中 030600)
图像分类作为图像检索和机器人视觉的基本任务[1],在计算机视觉和机器学习中受到广泛的关注。图像分类的研究主要有预处理、特征提取和分类器训练三个方向[2]。在特征提取方面,国内外学者提出了LBP、HOG、稀疏编码等[3]方法;在分类器训练方面提出了神经网络、决策树、极限学习机以及支持向量机(SVM)等[4]多种分类方法。传统图像分类方法通过特征提取采得图像的各种特征,之后将提取到的特征利用分类器进行分类,从而达到图像分类的目的。对于不同的数据集,传统方法的特征提取与分类器均是通过实验人工选取的,算法的普适性较差[5]。
近年来提出的深度神经网络[6]由于其优异的性能在计算机视觉的各个领域得到广泛的研究。其中卷积神经网络(CNN)[7]由于其考虑了图像的二维结构信息以及强局部关系,在图像分类领域性能较为突出。CNN摒弃了传统分类方法先特征提取后分类的思维定势,将两者合并。利用设定好的网络结构,完全从训练数据中学习图像的层级结构性特征,能更加接近图像的高级语义特征。因此也得到了广泛的研究。2012年的AlexNet,2014年的GooleNet、VGG,2015年的Deep Residual Learning,这些根据CNN提出的改进版本从模型深度、组织结构等方面对CNN进行了改进,使得分类精度有所上升[8]。但与此同时,复杂的深层网络结构也使得模型的参数成倍增加,大大降低了使用的便捷性。2015年黄广斌等在极限学习机[9](ELM)基础上受CNN的思想的启发,构建了基于局部感受野的极限学习机(ELM-LRF)[10]。ELM-LRF仅有一个隐含层(包含一个卷积层和一个池化层),模型参数和训练时间均较CNN大大减小,分类精度也很高;但由于网络的特征图输入权重是随机产生的,稳定性有待增强[11]。
本文提出了一种改进的ELM-LRF算法。利用粒子群算法优化选择ELM-LRF算法卷积过程中各个特征图的输入权重,将逐次迭代后得到的最优特征图权重作为最终分类网络的参数,避免了复杂的人为选取参数过程,使用更加便捷。在数据库Caltech 101 dataset[DB/OL][12]和CIFAR-10上将本文算法与其他算法进行比较,实验结果表明改进的ELM-LRF算法不仅提高了算法的稳定性,还充分发挥了粒子群的全局优化能力,大大提高了分类精度。
1 传统ELM-LRF算法
1.1 极限学习机(ELM)
极限学习机(ELM)是2004年新加坡南洋理工大学黄广斌等人提出的一种新型单隐层前馈神经网络(SLFNs)[13]。该算法无需复杂的迭代计算,只需要设置隐含层节点个数,网络便能通过随机输入权重和隐含层偏置产生唯一的最优解,参数选择容易、学习速度快而且泛化性能好[9]。
ELM求解过程如下:对于n个任意的样本(xi,ti),其中xi=[x1,x2,…,xn]代表第i个输入向量,ti=[t1,t2,…,tn]表示第i个训练样本的目标标签,则一个具有L个隐含层节点,激励函数为G(x)的前馈神经网络的输出可以表示为:
(1)
式中:wi=(wi1,wi2,…,win)T是第i个隐含层节点与训练样本之间的权重;bi是第i个隐含层节点的偏置;βi=(βi1,βi2,…,βim)T是第i个隐含层节点和输出节点之间的权重;Yi=(y1,y2,…,yn)T是输出期望向量。
ELM的目标是最小化输出与期望的误差。上述等式可以表示为:
Hβ=L.
(2)
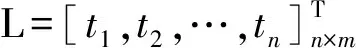
最后使用最小二乘法来计算输出权重,如下式:
(3)
式中,H+是H的广义逆矩阵。
1.2 基于局部感受野的极限学习机(ELM-LRF)
基于局部感受野的极限学习机(ELM-LRF)是一种特殊的ELM。其架构中输入层和隐含层节点之间的连接是根据连续概率分布随机生成的,这种随机的连接构成了局部感受野[10]。ELM-LRF通过类似卷积神经网络(CNN)的单层卷积、池化网络来自行提取输入中的特征,并且通过ELM的输出权重公式进行分类,具体结构如图1所示。

图1 ELM-LRF精简架构Fig.1 Simple architecture of ELM-LRF
为了更充分地表示输入,采用K个不同的输入权重,从而得到K个不同的特征图[14],如图2所示。其具体实现分为以下3个步骤:
1) 随机生成初始权重Ainit.设输入图像大小为d×d,局部感受野大小为r×r,那么特征图的大小为(d-r+1)×(d-r+1).
(4)
之后采用奇异值分解(SVD)将初始权重Ainit正交化,记正交化的结果为A,A中每一列αK都是Ainit的一组正交基。第k个特征图的输入权重是αk∈Rr×r,由αk逐列排成。第k个特征图的卷积节点(i,j)的值ci,j,k由下式计算:

(5)
2) 平方根池化。池化大小e表示池化中心到边的距离[15],在ELM-LRF中池化图与特征图大小相同,都为(d-r+1)×(d-r+1).ci,j,k和hp,q,k分别表示第k个特征图中的节点(i,j)和第k个池化图中的组合节点(p,q).
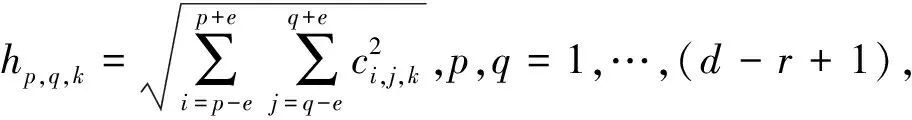
(6)
3) 计算输出权重矩阵。对于每一个输入样本x计算其对应的特征图和池化图,并把池化图中的各个组合节点合成一个行向量;之后将N个输入样本的行向量连接起来,得到组合层矩阵H∈RN×Kg(d-r+1)2,最后组合层与输出层采用全连接。输出权重为β,采用正则化最小二乘解析计算。具体公式如下[10]:
如果N≤Kg(d-r+1)2
(7)
如果N>Kg(d-r+1)2
(8)
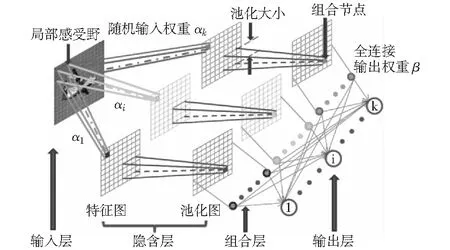
图2 含K个特征图的ELM-LRF网络架构Fig.2 Architecture of ELM-LRF with K maps
2 粒子群(PSO)算法
粒子群算法又叫鸟群算法,其思想源于鸟群觅食行为,每个粒子代表一组可能的解,所有的粒子组成一个群体,粒子在空间中根据自身的历史信息和群体的历史信息决定自己的速度和位置,直到找到问题的最优解,其迭代更新公式[16]如下:
(9)

为使算法前期拥有较好的全局搜索能力,在较大区域内寻找最优解,后期拥有较好的局部搜索能力,在局部精细搜索,采用惯性权重线性下降处理,如式(10)所示[17]:
(10)
式中:wmax,wmin分别为权重最大值和最小值;kn和kmax分别为当前和最大迭代次数。
3 改进的ELM-LRF算法
本文提出的改进ELM-LRF图像分类算法是运用PSO算法对传统ELM-LRF算法中随机生成的K个特征图的初始权重Ainit进行优化选择,最终选取最优值作为模型的参数。与常规PSO优化ELM网络不同的是,本文通过PSO改进的ELM-LRF算法(命名为IPSO-ELM-LRF)针对图像强的局部关系以及二维结构信息,优化的参数为ELM-LRF算法中各个卷积核的初始权重,由于卷积核的加入,使得优化后的算法比传统经PSO优化的ELM对图像有更强的针对性。IPSO-ELM-LRF的算法流程如图3所示。
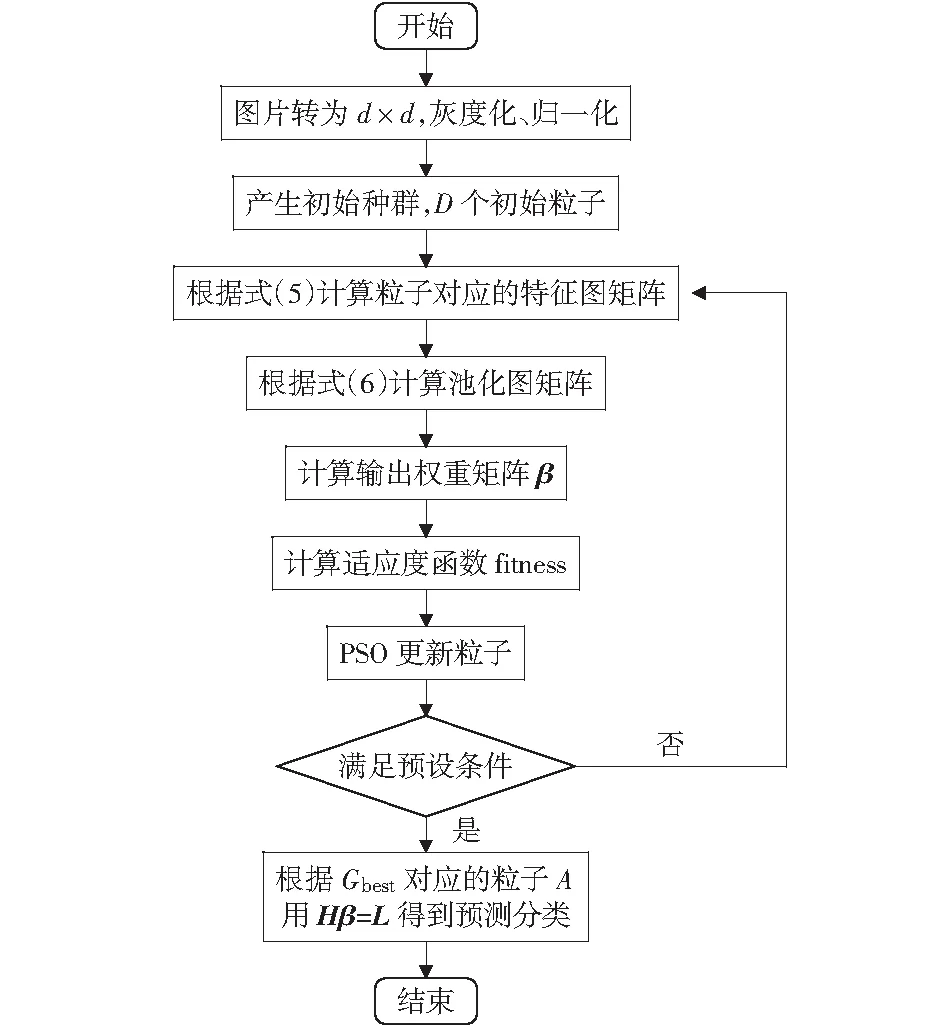
图3 IPSO-ELM-LRF算法流程图Fig.3 Arithmetic flow chart for IPSO-ELM-LRF
具体步骤为:
1) 将图像转化为d×d大小,之后将图像灰度化、归一化作为算法的输入样本。
2) 产生初始种群:根据感受野大小(r×r)和特征图数量K产生D=(r×r)gK个初始粒子。
3) 根据式(5)计算粒子对应的特征图矩阵。
4) 根据式(6)计算池化图矩阵。
5) 计算粒子对应的输出权重矩阵β(式7)。
6) 计算适应度函数:首先根据Hβ=L计算出预测标签L,适应度即为图像的分类准确率。第i个粒子的适应度记为fitness_i(注:对于第一个粒子A1,令最优适应度值fitness_best=fitness_1,并将A1作为个体最优值PBest)。
7) PSO更新粒子:
由式(9)—(10)更新种群中各粒子的速度和位置。然后执行下列伪代码:
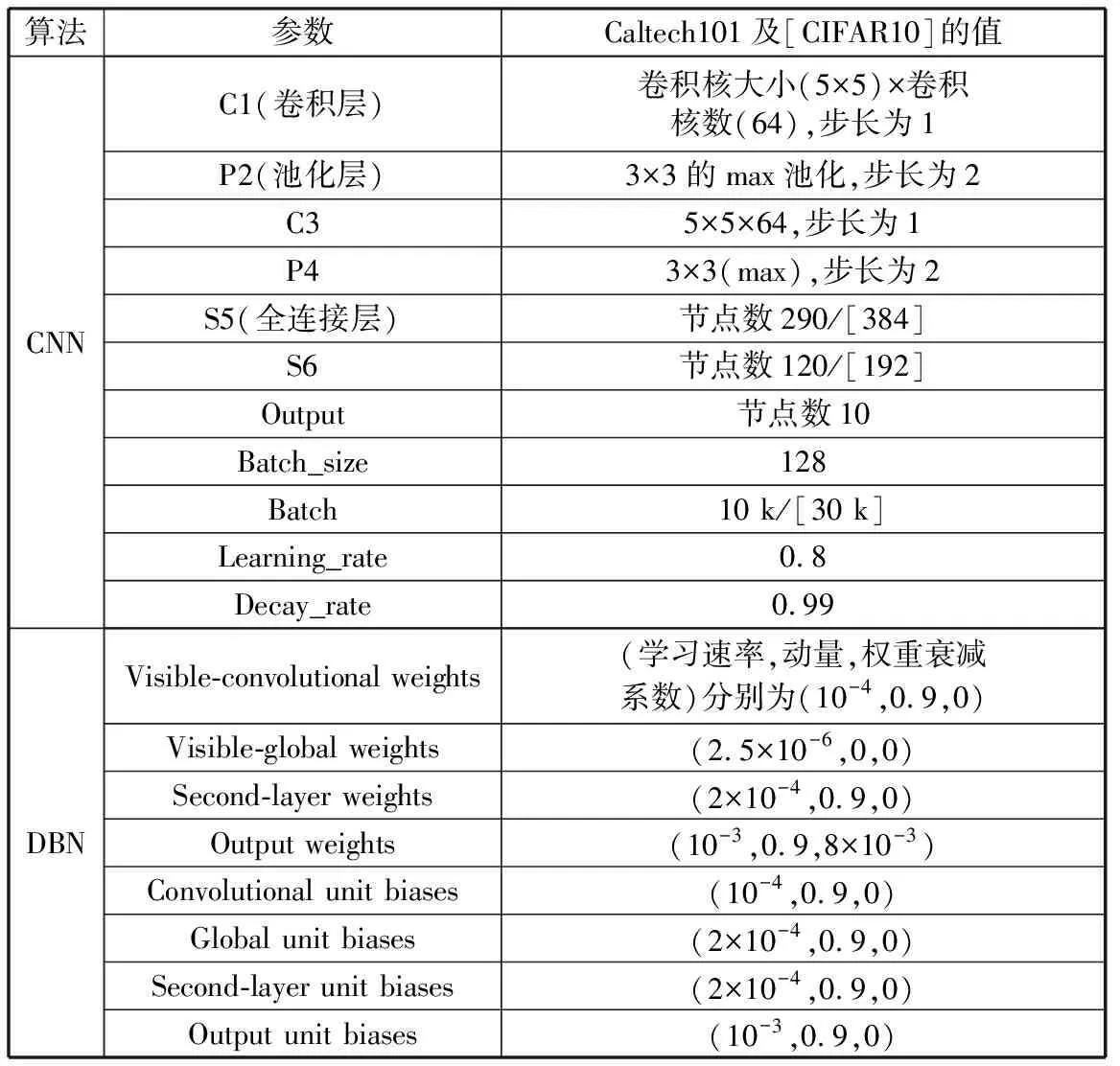
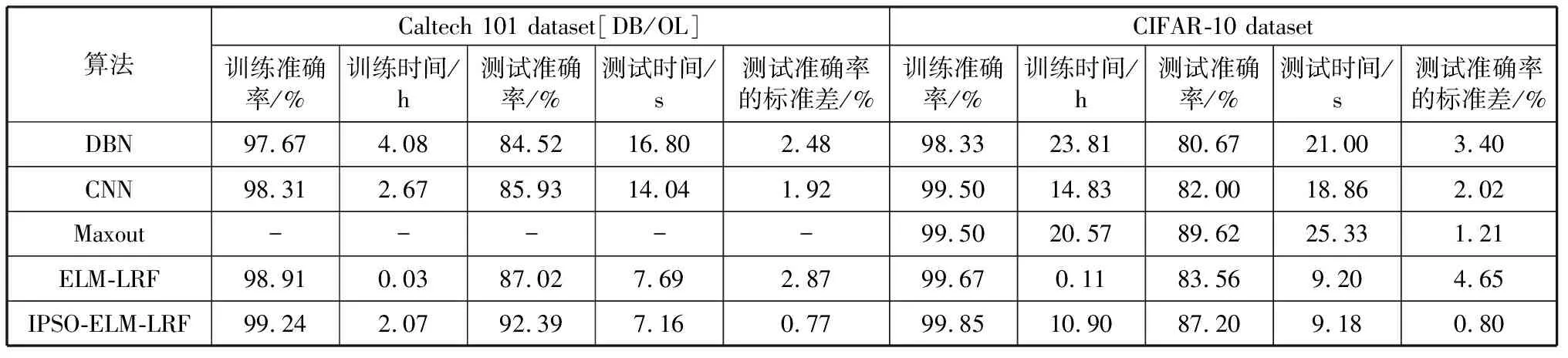
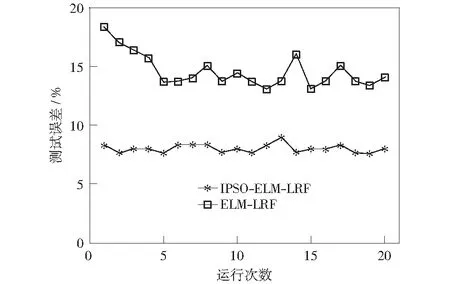
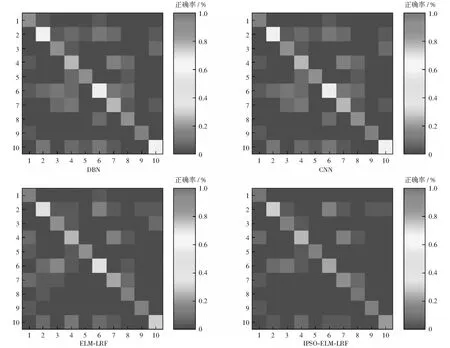
For (1 // popsize为种群中的粒子个数 { 计算Ai的适应度值fitness_i; If fitness_i>fitness_best PBest(i)=Ai fitness_best=fitness_i Else } 令fitness_best对应的粒子A为全局最优值GBest; 8) 满足预设的迭代次数或者GBest达到预设值,进入下一步,否则转到3)。 9) 得到GBest对应的粒子(输入权值),利用ELM-LRF求得输出权值矩阵。由Hβ=L计算出预测类别。 需要注意的是,第7)步中,随着粒子的更新,其粒子位置可能超出预先规定的位置上下限Xmax,Xmin.本文采用如下方式进行约束:若粒子位置大于上限Xmax,则让其等于上限;若粒子位置小于下限Xmin,则让其等于下限。由于粒子是由高斯分布随机数产生,故这里规定其位置上下限为±3. 为了验证IPSO-ELM-LRF算法的有效性,我们在以下两个数据集上进行图像分类实验。数据集一为Caltech 101 dataset[DB/OL][12],该数据包含101类物体图像。为了方便与其他算法作对比,本文选取了该数据库官方给出的常用10个类,分别为Airplane, Bonsai, Car_side, Chandelier, Face,Hawksbill,Ketch,Leopards,Motorbikes,Watch.每类包含123~800幅图像,每类图像具有复杂的背景且大小不一,其中还夹杂大量灰度图像,这给常规分类算法带来了一定的挑战。为保证公平的测试条件,根据常规的实验设定,本文从每类中随机抽取100个样本,并通过下述方法进行数据增强:1) 水平和垂直方向作镜像处理;2) 将图像分别沿上、下、左、右、左上、左下、右上、右下八个方向进行5个像素点的平移,平移之后的空白用0补全。通过上述两种方法将数据集扩充为原来的10倍,共10 000张图像,选择其中7 000幅用做训练图像,1 500幅用做优化算法的验证图像,剩余的1 500幅作为实验最终的测试图像。 数据集二为CIFAR-10 dataset,该数据集包含Bird,Cat,Frog等10类图像,每类图像6 000幅。本文随机选择每类的5 000幅图像为训练集,500幅为验证集,剩余500幅为测试集。将两个数据集图像均转化为32dip×32dip, 之后将图像灰度化、归一化作为输入样本。 本文提出的IPSO-ELM-LRF算法中,最重要的有两类参数,一类是ELM-LRF中的平衡参数C和特征图个数K,另一类是优化算法中的种群大小P和迭代次数N.对于惯性权重w、学习因子c1和c2等相关参数的选取,已较为成熟稳定,本文参照文献[18]中的相关参数设置。具体数值如表1所示。 表1 IPSO-ELM-LRF算法的相关参数Table 1 Related parameters of IPSO-ELM-LRF 为了分析平衡参数C和特征图个数K对算法的影响,本文首先做了参数敏感性实验。将变量C的范围设定在{10-4,10-3,10-2,…,102,103},K的范围设定在{12,24,36,48,60},在此基础上分析参数对算法的影响。结果如图4所示。图中可以看出:对于Caltech 101 dataset,当C=0.01,K=48时,测试准确率最高;对于CIFAR-10 dataset,当C=0.1,K=48时,准确率最高。 图4 IPSO-ELM-LRF算法中C,K参数敏感性测试Fig.4 Sensitivity test of C and K parameters in IPSO-ELM-LRF algorithm 针对种群大小P和迭代次数N对算法的影响,本文首先设置IPSO-ELM-LRF的迭代次数为10,种群大小分别选择P=5,10,15,…,40,每次实验做20组取平均值(下同),测试IPSO-ELM-LRF的测试误差,测试结果如图5所示。可见对于2个数据集,当种群大小分别为20和30时,生成最优解。 图5 种群大小对测试误差的影响曲线Fig.5 Influence curve of population size on test error 设置Caltech 101 dataset种群大小为20,CIFAR-10 dataset种群大小为30,将迭代次数逐渐增大。由图6可见,随着迭代次数的增加,测试误差逐渐减小。Caltech 101迭代次数为90时,趋于平稳;CIFAR-10迭代次数为105时,趋于平稳。 图6 迭代次数对测试误差的影响曲线Fig.6 Influence curve of iteration times on test error 为验证IPSO-ELM-LRF算法在图像分类上的性能,在上述两个数据集上,本文将该算法与传统ELM-LRF以及其他深度学习算法进行了比较。其中IPSO-ELM-LRF采用表1的参数,相应的传统ELM-LRF算法中的平衡参数C、特征图个数K、核大小Ke和池化大小e也与表中参数相同。CNN和DBN的模型参数参照文献[19-20]设定,具体参见表2。实验在Intel 2.5 GHz CPU,64G RAM和Matlab R2015a环境下进行。实验运行20次后取平均值进行对比,实验结果如表3所示。 表2 CNN与DBN分类时的相关参数Table 2 Related parameters in the classification of CNN and DBN 对于Caltech 101数据集,在测试准确率方面本文提出的IPSO-ELM-LRF算法达到了92.39%,比传统ELM-LRF算法高5.37%,且均高于经典的深度学习算法CNN和DBN;在训练时间方面,传统ELM-LRF算法的训练时间远远小于其它3种算法,比用时最长的DBN缩短近百倍,这也对其进行优化提供了条件;测试时间方面,IPSO-ELM-LRF算法优于其它3种算法,说明其在实际预测过程中有较为优秀的性能;在测试准确率标准差方面,传统ELM-LRF算法最高,达到了2.87%,通过本文改进后降为0.77%。综上,本文提出的IPSO-ELM-LRF算法虽然训练时间比传统ELM-LRF算法上升,但其准确率和稳定性均大大提高,且其训练时间与DBN和CNN相比仍占据优势。 表3 不同算法分类结果对比Table 3 Comparison of classification results of different algorithms 对于CIFAR-10数据集,在训练准确率方面,五种算法几乎都达到了100%;在测试准确率方面ELM-LRF算法的准确率略高于CNN和DBN,而改进之后的IPSO-ELM-LRF算法准确率达到了87.20%,虽然与该数据集官方给出的89.62%(Maxout算法[21])有一定的差距,但也相差甚微;训练时间方面,在相同实验环境下ELM-LRF的训练时间远远小于传统深度学习方法。本文提出的IPSO-ELM-LRF算法通过迭代寻优提高了传统ELM-LRF的准确率,虽然训练时间也相应地增大,但由于ELM-LRF较快的训练速度,使得迭代寻优后的IPSO-ELM-LRF算法在训练时间上仍要优于传统深度学习算法。测试准确率方面表现最优的Maxout算法训练耗时也比本文提出的算法要长。分析Maxout的原理可知,该算法是通过Kn(人工设定)个隐层节点计算激活值,最终选取Kn个值中的最大值作为输出。Kn的设定使得Maxout的层间参数扩大了Kn倍,从而使得训练时间也成倍增加。测试时间方面,IPSO-ELM-LRF与传统ELM-LRF时间近似,均远远小于其它3种深度学习算法;测试准确率标准差方面,IPSO-ELM-LRF算法同样也较ELM-LRF算法大大降低。 因此可以说IPSO-ELM-LRF算法在准确率、稳定性等方面均优于传统ELM-LRF;而且与CNN和DBN相比,本文的IPSO-ELM-LRF算法在分类性能、训练时间和测试时间上也表现得更为优秀。 图7为Caltech 101数据上IPSO-ELM-LRF与传统ELM-LRF之间的稳定性比较。由图可见,IPSO-ELM-LRF的稳定性稳定在1%以内,性能优于传统ELM-LRF. 图7 IPSO-ELM-LRF与ELM-LRF的稳定性对比Fig.7 Stability comparison between IPSO-ELM-LRF and ELM-LRF 为了更清晰地观察分类结果,本文绘制了Caltech 101数据集10个类的混淆矩阵图,如图8所示。纵轴表示实际标签,横轴表示预测标签。图中混淆矩阵对角线上的颜色越红(深),对角线以外的杂点越少,代表该类的分类正确率越高。因此在图中进一步看出IPSO-ELM-LRF比传统ELM-LRF及其他深度学习算法有更为精确的分类结果。 图8 各算法的混淆矩阵图Fig.8 Confusion matrix graph of each algorithm 针对传统ELM-LRF算法稳定性较差的缺陷,提出一种基于粒子群优化的ELM-LRF算法IPSO-ELM-LRF.利用粒子群优化选择ELM-LRF的输入权重,不仅增强了算法的稳定性,还充分发挥了粒子群的优势,大大提高了分类的准确率。此外本文还给出了IPSO-ELM-LRF参数选取的具体步骤,根据该步骤可快速找到IPSO-ELM-LRF算法针对不同数据集的最佳参数。与常规深度学习算法相比,IPSO-ELM-LRF算法的参数较少,无需复杂的人工参数选取,使用非常便捷,准确率也显著升高。4 实验及实验结果
4.1 数据来源
4.2 参数选取

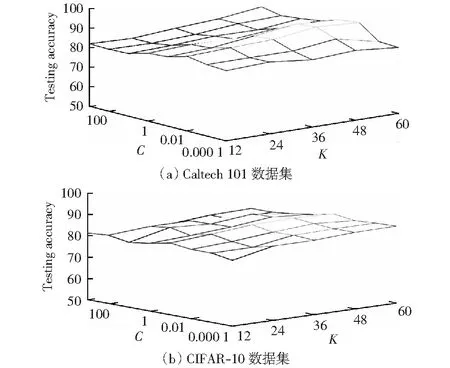
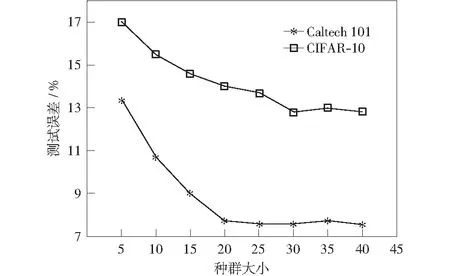
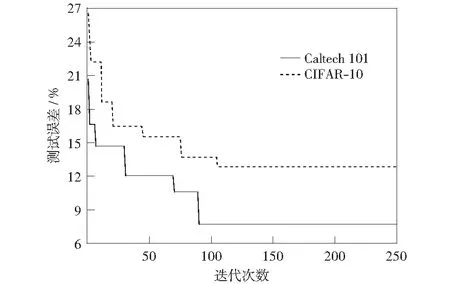
4.3 结果与分析
5 结束语
