高斯混合模型下的相关子空间与离群数据挖掘
2018-11-15樊盼盼张继福
樊盼盼,张继福
(太原科技大学 计算机科学与技术学院,太原 030024)
1 引 言
离群数据是数据集中可能包含一些数据对象,它们与数据的一般行为或模型不一致,蕴含着大量不易被发现却很有价值的数据[1],并已经被广泛运用于电信[2]、灾难气象预报[3,4]、金融[5,6]、网络入侵检测[7]等.随着人们对离群数据挖掘重要性认识的不断加深,以及其离群数据挖掘越来越广泛的应用,日益受到重视,成为数据挖掘领域的研究热点之一.在大多数情况下,离群数据与正常数据在局部数据集中的密度是存在差异的[8],有些属性维上,密度差异较大(稀疏性),另一些属性维上,密度差异比较小(稠密性),密度差异不明显的属性维对度量离群数据几乎是无关的.因此,寻找和删除高维数据集中密度差异较小的稠密子空间,可以有效地降低“维灾”的干扰,并能有效地发现隐藏的离群数据.
相关子空间是一种与离群数据有关的属性集维集合[9],可在相关子空间中有效地度量离群数据,从而可有效地降低“维灾”的影响,但如何选择和度量相关子空间是关键.现有相关子空间的选择和度量都存在着时间复杂度高、依赖于数据分布、参数选择等局限性.高斯混合模型是用高斯概率密度函数精确地量化事物,可以将一个将事物分解为若干的基于高斯概率密度函数的模型[21],可有效地识别高维数据集中密度差异较大(稀疏)的属性集合和密度差异较小(稠密)的属性集合,适用于不同分布的数据.本文针对高维离群数据,给出了一种相关子空间中的离群数据挖掘算法.该算法首先利用稀疏度和高斯混合模型,确定数据对象的相关子空间和不相关子空间,有效地避免稠密数据对挖掘精度和效率的影响;其次,在相关子空间中,利用各个数据的稀疏度和各个属性维的权值来度量数据对象离群值,可以有效的降低“维灾”的干扰;然后,将离群值最大的若干个数据对象视为离群数据;最后,采用人工数据集和UCI数据集实验验证了该算法正确性和有效性.
2 相关工作
传统的离群挖掘方法,例如基于统计[15],基于距离[11,12],基于密度[13,14],基于角度[16]等,都会受到维度的影响,不适用于高维数据,因此将数据投影到相关子空间上再度量离群数据是一种有效的离群挖掘方法.相关子空间法[8,9,17-20],是在数据集中,寻找与离群数据有关的属性集合组成的相关子空间,然后在相关子空间中度量离群数据,包括基于局部参考数据集的线性相关性[17,18],以及基于局部参考数据集的统计模型[8,9,19,20]等.
·线性相关性
Kriegel等人[17]提出了轴平行子空间离群挖(SOD)方法,该方法通过共享最近邻居(SNN)为每一个数据对象寻找一个相似子集,并在相似子集中确定轴平行线性相关子空间,在 SOD 中,仅仅在一个相关子空间中来刻画数据对象的离群程度,当数据对象分布在两个或两上以上的子空间中时,SOD 将不能区分它们的离群程度,显然,在相关子空间中,采用欧式距离的维平均方法度量离群具有明显的不足;Kriegel等人[18]以主成分方法为理论依据,采用马氏距离结合伽玛分布的方法实现了离群数据挖掘,该方法得到的相关子空间是线性相关的任意子空间,相关子空间对线性分布的数据具有很好的适应性,但由于该方法是基于对局部数据分布趋势的偏离,当离群数据所在稀疏区域体现出一种不明显的相关性时,由最大似然估计得到的相关子空间容易出现错误.
·统计模型
Muller等人[8]利用柯尔莫哥洛夫-斯米尔诺夫检验的统计方法,提出了在数据集上选择有意义的子空间方法,从低维到高维采用递归的方式逐步寻找非均匀分布的子空间,并将数据对象在各个相关子空间中的局部离群值累乘,作为该数据对象最终的离群程度,解决了不同子空间中的离群因数可比性问题,但在该算法中,确定所有相关子空间具有维度指数级的时间复杂性,因此其效率较低,对高维数据集的维度可扩展性差,无法适应于海量高维数据;Keller等人[19]利用蒙特卡洛方法寻找相关子空间集,该方法由数据对象对应在每个相关子空间中的局部数据子集确定该数据对象的离群程度,但该相关子空间实际上是从全局的角度考虑得到的;Sathe S等人[20]利用随机哈希的方法,提出了一种有效的子空间的离群检测方法,该方法能够大大降低时间复杂度,对海量的数据有着很好的适用性,但该方法不适用于挖掘局部的离群数据;张继福等人[9,22,23]利用局部稀疏差异因子,通过预先设定好的阈值对每个维度上稀疏因子进行区分,从而确定各数据对象的子空间定义向量,得到数据对象对应的相关子空间,解决了检测相关子空间时,时间复杂度较高的问题,一定程度上提高了算法的效率,但是,由于得到相关子空间时,是通过同一个阈值对所有的维度确定子空间,当各个维度的数据分布有差异时,得到的相关子空间有一定的误差.
综上所述,当数据对象分布不一致时,在检测到的相关子空间中,离群程度的度量不明显;在确定相关子空间时,具有维度指数级的时间复杂性;当参数阈值选择不合适的时候,精度无法保证,限制了算法的适用性.因此,其挖掘的效率和准确性也无法得到保证.
3 基本概念
在数据集中,分布集中或密度差异小的子空间称之为稠密子空间,分布稀疏或密度差异大的子空间称之为稀疏子空间.离群数据与正常数据的密度存在差异,离群数据是密度差异比较大的数据对象,密度差异较大的子空间,即稀疏子空间中包含有出比较多的对离群数据有价值的信息,而密度差异比较小的子空间,即稠密子空间中对离群数据有价值的信息比较少,因此将能体现更多对离群数据有价值信息的稀疏子空间称之为相关子空间,将体现较少对离群数据有价值信息的稠密子空间称之为不相关子空间.
在文献[9]中,为了寻找对离群数据有价值信息的稀疏子空间,利用数据对象的局部数据集LDS来计算第i条数据第j维度的数据稀疏度:
(1)
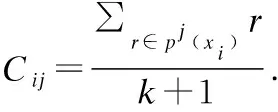
由公式(1)可知,yij是局部数据各属性维的方差,yij较大,表明xij在其局部数据集中的密度较小,xij所在的是稀疏子空间;反之,yij较小,表明xij在其局部数据集中的密度较大,xij所在的是稠密子空间.
稀疏度的引入,是可以更方便衡量数据空间的稠密和稀疏区域,发现数据空间的相关子空间.COAS算法[9]中使用局部稀疏差异因子阈值,来判断数据的相关子空间,但是,由于每个维度的数据分布特征不一致,这样会导致确定的相关子空间不准确.
4 相关子空间和离群值
4.1 相关子空间
依据文献[21],如果子空间S是稀疏子空间,则S是相关子空间;如果子空间S是稠密子空间,则S是不相关子空间.因此,可以通过识别子空间S中每个维度的稠密子空间和稀疏子空间,来确定出相关子空间.稀疏度矩阵每个维度的稀疏度yij是由稀疏子空间和稠密子空间混合组成的,而高斯混合模型的灵活性使其能够很好地适应稀疏度的分布,因此,通过高斯混合模型和EM算法识别稀疏度yij所在的子空间,可以得到该维度的稀疏子空间和稠密子空间,将其稀疏子空间视为相关子空间.
把一维数据对象xi稀疏度yij用作高斯混合模型:
(2)
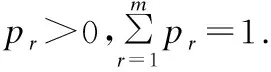
第r个高斯分布的密度函数为:
(3)
其中:每个部分的Nr含有两个参数期望μr和标准差σr,μr是高斯分布的位置参数,描述正态分布的集中趋势位置,分布以μr为对称轴,左右完全对称.σr描述正态分布资料数据分布的离散程度,σr越大,数据分布越分散,σr越小,数据分布越集中,σr也称为是正态分布的形状参数,σr越大,曲线越扁平,反之,σr越小,曲线越瘦高.
使用高斯混合模型对每一维度稀疏度进行拟合,把稀疏度分为两个高斯分布,稀疏度较大的分布中的数据构成相关子空间,较小的分布中的数据构成无关子空间,因此该高斯混合模型由两个高斯分布组成,即m=2.
使用EM算法来估计高斯混合模型各个参数[10],算法思想为:1)初始化:r1=r2=0,σ1=σ2=1,μ1、μ2为随机数;2)E步,计算后验概率;3)M步,根据后验概率计算新的r1、r2、μ1、μ2、σ1、σ2;4)判断是否结束,如果没有,返回2).
通过EM算法便可以得到每一维度的每个稀疏度属于两个高斯分布的概率值pi1和pi2,即可得到每一维度的每个数据对象稀疏度的高斯分布种类:当pi1>pi2时,该稀疏度属于第一个高斯分布;否则属于第二个高斯分布.同时可以得到每一维度的两个高斯分布的均值μ1、μ2,当μ1>μ2时,第一个高斯分布的稀疏度比较大,构成的子空间是稀疏子空间,第二个高斯分布的稀疏度比较小,构成的区域是稠密子空间,否则,相反.
定义:对于数据对象xi,yij是第i个数据对象第j维度的稀疏度,zi是其子空间向量,zij是第i个数据对象第j维度的值,如果yij属于稀疏子空间,则zij=1,如果yij属于稠密稠密子空间,则zij=0.在zi中,由值为1的属性维组成的空间称之为第i个数据的相关子空间,由值为0的属性维组成的空间称之为第i个数据的不相关子空间.
因此,利用稀疏度和上面的定义可以得到数据集各个数据对象的子空间向量.
COAS算法中子空间是根据其局部数据集是否均匀来判断的,而在实际数据中均匀分布是极为罕见的,因此采用均匀分布来判断相关子空间有一定的局限性.同时,在选择阈值时,COAS算法在不同维度选择同一个阈值进行相关子空间向量的计算,而在实际情况中每个维度的数据分布情况不完全相同.本算法避免用户设置的阈值参数,采用的混合高斯分布的方法可以自适应地识别每个维度的相关子空间.
4.2 离群值
根据相关子空间的定义,可以得到第i个数据对象的相关子空间,而稀疏度可以表示子空间的密度,离群程度越高,稀疏度越大,子空间的密度越小.因此,在相关子空间中,利用数据对象每个维度的稀疏度和每个维度的权值,可以有效地衡量数据对象的离群程度.
参照文献[8],数据对象i的离群值定义为:
(4)
即每个数据对象的离群值是该对象每个维度的离群程度之和,数据对象的离群值越高,其离群程度越大.数据对象i第j维的离群程度为:
(5)
其中,wj是每个维度在整个维度中的权值.
(6)
COAS算法中离群分数是把每个维度同等看待,并没有考虑到每个维度在数据空间中的重要性,本算法加入了权值因子能准确地区分每个数据对象的离群值.
5 RSGMM算法描述
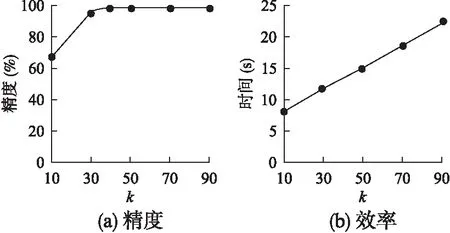
利用高斯混合分布模型确定相关子空间,并计算数据对象的离群值基本步骤:首先,生成数据集中每个数据对象的局部数据集LDS,然后根据公式(1)计算每个数据对象的稀疏度,生成全局地稀疏度矩阵;其次,利用混合分布和EM算法,确定每个数据对象的相关子空间;然后利用得到的相关子空间,根据公式(4)、(5)和(6)计算每个数据对象的离群值;最后选取离群值最高的若干个各数据对象,并将其视为离群数据.具体算法如下:
算法1.RSGMM算法
输入:数据集DS
输出:离群数据
1)n=数据集DS的数据个数,d=数据集DS的维度;
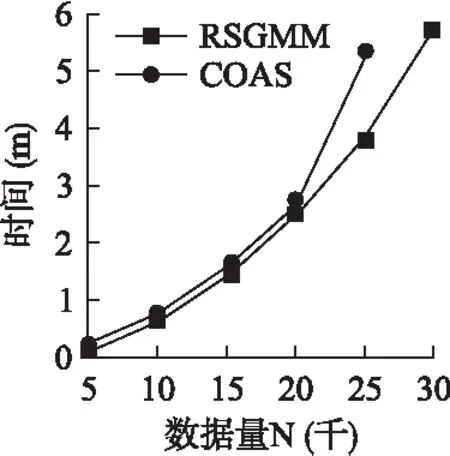
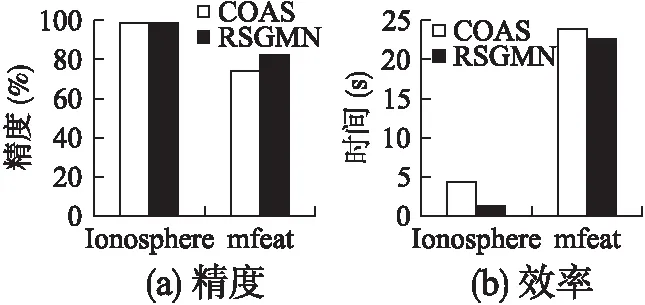
2)for(i=0;i 3)LDSi=getknn();//计算第i个数据对象的局部数据集LDS 4)spi=getspdegree();//计算第i个数据对象的稀疏度 5)} 6)Z=getsubspace();//计算相关子空间 7)for(i=0;i 8)Ri=getscore();//计算第i个数据对象的离群值 9)} 10)返回离群值最大的N个对象; 算法2.getspdegree() 输入:数据集DS,第i条数据对象的局部数据集LDS 输出:第i条数据对象的稀疏度 1)for(j=0;j 2)for(m=0;m 3)ine=line+LDS[m][d]; 4)} 5)pij=getsp(line);//根据公式(1)计算稀疏度 6)} 算法3.getsubspace() 输入:稀疏度矩阵sp 输出:二进制矩阵Z 1)for(j=0;j 2)根据EM思想进行迭代,得到Pik(k=0,1);//Pi为数据对象第j维属性属于第k类的概率 3)选择概率较大的类作为该属性的类别k(k=0,1); 4)for(i=0;i 5)选择均值较大的类别m(m=0,1); 6)if(m==k) 7)Zij=1; 8)else 9)Zij=0; 10)}} 算法4.getscore() 输入:稀疏度矩阵sp,二进制矩阵Z 输出:第i个数据对象的离群值Ri 1)for(j=1;j<=d;j++){ 2)根据公式(6)计算wj;//计算每个属性的权值 3)} 4)for(j=1;j<=d;j++){ 5)根据公式(4)计算离群值Ri;//计算第i 个数据对象的离群值Ri 6)} RSGMM算法中,计算各数据对象的局部数据集时,时间复杂度为O(n*logn),求每个数据对象求各属性的局部稀疏因子,生成原数据的稀疏因子矩阵时,其时间复杂度为O(n*k*d),识别相关子空间和确定离群值部分的时间复杂度是O(n*d)+O(d*t)+O(n*d)≈O(n*d),因此,RSGMM算法的时间复杂度是O(n*logn)+O(n*k*d)+ O(n*d). 实验环境:Intel(R)Core(TM)i5-3470CPU,2GB内存,windoes 7操作系统,eclipse 作为开发平台,采用 Java 语言实现了RSGMM算法. 生成50维、100维、150维、200维、250维和300维的5000条人工数据集;生成了50维的5000条、10000条、15000条、20000条、25000条和30000条人工数据集.在每条人工数据集中有3%的数据是离群数据,其中,正常数据由N(0,1)的正态分布生成的随机数,离群数据是由N(1,1)的正态分布生成的随机数. 1)参数k对RSGMM算法精度和效率的影响 采用数据量为5000条,维度为50维的人工数据集,对不同的k进行实验,实验结果如图1所示. 图1 k值对算法精度和效率的影响 由图1(a)可知,随着k值得增加,RSGMM算法的挖掘精度也将提高,主要原因是k值增大时,数据对象的局部数据集增多,使得数据对象的稀疏度增大,但是离群数据的稀疏度增大的幅度比正常数据明显,利用混合概率模型划分时,离群数据的所在的稀疏区域能更明显地识别出来,得到的相关子空间更加准确,其挖掘精度更高;当k>40时,算法的挖掘精度基本保持不变,其主要原因是:k值达到一定值时,数据的局部数据集可以体现其特征结构. 由图1(b)可知,近邻个数k对算法的挖掘效率影响比较大.随着k值得增大,其挖掘效率降低,主要原因是RSGMM算法大约70%多的时间用来计算稀疏度,且计算稀疏度时需要寻找k近邻,k值的越大,寻找k个最近邻的计算量也会随之增多. 2)维度对挖掘精度、效率的影响 采用数据量为5000条,维度分别为50维、100维、150维、200维、250维和300维的人工数据集,在参数k=40时对不同的维度进行实验,实验结果如图2所示. 图2 维度对算法的影响 在图2(a)中,维度对该RSGMM算法和COAS算法的挖掘精度都影响较低,其挖掘精度基本保持不变,主要是RSGMM算法在计算离群值前,首先进行了相关子空间的识别,排除了无关子空间对挖掘精度的影响,维度变化,对相关子空间维度影响不是太大. 但是,COAS算法比RSGMM算法的挖掘精度低,主要原因:1)在识别子空间的时候,COAS采用的是同一个阈值对所有维度进行区分,而在实际情况中每个维度的数据分布情况不完全相同,RSGMM算法采用混合分布的方法自适应对每个维度的数据进行区分,得到的相关子空间准确率比较高;2)COAS算法中离群分数是把每个维度同等看待,并没有考虑到每个维度在数据空间中的重要性,RSGMM算法加入了权值因子,能更好地区分每个数据的离群值. 在图2(b)中,RSGMM算法和COAS算法耗时随着维度的增加而线性增加,主要原因:1)RSGMM算法中,与维度相关的步骤稀疏度计算(公式(1))、确定相关子空间识和离群分数时的计算(公式(3)和(4)),都与维度是线性关系;2)COAS算法中,计算稀疏因子、稀疏差异因子、离群因子时,计算量都与维度d呈线性关系. 但是,RSGMM算法耗时比COAS算法要少,与图1的原因一致,RSGMM算法比COAS算法得到的相关子空间更加准确,得到的相关子空间维度更小,使得RSGMM算法在相关子空间中离群因子的计算量更小,算法消耗的时间更少. 3)数据量对算法挖掘效率的影响 图3 数据量对算法效率的影响 采用数据量分别为5000条、10000条、15000条、20000条、25000条和30000条,维度为50维的人工数据集,在参数k=40时对不同的数据量进行实验,实验结果如图3所示.图3中,RSGMM算法和COAS算法所消耗的时间都随着数据量的增加而增加,主要是由于随着数据量的增加,计算每个数据数据KNN、稀疏度、离群值的时间也会随着增加. RSGMM算法比COAS算法所消耗的时间少,原因与图2一样,RSGMM算法得到的相关子空间维度比较小,使得在较小维度的相关子空间中计算离群因子时,所消耗的时间大大降低,并且数据量越大,时间差距也越大,当数据量大于30000时,执行COAS算法所需要的内存超出了计算机的承受范围. 使用UCI数据集Ionosphere和mfeat,实验验证算法的精度和效率,表1为UCI数据集的组成. 表1 UCI数据集 在图4(a)中,数据集Ionosphere中,RSGMM算法和COAS算法的精度都是100%.数据集mfeat中,RSGMM算法比COAS算法中的精度要高,这是由于COAS算法得到相关子空间的是依据数据对象在其局部数据集中分布是否均匀来判断的,均匀分布的要求比较严格,得到的相关子空间包含了一些不相关的维度,隐藏在不相关的维度中的有些离群数据无法找到,而RSGMM算法可以发现影响大部分隐藏数据的相关子空间. 图4 UCI数据集对算法效率的影响 图4(b)中,在数据集Ionosphere和mfeat中,RSGMM算法比COAS算法消耗的时间要少,主要原因是RSGMM算法得到的相关子空间维度更小,使得在相关子空间中计算离群值时,消耗的时间更少. 本文针对高维离群数据,给出了一种基于相关子空间的离群数据挖掘算法.该算法利用各个数据对象各属性维的稀疏度(可以体现数据的稠密与稀疏)和高斯混合分布,确定各个数据对象的相关子空间和不相关子空间,有效地避免不相关子空间对挖掘精度和效率的影响;在相关子空间中,利用各个数据的稀疏度和各个属性维的权值来度量数据对象离群值,可以准确地度量数据对象的离群值;然后,将离群值最大的若干个数据对象视为离群数据;最后,采用人工数据集和UCI数据集实验验证了该算法正确性和有效性.下一步的工作是算法的并行化,以适应于海量高维数据.6 实验结果及分析
6.1 人工数据集

6.2 UCI数据集

7 结束语
