面向进化算法的问题相对求解难度降低方法
2018-11-15许春蕾昊1易鑫睿
许春蕾,陈 昊1,,易鑫睿
1(南昌航空大学 无损检测技术教育部重点实验室,南昌 330063 2(南昌航空大学 信息工程学院,南昌 330063)
1 引 言
进化算法是一类模拟进化机制的智能计算方法,其中提高算法求解能力与降低问题求解难度是进化算法有效求解优化问题的两个主要途径,由NFL定理[1]可知,不存在能够解决任何优化问题的超级优化算法,但是降低优化问题求解难度对于任何进化算法的研究都具有正面的指导意义.优化问题困难度是指通过较小的计算代价获得问题的信息,并以所得信息调节进化算法的控制参数[2,3],目前研究优化问题难度的方法和指标主要包括以下几个方面:
通过分析不同可行解间的距离和适应值的相互关系度量问题难度,包括适应值距离测试方法、关联长度测试方法等.Vanneschi等[4]在基因型之间定义一系列距离,选择其中一种距离计算适应值相关系数分析问题难度;Draskoczy[5]设计一种邻域算子计算搜索空间中可行解间的距离,分析不同距离间的特征和差异测试难度;Consoli等[6]通过分析显著性、相关性及上位性等问题特征描述问题难度,并将特征量化分类确定其对优化过程的影响.
通过对可行解空间进行子集划分度量问题难度,侧重于优化算法与问题之间的作用过程,包括最优吸引子理论、曲面自动机等.Chen等[7]将优化问题求解过程描述为探索与利用,利用采样点之间的信息相关性分析探索与利用作用过程;Rowe等[8]运用马尔科夫模型建立一种突变算子,分析不同等级适应度之间的转移概率,用曲面自动机精确建模.Munoz等[9]基于算法与优化问题之间的相互关系,研究一种基于信息特征的适应值曲面.通过适应值曲面的崎岖程度度量问题难度,主要运用关联长度测试方法.Malan等[10]在适应值曲面上构造随机游走序列,通过分析这个序列的自相关系数,描述优化问题难度;Shirakawa等[11]提出一个新的特征向量表征适应值曲面;Cai等[12]利用适应值曲面分析技术研究资源项目调度问题的难度.
除上述3种度量优化问题难度方法以外,还有一些其它的研究问题难度的方法,如基于信息论的基因关联度量方法[13],经典基因关联模型[14]、对问题分解重组[15]等.Gibbs等[16]定义决策变量之间的不平衡特性和相关性,并用具体的公式进行表示.Lu等[17]基于复杂度理论进行异位显性分析,提出改进的适应值曲面分解方法,对孤立点、单峰、多峰等不同适应值曲面的细节特征详细分析,并应用于参数调整的机器学习算法.
上述研究表明,有效辨识优化问题的求解难度对提高进化算法求解效率具有重要意义,但是目前关于问题难度研究还存在诸多缺陷,如适应值距离测试方法依赖于评价集的选取,最优吸引子理论仍没有合适的方法估算优化特征因子,现有的研究关于问题求解难度的度量方法主要停留在理论分析阶段且无法直接作用于进化过程,即问题求解难度在进化过程中无任何降低.本文提出一种面向进化算法的问题相对求解难度降低方法,以降低问题求解难度为目的,建立基于问题难度分析的相似性理论,对问题的简化表达式、最简表达式、相似性进行定义,利用基于云模型的相似性理论将问题估计为难度更低的相似问题.
2 难度分析方法
2.1 适应值距离测试方法
适应值距离测试方法(Fitness Distance Correlation,FDC)以评价集P的适应值和距离之间的相关系数描述优化问题[4].适应值距离相关系数FDCP可用公式表示为:
(1)


图1 FDC方法2种典型情况
2.2 适应值距离测试方法
关联长度测试方法(Correlation Length,CL)通过构造随机游走函数产生游走序列f(xt)描述适应值曲面的崎岖程度[10],先给定初值x0,再计算随机游走序列的自相关系数,根据自相关系数衡量优化问题难度.随机游走序列自相关系数R(l)可用公式表示为:
(2)

2.3 最优吸引子理论
最优吸引子理论(Optimal Contraction Theorem,OCT)以探索与利用平衡原理为基准[7],通过严格最优比(Strict Optimal Ratio,SOR)来对问题的难度进行分析,SOR是指最优区域(Optimal Field,OF)占整个搜索空间的比例,可用公式表示为:
(3)
式(3)中,SOR取值范围为(0,1],取值越趋向于1问题越简单,反之则越困难.
3 优化问题相似性
将优化问题的全局最优解定义为特征值,在问题特征值不变的前提下,对问题适应值曲面[18]的的任意变化都视作为对优化问题的一次问题变换,变换前后的问题具有不同的求解难度.根据本文2.3的最优吸引子理论可知,图2中F1、F2、F3的最优区域依次增加,F3的严格最优比等于1,难度最低.相似优化问题如图2所示.

图2 相似优化问题
根据最优吸引子理论可知新问题的难度低于原问题,则新问题是原问题的简化.本文认为新问题y=g(x)与原问题y=f(x)在问题变换前后是相似的.下面给出优化问题相似性的2个定义.
定义1.简化表达式、最简表达式若y=g(x)的最优区域OFg大于y=f(x)的最优区域OFf,由OCT可知,原问题经有限次问题变换后满足严格最优比为1,则将变换后的问题定义为原问题的简化表达式.简化表达式不唯一,定义其中与原问题y=f(x)差异最小的y=g(x)为原问题的最简表达式.若y=g(x)为y=f(x)的最简表达式,则应满足如下条件:
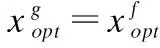
②OFf≤OFg
③ 对于∀xt∈X,满足f(xt)≤g(xt)
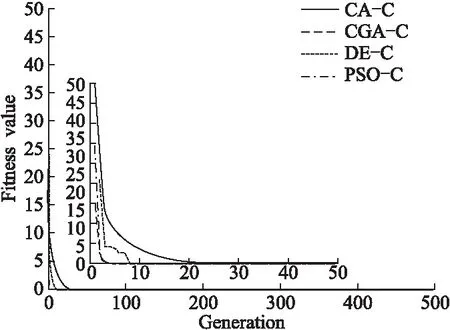
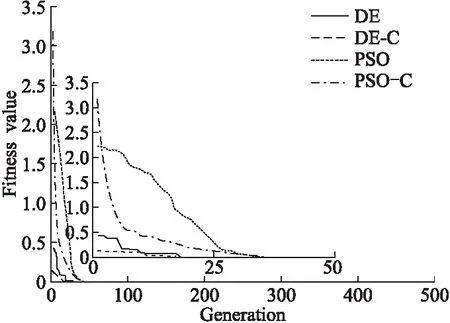
定义2.相似性若问题变换前后的优化问题具有相同的最简表达式,则称新问题与原问题是相似的.对于任意数值优化问题y=f(x),依据OCT,y=f(x)的严格最优比为SORf,若变换后的优化问题y=g(x)的严格最优比SORg≥SORf,则此变换为有效问题变换,变换后的优化问题难度小于原问题;若SORg 优化问题间的差异难以衡量,本文用固定数学形式的表示简化表达式,将简化表达式y=g(x)表示为云模型C(Ex,En,He): (4) 式(4)中,Ex表示期望,对应C的中心点;En表示C的熵,根据3En准则可确定C的作用范围;超熵He与C的置信度成反比. 若构建的云模型满足定义1中最简表达式的3个条件,则C(Ex,En,He)为y=f(x)最简表达式的云模型表示,即最简云模型Cbest(Ex,En,He).本文将进化算法的搜索目的扩展为寻找优化问题对应的最简云模型,在t代对最简云模型进行估计,寻找以当前最优解xopt(t)为中心点的云模型C(t),且C(t)尽可能满足最简表达式的条件③,将寻找的最简云模型过程可归纳为一个优化问题,用数学模型描述为: (5) 式(5)中,R表示规模固定的样本集;D表示评价最简云模型与原问题函数值差异的距离函数.由进化过程中估计的最简云模型可引出如下定理. 定理:进化过程中估计的最简云模型Cbest(Ex,En,He)与原优化问题y=f(x)前后相似. 证毕. 4.2.1 相似性理论对问题相对求解难度的影响 对于某一特定的优化问题,其真实的求解难度是不变的,如利用最优吸引子理论分析问题求解难度时,是以已知问题全局最优解为前提的,无法在进化过程之中进行测度.本文提出相对求解难度(Relative Solution Difficulty,RSD)的概念. 定义3.相对求解难度在利用进化算法求解问题之前,问题的真实难度与相对难度均是未知的;已知问题最优解xopt时,可建立Cbest(Ex,En,He),问题的真实难度未改变,可用3个难度衡量指标求出其相对求解难度;在进化过程之中,随着优良解的不断产生,相对求解难度在逐渐下降. 优化问题相对求解难度变化示意图如图3所示. 图3 优化问题相对求解难度变化示意图 在进化过程中的第t代所估计的最简云模型为C(t)=(Ex(t),En(t),He(t)),则可将原优化问题可变换为: y=max(f(x),gC(x)) (6) 由相似性理论可知,估计的新问题不改变问题的全局最优解,且新问题具有更低的相对求解难度.由图2可知,估计的F2和F3比原问题F1难度更低,其中已估计为单峰函数的F3的严格最优比为1,即相对求解难度为0. 4.2.2 最简云模型求解方法 式(5)为已知云模型期望求解熵的优化问题,该问题出现在利用进化算法求解优化问题的过程之中.估计最简云模型的准确性直接影响问题的相对求解难度,本文先确定熵的取值范围并生成种群,在搜索域内随机采样构造样本集,以样本集内采样点处云模型与原问题的距离对熵个体进行评价.求解熵值具体伪代码如下所示: begin 设t为进化代数,初始化种群Ent 构造评价集R repeat for每一个个体Qi endfor Ent+1=select(Ent,D)//根据个体适应值选择一定数量的个体 Ent+1=newcrossover(Ent+1,recdis)//交叉产生新子代,recdis为交叉函数 Ent+1=mutate(Ent+1,mutbga)//子代进行变异操作,mutbga为变异函数 untilterminated=ture end 4.2.3 进化算法与最简云模型结合 对于一个优化问题,将进化算法与问题相对求解难度降低方法相结合,可有效降低问题相对求解难度.原有进化算法中,从进化开始至进化结束,问题相对求解难度无任何变化,问题的难度始终在同一个层次上,而本文在进化算法的基础上引入问题难度降低方法,可在进化过程中建立与优化问题对应的最简云模型,能有效降低问题相对求解难度,基于最简云模型的进化算法具体实现步骤如下: Step1.t=0,产生初始化种群Pt. Step2. 在种群中找出当前最优个体作为最简云模型的期望值. Step3. 利用4.2.2节方法求得最简云模型的熵值. Step4. 由Step 2和Step 3确定最简云模C(t). Step5. 根据第2节种难度分析方法求当前问题的相对求解难度. Step6. 计算个体适应值. Step6.1. 种群实际适应值y1=f(Pt). Step6.2. 种群在最简云模型上的值y2=gc(Pt). Step6.3. 个体适应值fitness(Pt)=max(y1,y2). Step7. 利用个体适应值进行选择、交叉、变异操作. Step8. 得到新种群Pt+1. Step9. 终止条件判断.若t>tmax,算法结束并输出结果,否则跳转到Step 2. 本文将选取7种测试函数,在文化算法(Cultural Algorithm,CA)、差分进化算法(Differential Evolution,DE)、元胞遗传算法(Celluar Genetic Algorithm,CGA)和粒子群算法(Particle Swarm Optimization,PSO)的基础上引入本文方法,即CA-C、DE-C CGA-C、PSO-C.每个算法独立运行30次,进化代数均设置为500代,种群规模都设置为200,测试函数对照表如表1所示. 表1 测试函数对照表 函数相对求解难度测试实验结果如表2所示,算法在2维对各函数运用第2节介绍的3种方法对问题相对求解难度进行测试.其中1st、10th与50th分别为测试函数的真实求解难度、函数运行到第10代与第50代的相对求解难度;R表示函数的最终求解难度;Ave为函数在运行过程中的平均相对求解难度,即30次求解难度结果的平均值;数据加粗表示问题平均相对求解难度与真实难度相比具有显著差异;“*”表示问题平均相对求解难度与真实难度相比具有极显著差异.显著性分析采用T检验方法,显著性水平设置为0.05. 表2 函数相对求解难度测试实验结果 分析表2数据可以发现:4种算法引入本文方法后,问题相对求解难度均有明显降低.F1为简单单峰函数,4种算法由FDC测得的初始难度均在0.9附近,由平均相对求解难度数据可知问题求解难度有一定程度降低;4种算法利用CL求得的问题相对求解难度较接近,CA-C难度降低幅度最大,幅度降低最小的是CGA-C;因F1是单峰函数,所以OCT测得的问题真实难度均相同.针对F2函数,根据FDC所得的问题真实求解难度,DE-C求得的真实难度最高,CGA-C求得的真实难度最低;利用CL求得的F2函数真实难度,CA-C的问题真实难度最低,仅为0.01,且从真实难度到最终相对难度数值降低89.6倍;各算法利用OCT测得的问题真实难度为0.08.FDC和CL对F3函数的问题求解难度影响不大,而OCT对降低难度十分有效,4种算法由OCT求得真实难度为0.09,问题最终相对求解难度均降低为1.针对线性不可分F4函数,PSO-C利用FDC在第10代求解的问题相对难度为0.79,相对于真实难度0.01,难度降低79倍,说明问题相对求解难度降低方法在进化初期已有明显作用.F5为多密集尖峰函数,4种算法利用OCT测得问题平均相对求解难度与真实求解难度对比差异极显著,DE-C降低8.9倍,幅度最小,CGA-C降低11.5倍,幅度最大,所以基本进化算法引入本文难度降低方法,在解决多峰问题时具有显著优势.针对复杂多模态F6函数,PSO-C利用FDC测得的问题求解难度变化不大,仅为5.7%;DE-C和CGA-C利用OCT测得的问题平均相对难度与真实难度相比差异极显著. 通过分析比较测试结果可以发现,4种算法加上本文方法后,在运行中问题的相对求解难度依次呈现递减的趋势.整体来看,除了简单单峰函数F1之外,CA-C、DE-C、CGA-C和PSO-C算法对每个测试函数都取得了较好的测试效果,说明面向进化算法的问题相对求解难度降低方法具有较好的问题相对求解难度降低性能,且具有较强的稳定性和通用性. 为了验证本文方法对不同进化算法寻优性能的影响,又分别利用CA-C、DE-C、CGA-C和PSO-C算法对F2、F4和F5函数进行测试(所有参数设置保持不变),最终得到如图4和图5所示的测试结果. 图4 F2函数适应值变化曲线 对于F2函数,通过适应值变化曲线可以看出,CA-C、DE-C、CGA-C和PSO-C算法均能在100代之内寻找到最优解,其中DE-C算法在进化初期就发现最优解,其次效果较好的是PSO-C算法,说明DE-C算法具有较高的收敛性能.在复杂多峰的F5函数测试中,4种算法都在30代之内达到全局收敛,CGA-C和PSO-C算法收敛速度相当,说明基本算法引入本文方法后,能较快且准确的搜索到最优解. 图5 F5函数适应值变化曲线 为了更好的说明优化问题相对求解难度降低方法对不同算法寻优性能的影响,测试了CA、DE、CGA和PSO算法在引入本文方法前后各函数的最优适应值变化情况,图6和图7为CA和CGA算法前后对比图,图8和图9为DE和PSO算法前后对比图. 图6 CA和CGA对于F3函数测试结果对比 图7 CA和CGA对于F6函数测试结果对比 由图6-图9可以发现,针对不同算法对于不同问题,是否采用本文优化问题相对求解难度降低方法取得的效果并不一致.图6中,对F3函数测试时,随着进化代数增加,4种情况都能达到全局收敛,但CA-C和CGA-C算法较CA和CGA具有更快的收敛速度,同等条件下,F6函数取得的测试结果基本与F3函数一致,由图7的适应值迭代曲线可明显看出.图8对比了DE和PSO算法采用本文方法前后的测试结果,由DE-C和PSO-C的测试曲线可以看出,其收敛代数比DE和PSO收敛代数少,且在25代内搜索到全局最优解,从图9可看出,F6函数曲线变化趋势基本与F3函数一致. 图8 DE和PSO对于F3函数测试结果对比 图9 DE和PSO对于F6函数测试结果对比 通过以上实验测试结果可以看出,CA、DE、CGA和PSO这4种基本算法引入本文方法,能够有效降低问题相对求解难度,且CA-C、DE-C、CGA-C和P`SO-C算法相比原来的基础进化算法具有更好的全局收敛效果,使全局收敛速度有很大提升. 本文提出了一种面向进化算法的问题相对求解难度降低方法.首先介绍了3种衡量优化问题求解难度的方法,然后对优化问题相似性进行理论分析,将基于云模型的相似性理论引入到进化过程当中,并分析相似性理论对问题相对求解难度的影响.最后分别在4种传统进化算法上引入本文提出的方法,利用3种指标对进化过程中的问题相对求解难度进行测试,以及验证本文方法对不同进化算法寻优性能的影响.从试验结果可以看出,4种基本算法加上本文问题难度降低方法后,由进化过程中不同阶段的问题相对求解难度数据可知,不同难度指标测试所得的相对求解难度依次呈现递减的趋势,且对每个测试函数都取得了不错的测试效果,说明方法具有较强的稳定性和通用性.同时,本文方法对算法的寻优性能也有着积极的影响,传统进化算法引入本文方法之后能够更快更精确找到问题的全局最优解.4 基于相似性理论的问题相对求解难度降低方法
4.1 云估计
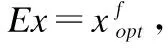
4.2 相似性理论对问题相对求解难度的影响及最简云模型求解方法


5 实验数据及分析

5.1 问题相对求解难度测试结果与分析

5.2 算法寻优性能测试结果与分析



6 结 论
