基于模型的液力变矩器故障诊断系统的设计与校验∗

陈 奇，姚志刚，陈无畏，Qadeer Ahmed，张 振

(1.合肥工业大学机械工程学院，合肥 230009； 2.俄亥俄州立大学汽车研究中心，哥伦布，美国 43212)

前言

进入新世纪以来，随着全球经济和科学信息技术的快速发展，当今世界汽车工业也步入了高速发展的阶段。液力式自动变速器(AT)作为汽车的核心零部件，由液力变矩器、行星齿轮、液压操纵系统和电子控制系统组成，通过液力的传递和行星齿轮机构组合的方式来达到变速变矩的目的，液力变矩器发生故障与否对于整车安全性和可靠性具有非常重要的影响。因此，进行液力变矩器故障诊断系统设计，监控其工作状态，保障其运行安全，具有重要意义。

目前，故障诊断的理论研究[1]已比较成熟，大致分为3类:基于解析模型的方法[2-4]、基于信号处理的方法[5-6]和基于知识的方法[7-9]。其中基于模型的故障诊断方法应用最为广泛[10]。然而，对于液力变矩器的故障诊断理论研究极少，赵瑞萍研究了防爆胶轮车用液力变矩器的主要故障表现形式[11]。其余有关液力变矩器故障诊断的文献大都集中在结构和电气等故障维修的实际工程应用[12-13]。为进行液力变矩器的故障诊断系统设计，本文中采用近年来国外学者提出的一种新型的故障诊断方法——结构分析法(structural analysis，SA)。其基础是基于模型的故障诊断理论，它不依赖于具体的参数，只取决于系统的结构模型，能快速地分析复杂系统中的故障可诊断性和可隔离性；其设计算法简单，可有效提高故障诊断效率，避免故障的误诊和漏诊，较好地满足液力变矩器的故障诊断需求。有关SA的研究成果主要有:Chen[14]等人以AMT为例，利用SA方法确定传感器最优布置方式，用以实现故障可检测性和可隔离性的最大化；Zhang[15]等人利用结构分析法，推导出一套用于故障检测和隔离的解析冗余关系式，用于电动汽车的故障诊断；Chen和Ahmed[14，16]等提出了基于SA的残差设计方法，并将该方法用于AMT换挡执行机构的故障诊断。

因此，为全面客观地评估液力变矩器关键故障的可检测性和可隔离性，并快速实现其故障诊断系统的设计，本文中引入基于结构分析法(SA)的故障诊断理论。通过研究液力变矩器可能存在的关键故障，并结合其系统模型，建立液力变矩器的故障模型；利用SA理论中的DM(dulmage-mendelsohn)分解和故障隔离矩阵(fault isolability matrix，FIM)技术对液力变矩器进行故障可检测性和隔离性分析；探讨结构最小型超定方程集(minimal structurally over-determined sets，MSO sets)的获取策略，并利用解析冗余关系式(analytical redundancy relations，ARR)和基于观测器参数评估的方法，设计具有稳定性的残差；在MATLAB/Simulink中建立故障检测与识别(fault detection and identification，FDI)系统仿真模型，并进行故障诊断模拟。将诊断结果与SA理论分析对比，验证基于结构分析法的故障诊断方法的可行性和有效性。

1 液力变矩器系统的关键故障分析

1.1 液力变矩器简介

液力变矩器是一种以自动变速器油(automatic transmission fluid，ATF)为工作介质的非刚性传动装置。它的主要功能为防止发动机过载和调节工作机构的转速与转矩。它位于自动变速器的最前端，安装在发动机飞轮上，利用油液循环流动过程中动能的变化将发动机动力传递给自动变速器。其结构主要由壳体(泵轮)、涡轮、导轮(带单向离合器)和锁止离合器组成，如图1所示。

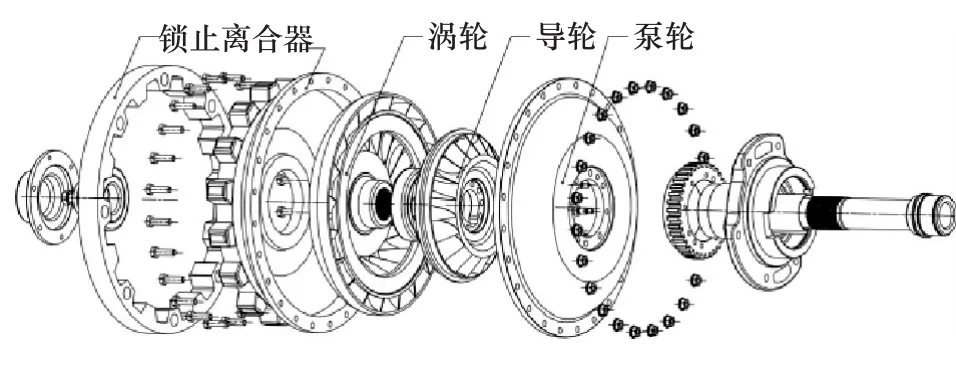
图1 液力变矩器的结构组成

1.2 液力变矩器系统的关联故障分析

由文献[11]和文献[13]可知，液力变矩器的故障主要表现为油温高、供油压力低、泄漏、车辆行驶速度低或无力和工作时内部出现异常响声。这些故障仅影响液力变矩器的传动效率，不会危及其运行安全。但其中泵轮和飞轮的可靠连接对液力变矩器至关重要，因为当其发生故障时，发动机的动力将不能传递到变速器，直接影响汽车的安全行驶，其危害性最大。

另外，与液力变矩器系统相关的4个传感器(涡轮转速、泵轮转速、车速和发动机转速传感器)对于液力变矩器运行状态的监测也很关键。因此，液力变矩器系统的关键故障及其可能存在的表征形式如表1所示。

表1 液力变矩器故障变量及其表征形式

本文中将重点对这些故障进行诊断与识别。

2 液力变矩器故障模型的建立

由作者前期对SA的研究[14，16]可知，在应用SA时，首先需要建立系统的故障模型，即将关键故障通过变量形式引入到系统模型中，建立含有故障参数的数学模型。本节将重点讨论液力变矩器故障模型的建立过程。

考虑到液力变矩器安装在发动机与变速器之间与发动机、变速器和车轮负载模块紧密相连，故其系统数学模型主要由发动机模型、液力变矩器模型、自动变速器、主减速器和负载模型组成。根据表1中的故障变量和表征形式，结合液力变矩器的系统数学模型，即可建立液力变矩器关键故障模型:

式中:Te为发动机输出转矩；Tb为泵轮输出转矩；Tt为涡轮输出转矩；Je为发动机(包括飞轮)的转动惯量；Jb为泵轮转动惯量；ωe为发动机角速度；ωb为变矩器泵轮角速度；ωt为变矩器涡轮角速度；v为汽车行驶速度；r为车轮半径；i为变矩器速比；K为变矩器变矩比(与i有关的系数)；m为汽车质量；f为车轮与地面的滚动摩擦因数；CD为空气阻力系数；A为汽车迎风面积；ρ为空气密度；vr为汽车与空气的相对速度；δ为汽车旋转质量换算系数；ig为变速器速比；i0为主减速器速比；yωt，yωb，yv和 yωe分别为各个传感器的测量值。

3 基于SA的故障可检测性(FD)和可隔离性分析(FI)

结构分析法(SA)是一种新型的故障诊断方法[17-18]，属于模型类的故障诊断方法。它利用图形工具，评估系统的故障可检测性和可隔离性，并可构建结构最小型超定方程集(MSO sets)，用于残差设计。本节重点讨论应用SA方法进行液力变矩器的故障可检测性和可隔离性分析。

3.1 系统结构表征图

系统结构表征图(structural representation)主要用于描述系统包含的所有变量与约束方程之间的对应关系，忽略变量与方程之间的具体数学关系，可用关联矩阵的形式表示。矩阵中行表示约束方程，列表示系统的未知变量、已知变量和故障变量。符号“×”在关联矩阵的位置为(i，j)，即表示约束方程ei与第j列的变量存在关联关系[19]。

由式(1)可得在液力变矩器故障模型中，系统方程集、已知变量集、未知变量集和故障变量集分别为

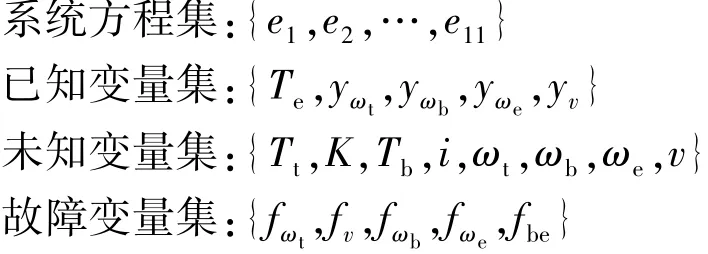
液力变矩器故障模型的结构表征图如图2所示。其中，“×”表示等式ei与对应的变量存在关联关系。

图2 液力变矩器故障模型的结构表征图

3.2 液力变矩器故障可检测性和可隔离性分析

(1)故障可检测性(FD)分析

故障可检测性(fault detectability，FD)指当系统中有故障发生时，能否检测到哪些故障发生。由文献[20]中定义知，如果方程中的故障f位于结构超定部分M+，即如式(2)所示的关系，则说明该故障f是可检测的。

根据上述对于故障可检测性定义，如果含有故障的方程位于结构超定部分M+，则故障是可检测的。图3给出了液力变矩器故障模型的DM分解图，结果显示所有的关键故障都位于结构超定部分M+。因此该模型经DM分解后，所有故障都可检测。

图3 液力变矩器故障模型的DM分解图

(2)故障可隔离性(FI)分析

故障可隔离性(fault isolability，FI)指当该故障发生时，能否将其从其他故障中隔离与定位。在一个系统模型M中，如果故障fi和fj满足式(3)的关系，则故障fi就能从故障fj中隔离出。

式中:efi为含有故障fi的方程；efj为含有故障fj的方程；(M/efj)+为消去方程efj的结构超定部分。

SA中的故障隔离矩阵(faultisolabilitymatrix，FIM)用于FI分析，它可直观地反映出各故障的可隔离性[21]。根据式(3)的原理，应用自编的SA分析程序，可得到液力变矩器的FIM矩阵，如图4所示。其中，“·”表示水平方向上的故障与竖直方向上故障之间的关联关系:若一个故障只存在自相关关系，此故障是可隔离的；若一个故障与其他故障存在关联关系，此故障是不可隔离的。由此可见，所有的故障都可隔离。

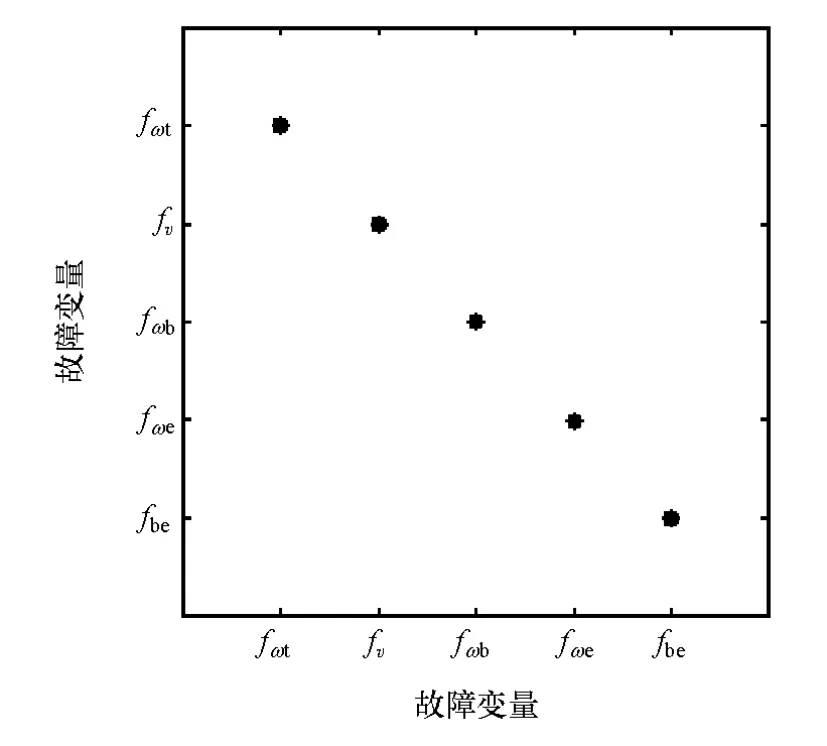
图4 液力变矩器故障模型的FIM矩阵

3.3 结构最小型超定方程集(MSO sets)

分析系统故障的可检测性和可隔离性之后，为了生成序列残差用以检测到特定的故障，可从DM分解图中的结构超定部分M+获得结构最小型超定方程集。在获取MSO集时，尽量避免积分和微分环节，从而可较容易地设计序列残差，并能保证其稳定性和鲁棒性。

根据文献[22]和文献[23]中的MSO求解策略，运用MATLAB工具箱，即可通过编程获得全部的MSO集。对于此液力变矩器故障模型，通过分析可得:其总共有5个MSO集(T1～T5)，每个MSO集所包含的方程如表2所示。

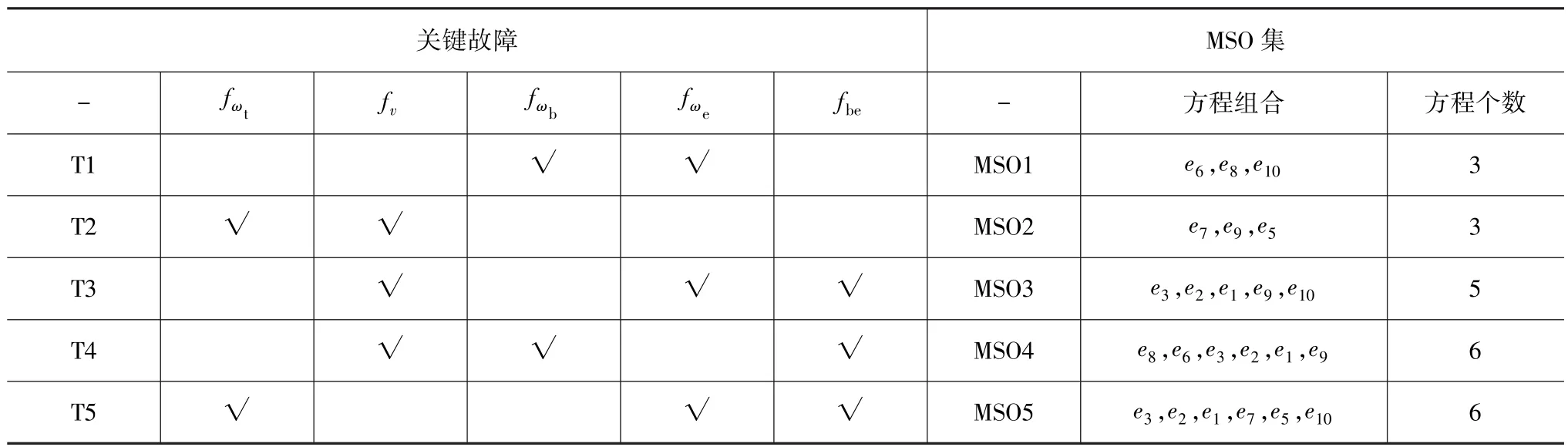
表2 液力变矩器故障模型的MSO集

其中，符号“√”表示故障是可检测的，空白处表示故障不能检测。 例如，T1能检测fωb和fωe故障，但是不能检测 fωt，fv和 fbe故障。

4 残差设计

在基于模型的故障诊断中，残差用于故障的检测和隔离，是FDI系统中重要的组成部分，通过对残差的分析判断，确定系统故障是否发生。本文中残差评价的主要方法是通过设定合适的报警阈值，然后将残差与报警阈值进行对比，如果残差超过了报警阈值，则发出故障警报，表明系统发生故障。

根据表2可知，液力变矩器系统共有6个MSO集，因此共可产生6个残差，分别设计如下。

(1)残差1 由表2可得，方程集MSO1由3个方程{e6，e8，e10}组成，由于泵轮转速和发动机转速测量方程包含在MSO1中，所以MSO1可用于检测到泵轮转速传感器故障fωb或发动机转速传感器故障fωe。理论上，MSO1中的每个方程都可生成残差，但须选择一个方程同时包括泵轮转速变量和发动机转速变量作为冗余方程，也就是方程e6。利用方程e6产生残差R1:

(2)残差2 由表2可得，方程集MSO2由3个方程{e7，e9，e5}组成，它可用于检测涡轮转速传感器故障fωb或车速传感器故障fv。同理可得，选择e5作为冗余方程产生残差R2:

(3)残差3 由表2可得，方程集MSO3由5个方程{e3，e2，e1，e9，e10}组成，由于方程 e2和 e1都含有微分项，可能会造成系统的不稳定，所以不能直接采用上述方法。利用方程e1产生一个解析冗余关系(ARR)[24]，并将方程 e3，e2，e9和 e10代入方程 e1中，得到如下形式:

引入一个新的状态变量x和参数β[25]，式(6)的新形式和残差的状态空间可表示为

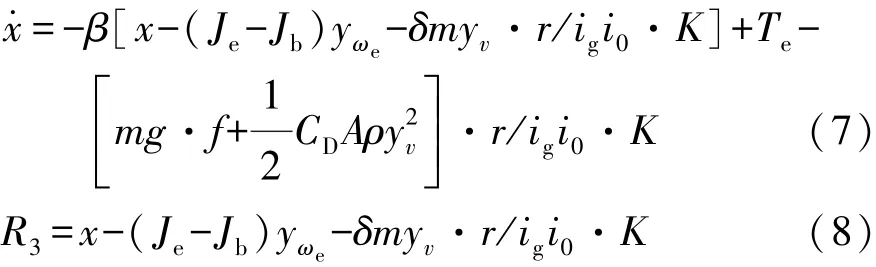
式中，根据文献[17]中的结论，β＞0用于保证系统的稳定性，＝ 0。

(4)残差4 由表2可得，方程集MSO4由6个方程{e8，e6，e3，e2，e1，e9}组成。 应用残差 3 的方法，同理可得残差R4。

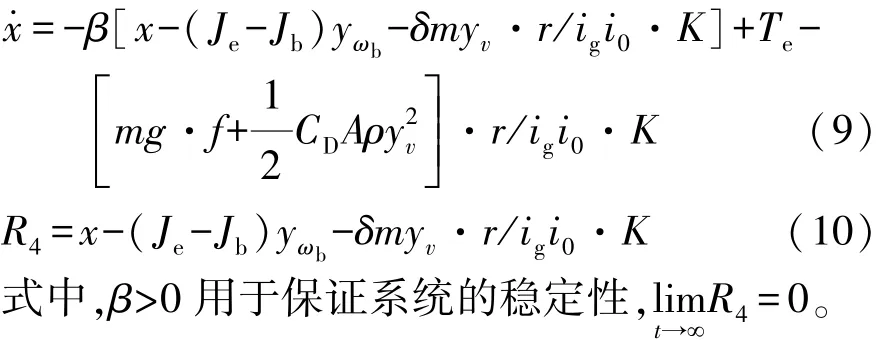
(5)残差5 由表2可得，方程集MSO5由6个方程{e3，e2，e1，e7，e5，e10}组成，由于方程 e2和 e1都含有微分项，可能会造成系统的不稳定，所以利用方程e2产生一个解析冗余关系(ARR)，并将方程e3，e1，e7，e5和 e10代入方程 e2中，得到如下形式:

5 FDI系统模型仿真与校验

5.1 FDI系统模型建立

为验证上述基于SA方法的故障可检测和可隔离分析结果的正确性，本节将利用上述5个序列残差进行FDI系统设计，并运用Simulink软件对其进行仿真与校验。

FDI系统的建模最重要的是序列残差模型的建立和故障信号的仿真。从建模和仿真的角度出发，故障信号的模拟类型如下:对于偏差故障，可在原信号上加上一个恒定或随机的小信号；对于增益故障，可在原信号上乘以一定的倍数；对于干扰故障，可在原信号上叠加一个白噪声信号；对于信号消失故障，可把原信号某一时间段内的信号设置为零。根据上述故障模型和残差设计公式，可在MATLAB中建立FDI系统Simulink仿真模型，如图5所示。

图5 FDI系统Simulink仿真模型

5.2 液力变矩器FDI系统仿真与校验

5.2.1 故障模拟

考虑到当前还不具备实车故障实验的条件，本文中采用仿真方法，通过在一定时间设置故障，检查FDI系统能否及时检测，并将结果与上述SA的分析对比。

根据上述故障信号的模拟类型的讨论，表3给出了液力变矩器故障种类、故障信号模拟类型和故障发生的时间。

表3 液力变矩器故障模拟

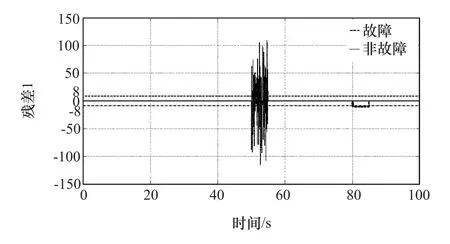
图6 残差R1信号输出响应

图7 残差R2信号输出响应

图8 残差R3信号输出响应

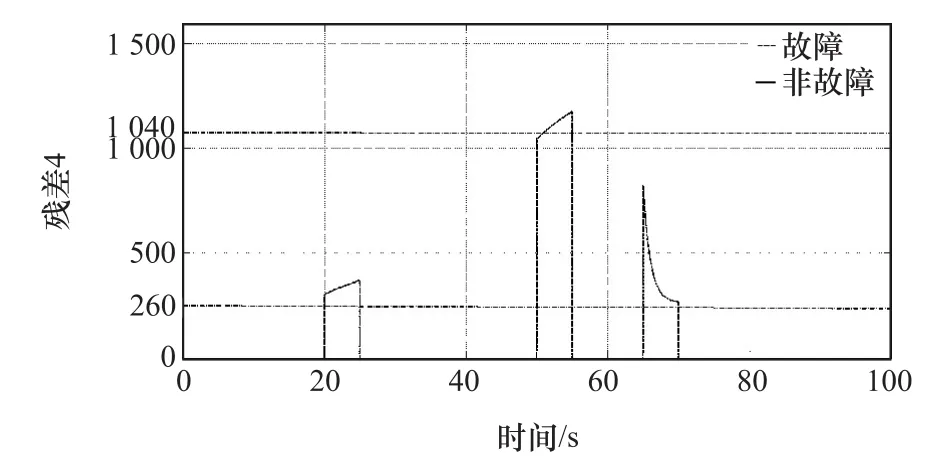
图9 残差R4信号输出响应

5.2.2 仿真验证

在预先设置故障后，对系统模型进行仿真，即可获得FDI系统中5个序列残差的信号输出情况，如图6～图10所示。为快速评估FDI系统，选择合适的固定值作为残差的阈值[26]，将残差的值是否超过对应的阈值作为是否发生故障的判断条件。

由图6～图10可知，残差R1在50和80s处可检测到故障，而在20，35和65s处不能检测到故障，即残差 R1可检测故障 fωb，fωe，不能检测故障 fbe，fωt和fv；残差R2在35和65s处可检测到故障，而在20，50和80s处不能检测到故障，即残差R2可检测故障fωt，fv，不能检测故障 fbe，fωb，fωe；残差 R3在 20，65 和80s处可检测到故障，而在35和50s处不能检测到故障，即残差 R3可检测故障 fbe，fv和 fωe，不能检测故障 fωt和 fωb；残差 R4在 20，50 和 65s 处可检测到故障，而在35和80s处不能检测到故障，即残差R4可检测故障 fbe，fωb和 fv，不能检测故障 fωt和 fωe；残差 R5在20，35和80s处可检测到故障，而在50和65s处不能检测到故障，即残差 R5可检测故障 fbe，fωt和 fωe，不能检测故障 fωb和 fv。

表4给出了上述5个残差检测故障的结果。

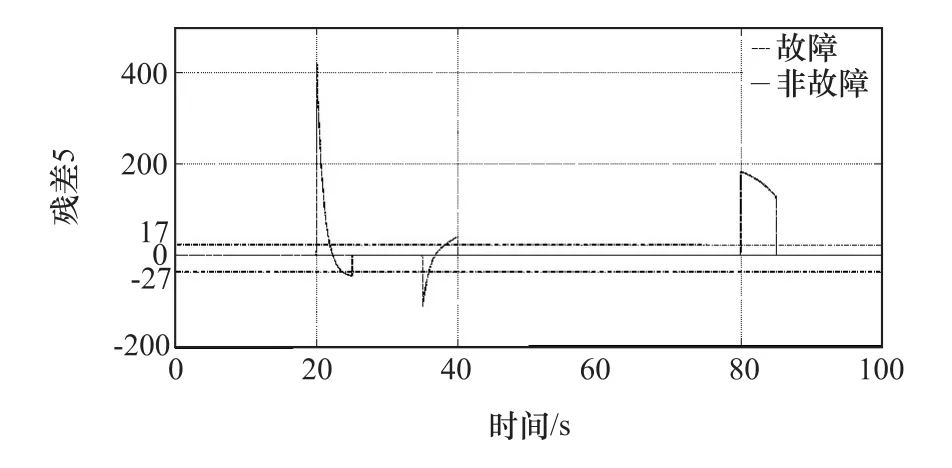
图10 残差R5信号输出响应

表4 液力变矩器故障残差的检测结果

由表4可见，FDI系统的故障检测结果与表2的分析结果一致，因此说明了基于结构分析法的故障诊断方法的可行性和有效性。

6 结论

(1)根据液力变矩器关键故障的特征，引入故障变量参数，建立了液力变矩器故障模型；运用基于结构分析法(SA)的故障诊断理论，利用结构表征图获得了液力变矩器故障模型的未知、已知和故障变量集；运用DM分解得到了液力变矩器关键故障的可检测性(FD)与可隔离性(FI)分析结果；使用DM分解获得了结构最小型超定方程集(MSO sets)，并通过基于解析冗余关系式(ARR)方法进行了残差设计。

(2)在MATLAB/Simulink环境下搭建了FDI系统仿真模型，将整车系统模型中的相关信号引入到FDI系统中，并预设故障；通过选择固定阈值的方法作为故障是否发生的判断条件，将仿真诊断结果与预先设置的故障进行对比，结果表明仿真结果与理论分析一致，证明了FDI系统的正确性和有效性，验证了基于结构分析法可用于液力变矩器的故障诊断和识别。