基于参考模型的复合功率分流系统模式切换中的转矩协调控制∗
2018-11-15赵治国蒋蓝星李蒙娜王茂垚
赵治国,蒋蓝星,李蒙娜,王茂垚
(同济大学新能源汽车工程中心,上海 201804)
前言
功率分流混合动力系统采用行星排机构将发动机和电机耦合起来,可实现速比的连续变化,并使发动机始终工作在其最佳工作点[1],已被广泛应用于混联式混合动力汽车。行星排功率分流方式可以划分为输入、输出和复合功率分流3种[2-3],此外,这3种功率分流方式可以叠加,从而构成多模式混合动力系统。为适应不同的工况,功率分流系统须频繁进行模式切换。然而,与传统的P0~P4构型相比,功率分流混合动力系统取消了液力变矩器或干摩擦离合器,系统的欠阻尼特征明显。所以,功率分流系统模式切换过程平顺性问题较为突出[4]。
目前已有很多学者对功率分流系统的模式切换问题进行了研究。文献[5]中对一种复合功率分流混合动力系统进行实车试验,结果表明在模式切换过程中车辆在纵向的加速度波动最大,并与系统转矩波动变化一致。在此基础上,以减小车辆纵向加速度波动为目标,设计了电机的补偿转矩。文献[6]和文献[7]中对通用双模AHS系统进行研究,使用电机动态补偿发动机起动过程所造成的系统转矩波动,并采用旁通式扭转减振器将发动机与变速器直接连接,进一步改善了模式切换的平顺性。文献[8]中研究了一种复合功率分流系统驱动模式切换过程,提出基于结构特点使用电机转矩来估计发动机转矩的方法,然后采用电机转矩补偿系统转矩波动。文献[9]中针对一种复合功率分流系统,使用基于实时非线性降维鲁棒观测器估计输出轴转矩,设计了主动阻尼控制策略,计算出两个电机的补偿转矩。然而,上述方法研究的切换过程均为纯电动至e-CVT模式切换,从使用电机转矩抵消系统波动的角度进行优化,没有考虑到建立模式切换评价指标冲击度与电机和发动机转矩之间的直接联系,通过目标冲击度计算系统转矩变化,将研究过程拓宽至纯电动和e-CVT混合动力模式之间的切换。
本文中以一种复合功率分流混合动力系统为研究对象,提出了一种基于参考模型的协调控制策略。针对该系统纯电动和e-CVT混合动力模式之间相互切换的过程进行分析,建立了模式切换过程的动态模型。然后设计转矩分配策略,使模式切换过程动力不中断。在此基础上,推导出冲击度参考模型,对两个电机转矩变化进行限制,以提高驾驶平顺性。仿真和试验结果表明,该策略能有效地降低冲击度。此外,所提出的协调控制策略不仅适用于本文的研究对象,也能应用于其他的双行星排构型,为功率分流混合动力系统模式切换策略的开发提供参考。
1 复合功率分流系统建模与分析
1.1 复合功率分流系统结构
文中所研究的双行星排复合功率分流系统如图1所示。其中,电机1(MG1)与前排小太阳轮S1相连,电机2(MG2)与后排大太阳轮S2相连,发动机(ENG)从前后排共用的行星架CR1输入动力,前后排共用齿圈R1与输出轴(OUT)相连。系统还包括两个制动器B1和B2,B1用来在纯电动模式锁止输入轴,B2用来在高速混合动力模式锁止小电机1,防止功率回流[10]。

图1 双行星排复合功率分流系统
该系统主要在以下3种模式工作:
(1)纯电动模式:制动器B1锁止、大电机2单独驱动车辆行驶;
(2)e-CVT混合动力模式:两个制动器均分离,发动机和两个电机工作;
(3)混合动力模式:制动器B2锁止、大电机2和发动机共同提供驱动力矩。
本文中主要研究纯电动与e-CVT混合动力模式之间相互切换的协调控制策略。
1.2 复合功率分流系统动态建模
由于行星齿轮的质量很小,可等效为理想的转矩传递元件。因此,在进行动态分析时,考虑发动机和两个电机的转动惯量,忽略系统的弹性与阻尼和各个齿轮的转动惯量,将行星齿轮系等效为图2所示的动力学模型。根据定轴转动定律,可以分别得到输入轴、电机1轴、电机2轴和输出轴的转矩平衡方程:

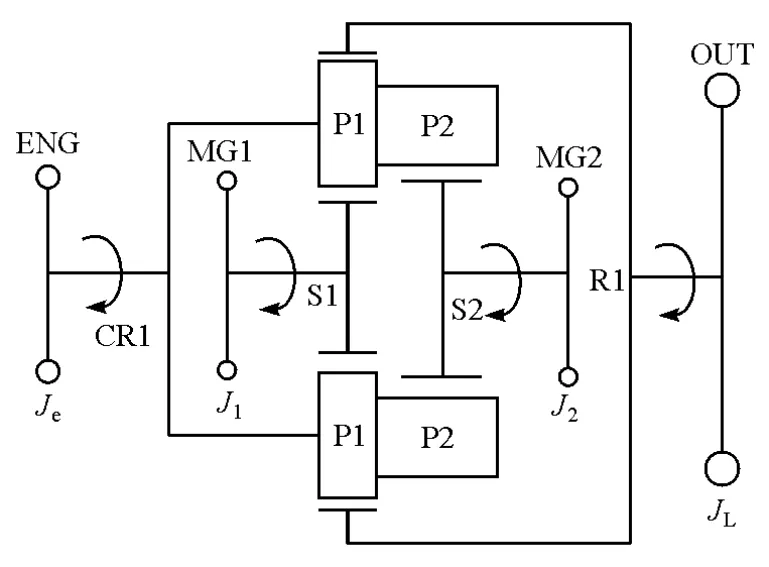
图2 传动系动力学模型
式中:T为转矩;J为转动惯量;α为角加速度;角标e代表发动机;角标1和2分别代表电机1和电机2;角标L代表输出端负载;角标S1,S2,CR1和R1分别代表小太阳轮、大太阳轮、前后排共用行星架和共用齿圈。
双行星排系统的转矩和转速平衡关系为

式中:ω为转速;ρ1和ρ2为前后行星排特征参数,即齿圈与太阳轮齿数之比。
因为不考虑系统的阻尼和弹性,所以由同一根轴连接在一起的元件角位移、速度和加速度相同。
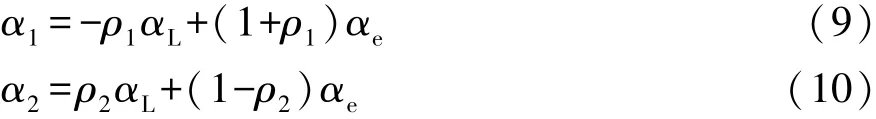
对式(7)和式(8)求导,得出双行星排系统角加速度之间的关系:结合传动系输入轴、电机1轴、电机2轴和输出轴的转矩方程和双行星排转速转矩平衡方程,由式(1)~式(6)和式(9)~式(10)可导出系统输入输出轴的动力学方程:
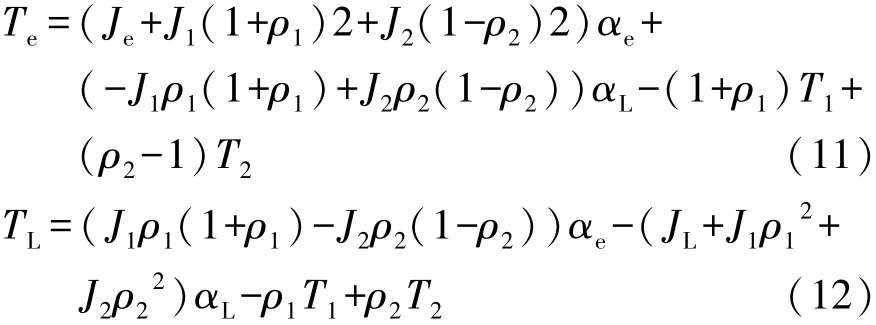
1.3 纯电动至e-CVT混合动力模式切换过程分析
下面对复合功率分流系统纯电动与e-CVT混合动力模式之间的切换过程进行分析。
从纯电动至e-CVT混合动力模式的切换过程包括B1打开、发动机起动和转矩切换3个阶段,其杠杆图如图3所示。假设车辆初始运行在纯电动模式,如图3(a)所示,制动器B1锁止发动机轴,由电机2单独驱动车辆前行。当接收到模式切换指令后,进入图3(b)所示的双电机纯电动模式,制动器B1打开,协调电机1和电机2转矩,保持发动机轴转速和转矩依然为零,不与制动器产生干涉;制动器B1完全打开之后,进入发动机起动状态,如图3(c)所示,需要协调电机转矩将发动机转速从零增加至怠速,完成发动机起动;之后进入发动机转矩切换阶段,如图3(d)所示,发动机转矩从零增加至目标值,发动机转矩目标值由能量管理策略决定,这个阶段处于e-CVT混合动力模式。发动机转矩到达期望值时,模式切换完成。

图3 纯电动至混合动力切换过程杠杆图
从混合动力至纯电动模式的切换过程与之相反,需要切换时,发动机收到断油指令,待发动机转速降低后,制动器B1锁止行星架。
下文中将以纯电动至e-CVT混合动力模式切换过程为例,进行控制策略设计。
2 纯电动至e-CVT混合动力模式切换过程转矩分配策略
2.1 双电机纯电动阶段转矩分配
双电机纯电动阶段杠杆图如图3(b)所示,已知发动机转矩转速为零,输出端转速转矩保持不变,所以发动机和输出端加速度为零,制动器状态由锁止过渡至打开,由式(11)和式(12)可得两个电机的目标转矩分别为
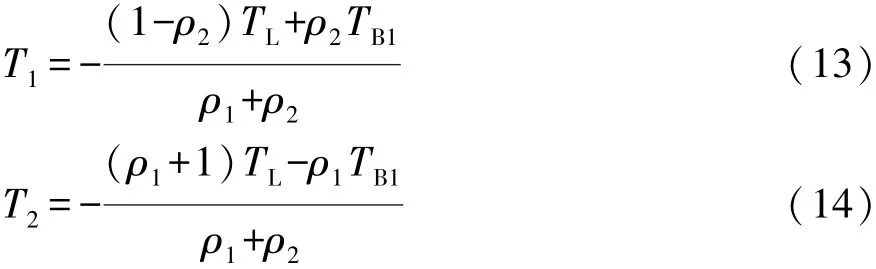
2.2 发动机起动阶段转矩分配
制动器B1完全打开之后,进入发动机起动阶段,杠杆图如图3(c)所示,这个阶段的控制目标是:车辆动力性不损失,实现发动机起动功能。与之相对应,分别制定了本阶段车辆动力性和发动机拖转控制策略。
已知发动机轴角加速度为零,发动机阻力矩可以查表,输出端转矩转速保持切换前的状态不变,由式(11)和式(12)可得两个电机动力性目标转矩为

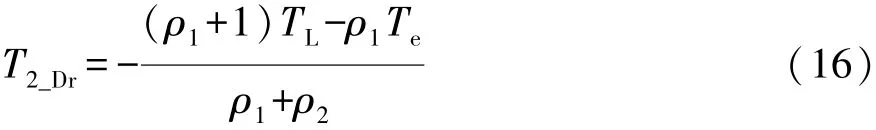
式中T1_Dr和T2_Dr分别为电机1和电机2动力性目标转矩。
发动机拖转起动过程可分为转矩开环控制和转速闭环控制两阶段。在转矩开环控制阶段,电机1利用预设拖转转矩曲线拖转发动机,使其趋近怠速。当发动机实际转速进入目标控制区域时,切换至发动机转速闭环控制阶段,利用发动机怠速和实际转速进行PID转速闭环控制,得到闭环控制转矩,之后由电机1提供发动机调速转矩。
拖转发动机时,已知预设电机1拖转转矩或闭环控制转矩,由发动机转速查表得出发动机稳态拖转阻力矩,输出端转矩和角加速度为零。只须确定电机2转矩,由式(11)和式(12)可得电机2目标拖转转矩:
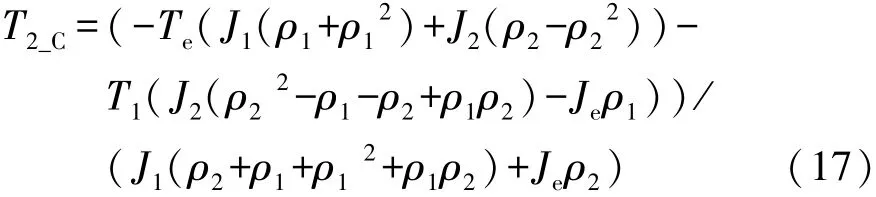
式中T2_C为用于发动机起动的电机2目标拖转转矩。
综上,在整个起动过程中,电机1和电机2的转矩如下:

2.3 发动机转矩切换阶段转矩分配
当发动机转速增加至怠速之后,发动机喷油点火,进入发动机转矩切换阶段,此阶段属于e-CVT混合动力模式,杠杆图如图3(d)所示。此时发动机转矩为零,须迅速增加到能量管理策略决策出的目标转矩值。已知输出端转矩和角加速度,然后利用当前发动机转速和目标发动机转速可得发动机目标角加速度,发动机转矩利用可测的两个电机转速转矩估算,由式(11)和式(12)可得发动机转矩和两个电机的目标转矩:
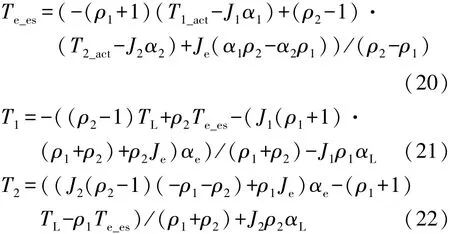
式中:Te_es为发动机估计转矩;T1_act和T2_act分别为电机1和电机2的真实转矩。
3 冲击度补偿控制策略
在转矩分配策略中,仅以模式切换过程的动力性和发动机起动性为目标,未考虑输出端转矩和转速波动。但实际系统中由于发动机阻力矩的低速脉动,制动器传递转矩、发动机和电机输出转矩瞬态响应的差异以及模型不准确等因素,都会导致模式切换过程产生系统冲击,使轮边速度波动,转矩分配策略不能完全满足平顺性要求。
针对上述问题,本文中提出一个冲击度参考模型,用以表示冲击度与两个电机转矩变化率的关系,进而得到在目标冲击度情况下,一个控制周期中电机转矩变化量的极限值。基于第2节得出的电机转矩目标值和所求极限值,制定冲击度补偿控制策略,可有效减小模式切换的冲击度。
对式(11)和式(12)求导,得到各个转矩变化率之间的关系:

考虑到输出端角加速度经过主减速器后输出至轮边,与车辆加速度成正比,而冲击度是车辆加速度的导数,所以齿圈输出端角加速度与冲击度的关系为

式中:vveh为车辆速度;r为车轮半径;i0为主减速比;j为冲击度。
根据式(23)~式(25),得出冲击度参考模型,可用式(26)和式(27)分别表示出电机1和电机2转矩变化率极限值与冲击度目标限制值jlim之间的关系为

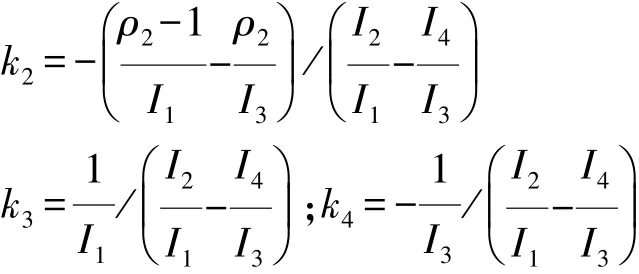
将式(26)和式(27)离散化,得出两个电机转矩变化量最大、最小极限值与目标冲击度的关系如下:

式中T为采样时间。
当两个电机在每个控制周期的目标转矩与此刻电机实际转矩的差值在式(28)~式(31)得出的两个极限值之间时,说明此时的电机目标转矩指令能满足目标冲击度的要求,可以直接输出;若超出了极限值,考虑到电机1能力有限和系统动态平衡的要求,须基于目标冲击度通过式(28)和式(31)对电机1和电机2转矩进行限制,使系统满足模式切换平顺性指标。
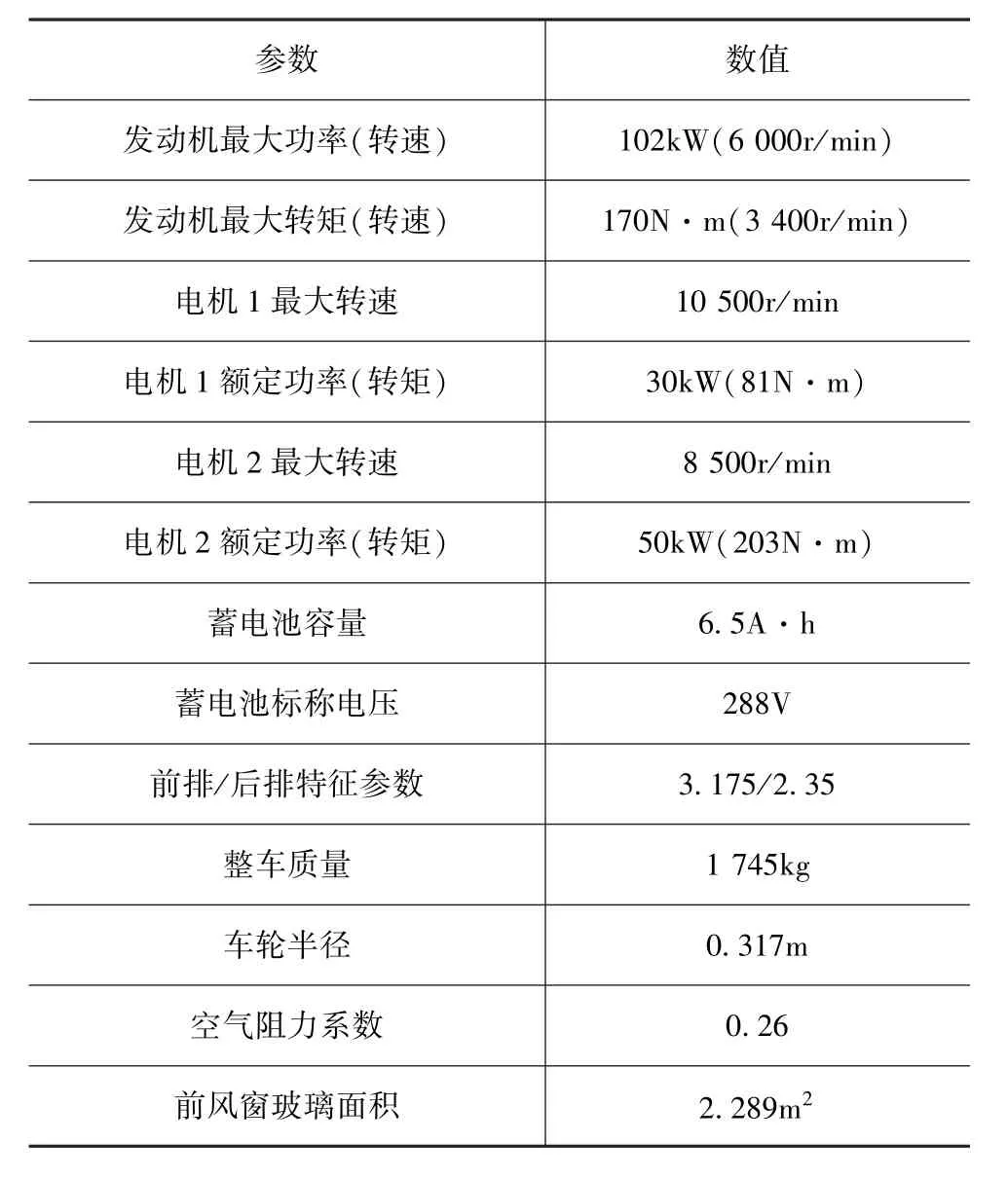
表1 整车及关键零部件参数
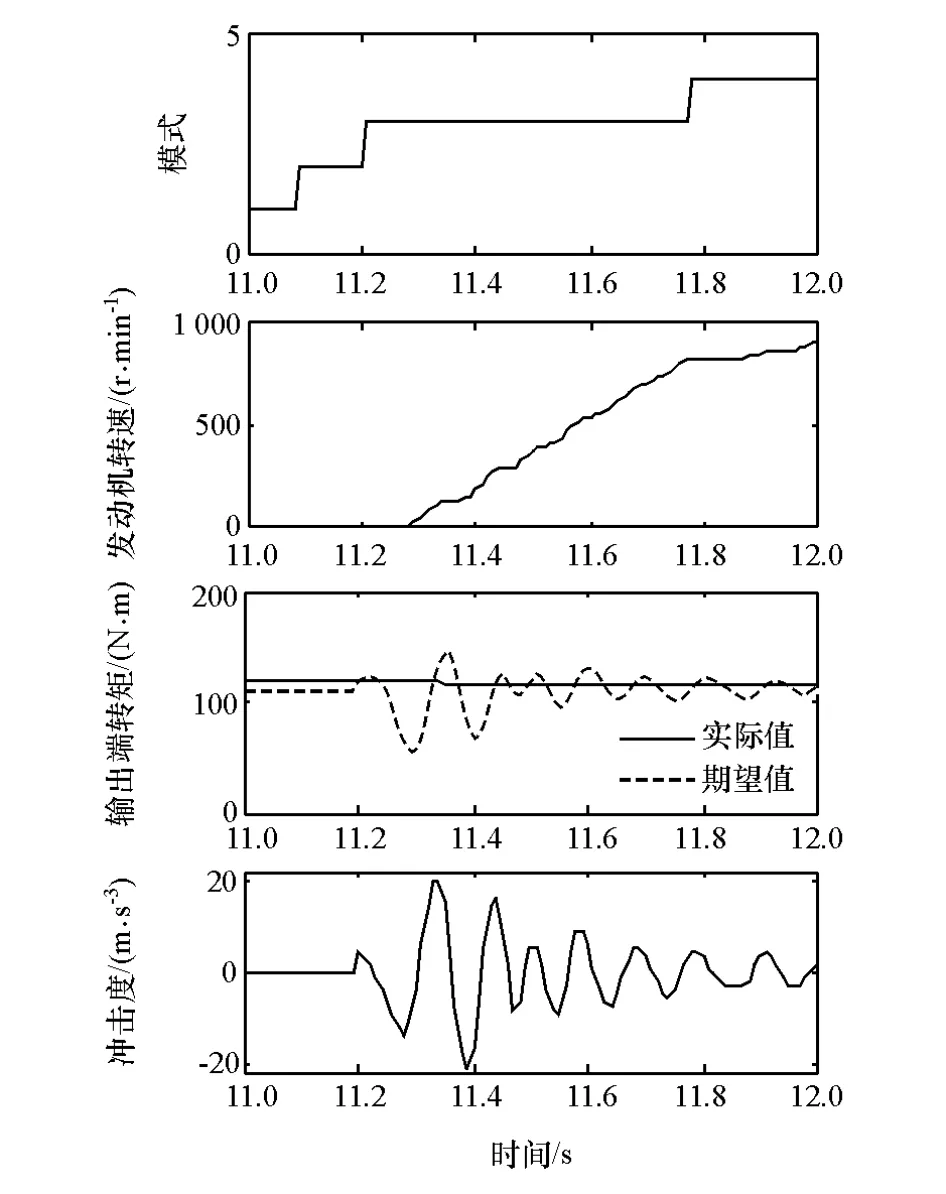
图4 纯电动至e-CVT模式切换转矩分配策略仿真
4 仿真分析
基于MATLAB/Simulink平台对模式切换过程转矩分配和协调控制策略进行仿真,以验证策略的正确性和有效性,整车及关键零部件参数如表1所示。
4.1 转矩分配策略验证
纯电动至e-CVT混合动力模式切换过程的仿真结果如图4所示,运行工况为初始速度为零,发动机加速踏板行程由零迅速阶跃至30%进行匀加速,模式图中不同数字代表运行阶段不同,1,2,3和4分别指B1锁止纯电动模式、双电机纯电动阶段、发动机起动阶段和发动机转矩切换阶段。由图4可见,系统在11.07s发出模式切换指令,首先是B1制动器打开过程,在11.19s制动器完全打开之后,系统协调两个电机转矩起动发动机,发动机的转速经过0.5s上升至怠速,经发动机点火之后进入混合动力阶段。
转矩分配策略的仿真结果表明,模式切换过程满足发动机起动性,但在切换过程输出端转矩产生波动,导致冲击度峰值达到20m/s3。
4.2 冲击度补偿控制策略验证
纯电动至e-CVT混合动力模式切换协调控制策略仿真结果如图5所示。从冲击度曲线对比图可以看出,加入控制策略后冲击度峰值为13.17m/s3,相比于加入冲击度补偿控制策略之前的20m/s3,冲击度减小约34%,基本满足国家标准。从电机转矩图中可以看出,冲击度补偿控制策略能更好地利用两个电机的转矩对输出端转矩波动进行调节,特别是电机1的转矩相比于不加控制策略时频繁的变化,减小了系统的转矩波动。

图5 纯电动至e-CVT模式切换协调控制策略仿真
混合动力至纯电动模式切换协调控制策略仿真结果如图6所示,运行工况为初速度50km/h,制动踏板行程由零迅速阶跃至30%后保持不变,进行匀减速。从冲击度曲线对比图可以看出,加入冲击度补偿策略后,冲击度峰值从之前22减小至14.13m/s3左右,即降低了约36%,基本满足国家标准。从电机转矩图中可以看出,两个电机转矩在加入控制策略前后变化的部分即为了满足系统平顺性提供的补偿转矩,可以看出电机1和电机2都对抑制系统转矩波动提供了转矩补偿。
5 功率分流混合动力变速器试验台架验证
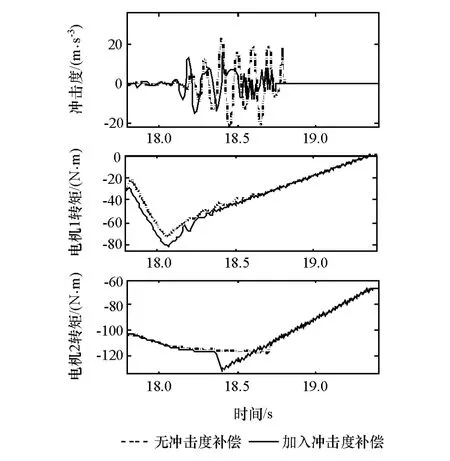
图6 e-CVT至纯电动模式切换协调控制策略仿真
为进一步验证转矩分配和冲击度补偿策略的有效性,搭建了功率分流混合动力变速器试验台架,如图7所示。台架主要由双行星排系统、制动器B1和4个电机组成,分别用电机3和电机4模拟发动机和输出端负载。

图7 功率分流混合动力变速器试验台架
图8 为功率分流混合动力变速器试验台架数据采集与控制方案,利用测量与标定软件ControlDesk,将MATLAB/Simulink中的模式切换协调控制策略下载至实时仿真控制器MicroAutobox中。控制器发送液压信号至制动器接收压力传感器反馈的油压,实现制动器控制,同时,通过Labview上位机控制电机,发送转矩指令至试验台架,并接收电机的实际转速。
利用该试验台架模拟30%加速踏板行程下,纯电动至e-CVT混合动力模式的切换,模拟制动器B1打开、发动机起动和转矩切换3个过程。分别对转矩分配策略和冲击度补偿策略进行验证,试验结果如图9和图10所示。
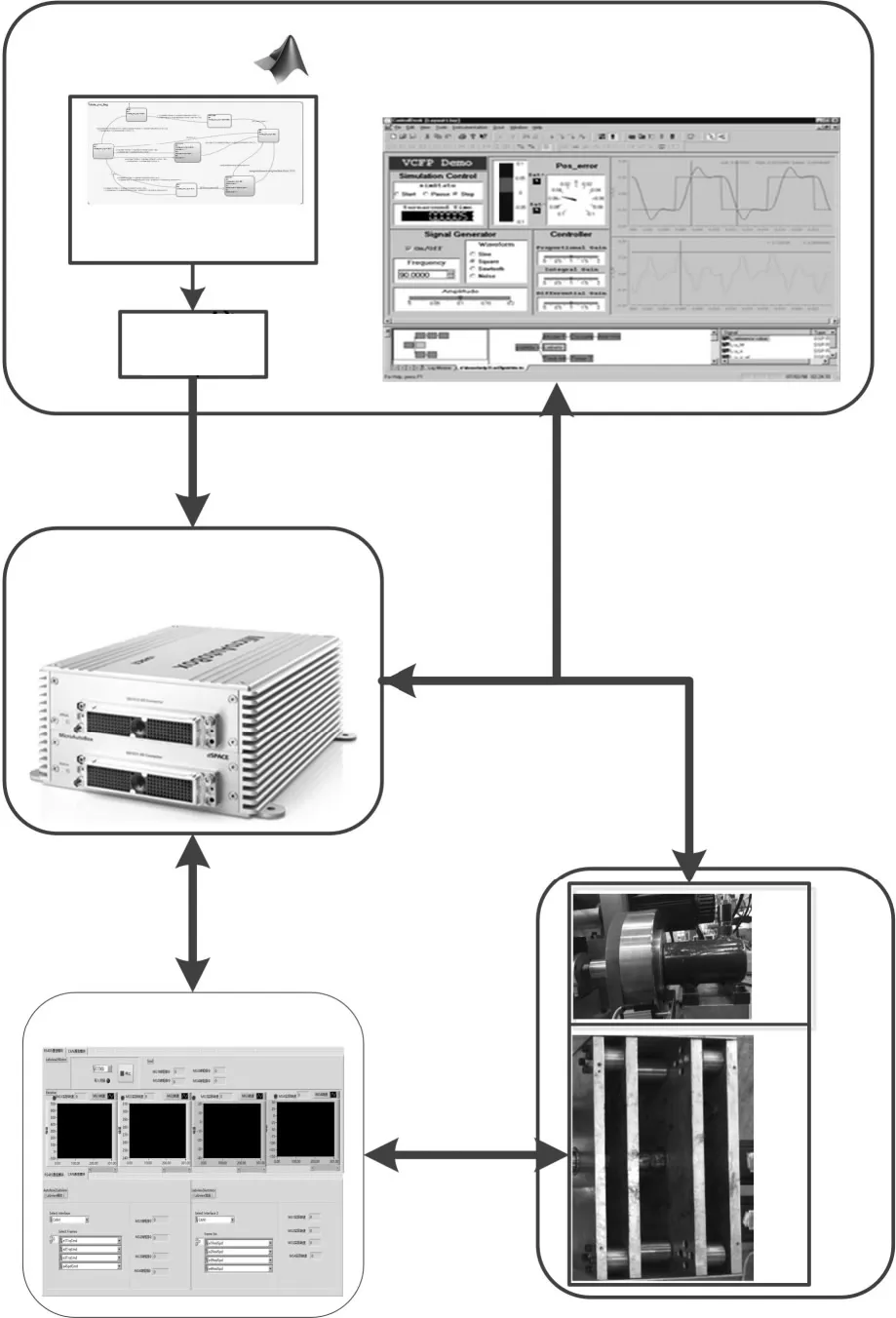
图8 试验台架数据采集及控制方案

图9 切换过程模式变化及发动机转速曲线
图9 中,模式标志1~4分别对应B1锁止纯电动模式、双电机纯电动阶段、发动机起动阶段和发动机转矩切换阶段,发动机转速拖转至800r/min用时0.5s。图10为加入冲击度补偿策略前后的试验结果对比图,冲击度峰值由30降低至15.5m/s3,基本满足国家标准。加入冲击度补偿策略之后,通过电机1和电机2转矩的快速变化,抑制了系统的转矩波动。试验结果表明,本文中所提出的转矩分配和冲击度补偿策略可实现切换过程动力性、发动机起动性和平顺性的统一,有效解决了双行星排复合功率分流混合动力系统纯电动与e-CVT混合动力模式之间切换时车辆平顺性较差的问题。
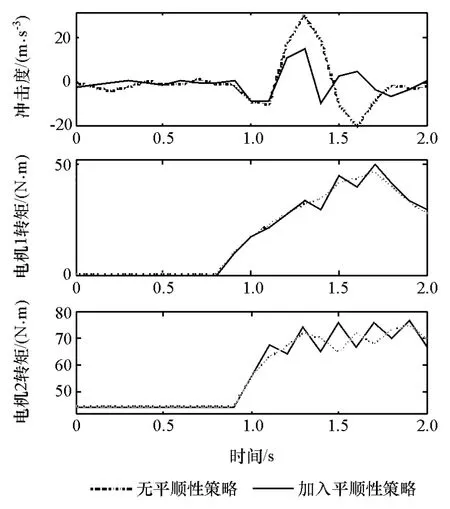
图10 纯电动至e-CVT模式切换试验结果
6 结论
(1)建立了复合功率分流系统模式切换过程动态模型,并基于杠杆图分析了纯电动至e-CVT切换的4个阶段,结合动态模型制定了每个阶段的转矩分配策略,满足了切换过程的动力性和起动性要求。
(2)基于系统的动态模型,推导出冲击度参考模型。由参考模型可得给定期望冲击度峰值时两个电机的转矩变化量的极限值,以此设计协调控制策略,满足纯电动与混合动力模式之间相互切换时的平顺性要求。
(3)基于MATLAB/Simulink平台对本文中提出的转矩分配和冲击度补偿控制策略进行离线仿真,并搭建功率分流混合动力变速器台架进行试验。仿真和试验结果表明,转矩分配策略可以满足纯电动与e-CVT混合动力模式之间切换时的动力性和发动机起动性要求,冲击度补偿策略在此基础上提高了模式切换的平顺性。
