轮毂电机驱动电动汽车的转向性能优化∗
2018-11-15张志勇黄彩霞
张志勇,张 风,黄彩霞,刘 鑫
(1.工程车辆安全性设计与可靠性技术湖南省重点实验室,长沙 410114; 2.长沙理工大学汽车与机械工程学院,长沙 410114;3.湖南大学机械与载运工程学院,长沙 410082)
前言
轮毂电机驱动电动汽车因其结构紧凑、传动效率高、转矩分配灵活等优点,成为电动汽车的一个研究热点[1-2]。但是,由于在轮毂上安装驱动电机后,会导致簧下质量增加较大,且轮毂电机的安装也给悬架的结构空间布置带来困难,设计不合理的悬架会严重影响轮毂电机驱动电动汽车的操纵稳定性[3-4]。因此,开展轮毂电机驱动电动汽车的转向性能研究具有十分重要的意义。
车轮定位参数主要包括主销内倾角、主销后倾角、前轮外倾角和前轮前束角,这些参数对车辆的操纵稳定性影响很大。如果车轮定位参数与悬架或整车性能不匹配,轻则导致整车操纵稳定性变差,重则加速轮胎磨损或出现前轮摆振。4个参数中,主销后倾角与主销内倾角主要影响转向的回正性和轻便性两方面[5-6]。由于这两个性能对车辆的操纵稳定性非常重要,因此成为研究的重点。例如文献[7]中针对车辆的转向回正性开展研究,认为小的主销后倾角和大的主销内倾角有利于改善转向回正性。但由于车辆转向的回正性和轻便性两个性能相互影响,如果仅基于其中一个性能进行参数优化,不能获得较优的综合转向性能。针对这一问题,文献[5]和文献[8]中提出了基于转向回正性和轻便性建立的四轮定位参数的优化方法,该方法既能保证汽车良好的回正性能,又能提高汽车的转向轻便性。但这些研究是以传统车辆的前悬架为研究对象,其方法和结论未必能直接应用于轮毂电机驱动电动汽车的悬架设计。为此,文献[9]中以麦弗逊式悬架为基础,开展适合轮毂电机安装的新悬架构型研究,提出以两个独立摆臂代替单个摆臂的结构,扩展了轮内空间。虽然通过优化分析得到了悬架参数,但该研究仅验证了悬架的抗侧倾性能,且未通过实车试验来验证分析结果。
通过对已有相关研究成果的分析,基于转向性能的车轮定位参数优化存在以下两个不足:(1)已有研究基本上都是针对传统集中式驱动车辆的悬架,开展车轮定位参数优化研究,针对轮毂电机悬架的相关研究较少,特别是从改善转向性能角度开展的研究;(2)很多研究仅从理论上进行性能分析和参数优化,缺少实车试验验证。因此,本文中以轮毂电机驱动电动汽车为研究对象,首先在可利用的设计空间中开展适合轮毂电机安装的悬架设计;进而建立了基于转向性能的车轮定位参数优化模型,对转向节的硬点坐标进行优化;最后通过数值仿真和实车试验验证优化结果的有效性。
1 悬架结构设计
本研究基于众泰“云100”平台开发轮毂电机驱动系统,该车前悬架为麦弗逊悬架,安装轮毂电机的悬架如图1所示。A点为减振器与车身的铰接点,P为轮胎中心,Q为减振器与转向节的铰接点,E为转向拉杆与转向节的铰接点,D为转向梯形断开点,G′为悬架下摆臂的铰接点,H1和H2分别为下摆臂与车身连接的前后铰接点,H为摆臂中心,且G′H垂直于H1H2。在安装轮毂电机后,下摆臂的铰接点无法深入轮毂内部,只能在G′H线段附近选取另一个G点作为下摆臂的铰接点。AG′为传统集中式驱动车辆的主销,AG为轮毂电机驱动时的主销。两者相比较,易知后者的内倾角小于前者。正因如此,安装轮毂电机的悬架会对车辆的操纵稳定性产生较大影响,开展悬架参数优化的目的就是减小这种影响。在悬架设计过程中,为减小对车身的改动,将保留原悬架与车身的铰接点。因此,在可利用空间中结合原结构进行悬架杆件布置,需要确定的参数主要包括E,G和Q点的坐标值。因这3点都在转向节上,故本质上是对转向节的硬点进行参数优化。
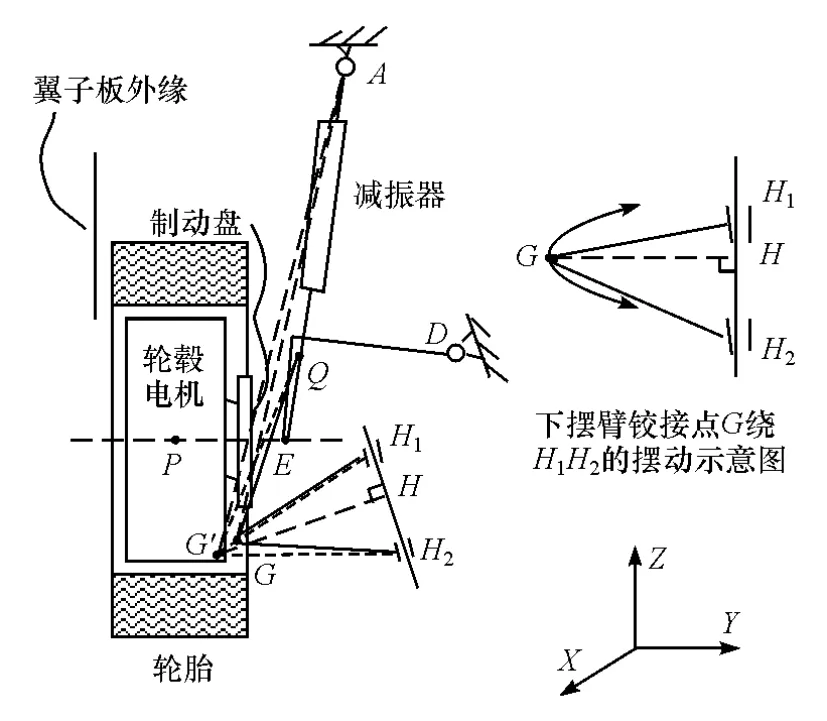
图1 安装轮毂电机的悬架结构
车轮的4个定位参数与悬架A,G,P和Q点的坐标值之间的关系如下[10]:
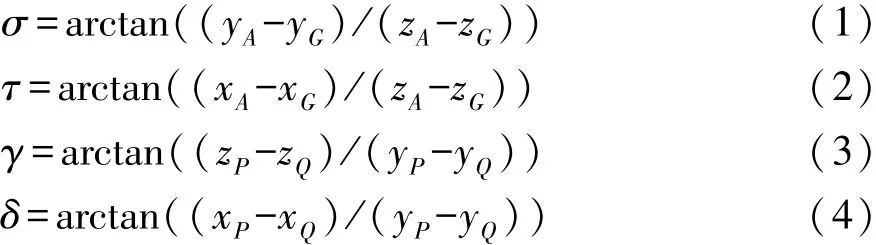
式中:σ为主销内倾角,rad;τ为主销后倾角,rad;γ为轮胎外倾角,rad;δ为轮胎前束角,rad;yA表示 A点的Y轴坐标值。其余符号依此类推。
悬架运动时,下摆臂的铰接点G以H1H2为轴线,以H为圆心摆动,其轨迹方程[11]为
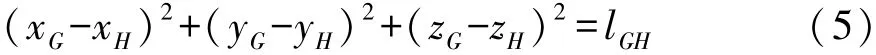
式中lGH为GH的长度,m。
在选定主销内倾角和主销后倾角的前提下,联立式(1)、式(2)和式(5)可求出 G点的3个坐标值。
前轮的前束角和外倾角是两个相互影响的角度,其关系为[10]

式中:L为轴距,m;R为轮胎滚动半径,m;l为轮胎接地印迹长度,m,计算公式为

式中:W为轮胎外径,m;Δ为垂直载荷下轮胎变形量,其表达式为

式中:N和U为系数,取值分别为11.2和0.0015b+0.42;b为轮胎宽度,m;G1为前桥垂直载荷,N;p为轮胎气压,MPa。
在选定前轮前束角和外倾角的前提下,联立式(3)、式(4)和式(6)可求出Q点的3个坐标值。
同理,E点的3个坐标值可参考文献[11],通过求解定长约束和定向约束方程组获得。
在确定E,G和Q 3个点的坐标值时,首先选取常用值作为4个车轮的定位参数,并测量安装轮毂电机后的可利用空间大小;然后以车轮中心P点为局部坐标系的原点,采用上述方法初步确定出减振器轴线与车轮轴线相交点Q的坐标为(0,180,150),转向拉杆的外铰接点 E的坐标为(-141,122,0),悬架下摆臂的铰接点G的坐标为(0,98,-163);最后再根据悬架安装空间,计算出3个点坐标值的允许变动范围,作为后续优化模型的设计变量范围。
通过车辆动力学仿真分析,比较下摆臂球铰点移动前后的转向性能,可知该点往车辆纵轴方向移动不仅会导致车辆的回正性变差,且还会增加转向力,说明在悬架中安装轮毂电机会降低车辆的转向性能。因此,研究如何改善轮毂电机驱动电动汽车的转向性能十分重要。
2 转向力矩计算
2.1 回正力矩计算
车轮转向时的回正力矩包括轮胎侧偏力引起的回正力矩、主销内倾角引起的回正力矩和纵向力产生的回正力矩,计算方法[12]如下。
2.1.1 侧偏力引起的回正力矩
由Fiala轮胎模型计算侧偏力的公式为
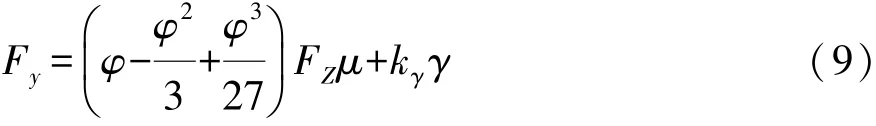
其中 φ=k tanξ/(FZμ)
式中:Fy为车轮侧偏力,N;φ为无量纲侧偏角;kγ为轮胎外倾刚度,N/rad;μ为滑动摩擦因数;FZ为轮胎垂直载荷,N;ξ为侧偏角,rad;k为侧偏刚度,N/rad。
主销后倾的总拖距为

式中:ε 为轮胎总拖距,m;ε1为气胎拖距,m;ε2为主销后倾拖距,m;r为轮胎静力半径,m。

轮胎侧偏力引起的回正力矩为一般 τ<5°,可近似认为 cosτ=1,因此式(11)简化为

2.1.2 主销内倾引起的回正力矩
由主销内倾角引起的回正力矩为
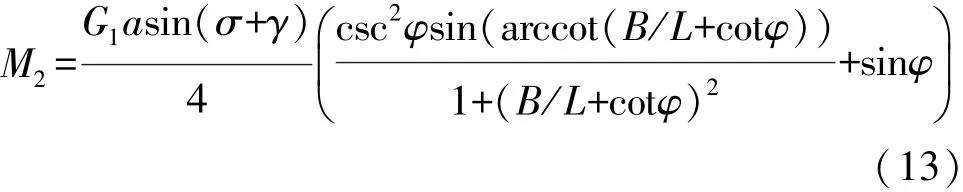
式中:φ为前轮转向角,rad;B为前轮两主销轴线与地面交点间距离,m;a为转向节节点到前轮安装中心平面距离,m。
2.1.3 纵向力引起的回正力矩
由于左右轮胎对主销产生的回正力矩,大小相等而方向相反,所以可认为相互抵消,纵向力产生的回正力矩为零。
综上所述,车轮转向时的总回正力矩为
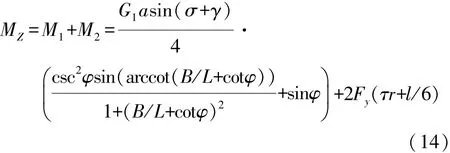
2.2 回正阻力矩计算
回正阻力矩Mf由主销回转时在衬套和推力轴承处受到的摩擦阻力矩Mf1、转向传动机构铰链中的摩擦阻力矩与转向器反转时的阻力矩之和Mf2以及路面与轮胎之间的摩擦力矩Mf33部分组成[5]。其中Mf1可由经验公式计算:

式中:f1和f2分别为上、下主销轴承与衬套之间的摩擦因数;r1和r2分别为转向节上、下销孔半径,m;lAB为转向节上下主销孔中心线间距,m;K为前桥动载系数。

3 转向性能评价指标的确定
车辆转向时,只有当驾驶员转向力矩大于回正力矩与回正阻力矩之和时,转向盘才会转动,驾驶员转动转向盘的转向力矩为

式中iT为转向系传动比。
fh越小表示转向越轻便,因此定义转向盘力矩为表征转向轻便性的评价指标。
另一方面,要实现转向轮的自动回正,转向回正力矩要大于回正阻力矩。在自动回正的过程中,回正力矩逐渐变小,当回正力矩等于回正阻力矩时,转向轮停止回正。根据式(14)和式(17)可得
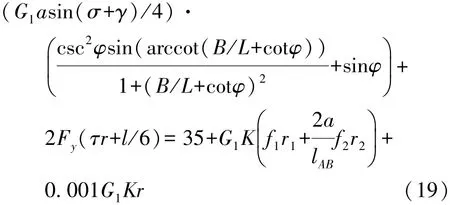
此时的转向角φ可认为是残留转角Δφ。根据残留转角Δφ与残留横摆角速度Δγ存在的关系得

式(19)可视为残留横摆角速度关于主销内倾角和主销后倾角的隐式函数。虽然残留横摆角速度一般是用于表征转向回正性的性能指标,而利用式(20),残留转角也可用于表征转向回正性能。为进一步简化转向回正性的性能指标,定义Π为

从式(21)可看出,Π是关于残留转角的一元函数,且关于自变量单调递增,因此Π也可作为表征转向回正性的性能指标。将式(21)代入式(19),可得最终的转向回正性评价指标为

从转向轻便性的评价指标(式(18))和转向回正性的评价指标(式(22))可看出,两者都是主销内倾角和主销后倾角的函数,此关系为通过优化这两个角来改善转向性能提供了可能。
4 悬架参数优化
4.1 目标函数
由于车辆的转向轻便性和转向回正性是一对相互矛盾的性能,即在改善转向轻便性的同时会导致转向回正性变差。为此,本文中以转向盘的转向力矩为目标函数,以残留横摆角速度为约束条件对主销内倾角和主销后倾角进行优化,实现在提高转向轻便性的同时得到可接受的转向回正性。在车辆转向时,转向力矩须克服转向轮转向回正力矩与转向阻力矩,车轮才能转动。如果能使回正力矩和回正阻力矩之和减小,驾驶员转动转向盘的转向力矩也会减小,转向盘就会轻便。因此,定义最小化转向盘力矩为目标函数,即

4.2 约束条件
根据国家标准[13]规定,残留横摆角速度的评分值为

式中:Δγ60为残留横摆角速度绝对值的下限值,(°)/s;Δγ100为残留横摆角速度绝对值的上限值,(°)/s。
在确定残留横摆角速度的约束条件时,首先,选择转向回正性的期望评分区间为[60,90],即认为在这个区间内的转向回正性是可接受范围;然后根据式(24)计算出残留横摆角速度Δγ的约束区间为[0.5,2];进而利用式(20)和式(21)分别计算出残留转角和Π的约束区间;最后,通过式(22)可得到关于主销内倾角与主销后倾角为函数的约束条件表达式:

由此可知,如果主销后倾角与主销内倾角满足式(25)的要求,就可保证转向回正性评分在[60,90],满足期望的转向回正性。同时,主销内倾角和主销后倾角应在合理的范围内。因此,定义主销内倾角的约束区间为[6°,12°],主销后倾角的约束区间为[1°,4°][5]。
4.3 设计变量
转向节的硬点对车轮定位参数影响较大,且不同的硬点对车轮定位参数的影响程度和方式不同。因此,在对主销内倾角和主销后倾角进行优化前,首先利用车轮同向跳动仿真,通过拉丁超立方试验方法,对转向节硬点做灵敏度分析,筛选出对主销内倾角和主销后倾角影响较大的转向节硬点作为设计变量。通过分析可知,下摆臂铰接点的3个坐标值对主销后倾角和主销内倾角影响较大,因此将其选为设计变量。
需要说明的是,在进行转向节设计时,为方便选择了车轮中心P为局部坐标系的原点,但车轮中心P在整车坐标系中的坐标为(572.25,-722.25,330),因此下摆臂铰接点的坐标值作为设计变量时需要进行坐标转换。根据前悬架的可利用设计空间,经坐标变换后确定出设计变量在整车坐标系下的寻优范围,即下摆臂铰接点的X,Y和Z轴的坐标值的取值范围分别为[562.25,582.25]、[-590.5,-610.5]和[155.39,175.39]。
4.4 参数优化
所研究的轮毂电机驱动电动汽车的主要参数如表1所示。
在Isight和Adams/Car的集成优化平台下对转向节硬点进行优化,流程如图2所示。
选择多岛遗传算法作为参数优化算法,设置种群数为8,岛数为5,遗传代数为20。Isight除能进行数据计算外,还实现遗传算法与Adams/Car之间的数据交换。首先Isight将一代设计变量的种群数据传送至Adams/Car,并实现车辆动力学模型的参数修改。利用Adams/Car提取车辆动力学模型的主销内倾角和主销后倾角后输出给Isight的Calculator模块计算回正力矩和回正阻力矩。遗传算法利用计算的力矩信号计算目标函数,进而检验约束条件是否满足,最终实现下摆臂铰接点坐标值的寻优。
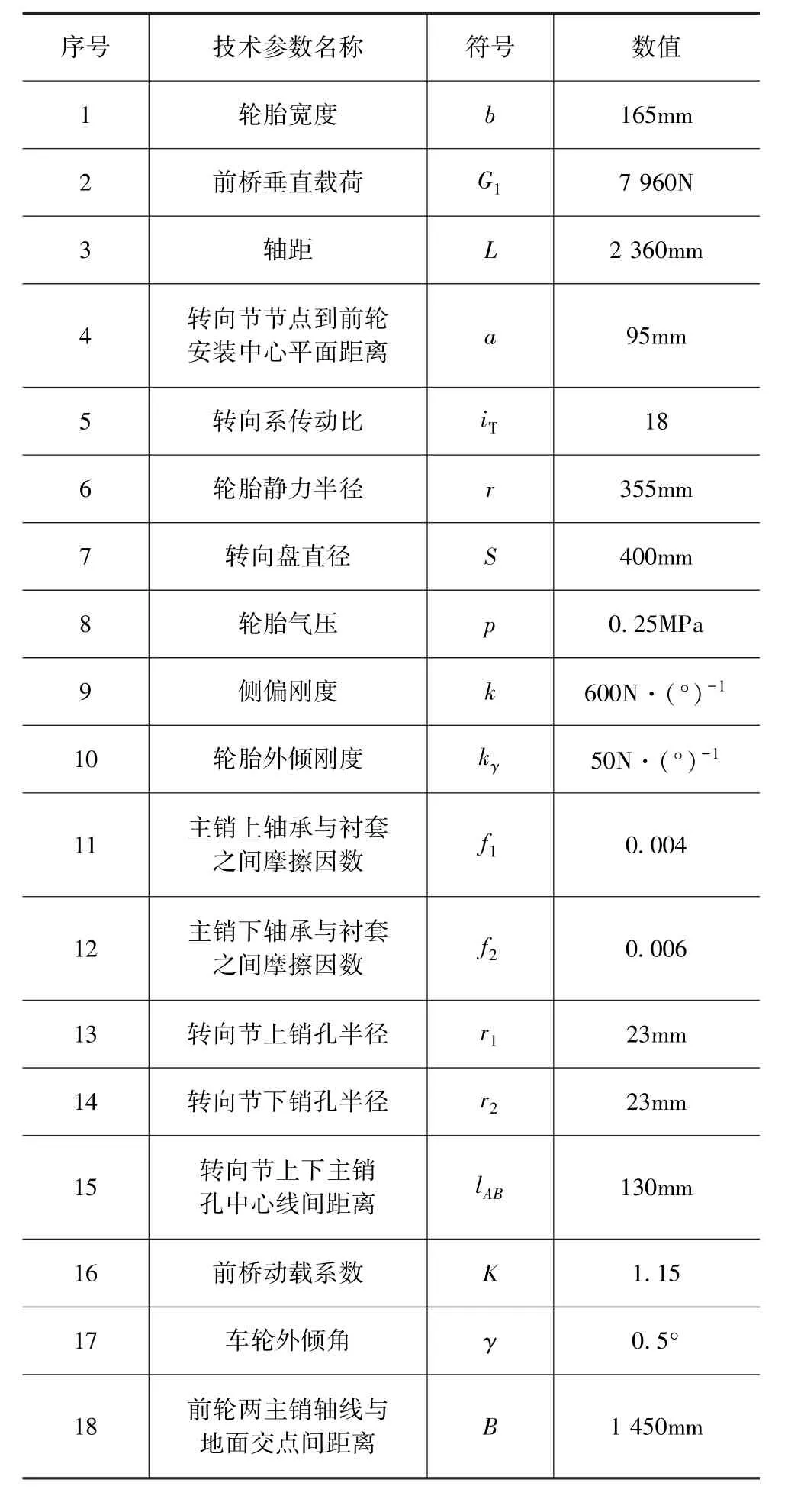
表1 车辆参数
优化前后的设计变量对比如表2所示。优化后的主销内倾角与主销后倾角分别为9.2°和2.3°,满足约束条件。

表2 优化前后设计变量坐标值

图2 参数优化流程
5 优化结果验证
通过数值仿真和实车试验两种方法进行优化结果的有效性验证。首先根据优化后的转向节硬点坐标值对车辆动力学模型的前悬架硬点进行修改,与此同时,试制了转向节样机,并装车进行实车试验,如图3所示;然后再根据国家标准的试验方法进行转向轻便性和转向回正试验;最后对比分析优化前后的转向性能。

图3 轮毂电机驱动电动汽车
实车试验中,评价转向轻便性时,将转向盘力矩转角传感器固定在实车转向盘上,转向盘的力矩和转角信号由HCZ力角测量仪采集力矩转角传感器的信号而获得。同时,HCZ力角测量仪接收GPS天线的卫星信号进行车速检测。HCZ力角测量仪通过安装在计算机上的PCM汽车动态性能测试系统软件进行数据的记录、分析和通信。评价转向回正性时,除利用HCZ力角检测仪获得车速和转向盘转角信号外,还利用课题组开发的试验程序实现STM32F4单片机对6轴传感器MPU6050信号同步采集,最终获得车辆的横摆角速度的信号。实车试验设备如图4所示。

图4 实车试验设备
5.1 转向回正性验证
依据国家标准[14]的试验方法,车辆在低速下直线行驶,然后转动转向盘,使车辆沿半径为15m的圆周行驶。调整车速,使侧向加速度达到4m/s2。稳定转向盘与车速,3s后松开转向盘并记录松开后4s的横摆角速度。试验过程中,向左和向右转向各3次,优化前后的转向回正的横摆角速度曲线如图5和图6所示。
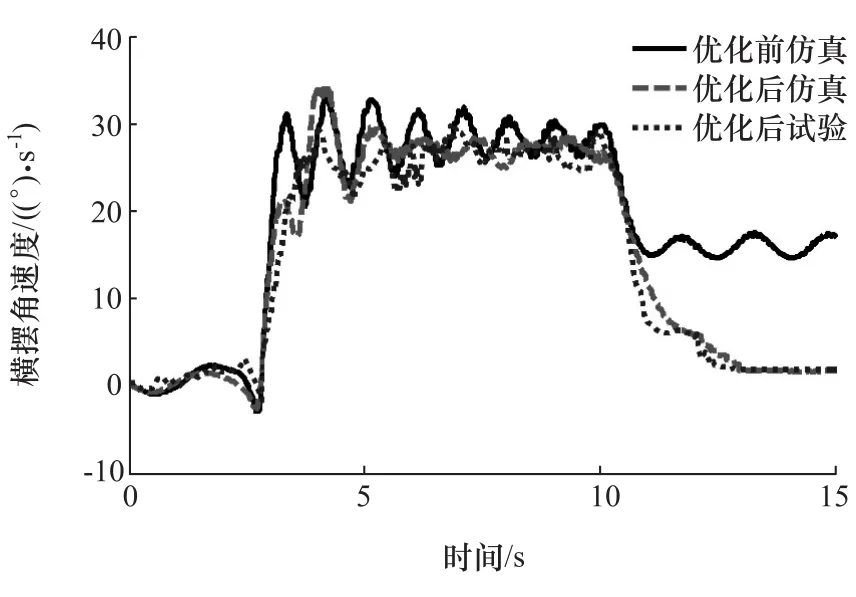
图5 左转时的横摆角速度
由图5和图6可知,车辆在左转和右转两个工况下,从10s开始到转向盘回正结束,优化后的横摆角速度比优化前的横摆角速度明显减小,说明优化后的车辆回正性得到了改善。另外,优化后仿真的横摆角速度与试验的横摆角速度比较接近,说明建立的车辆动力学模型具有较高的精度,能准确反映车辆的动力学性能。
根据国家标准[14],计算3s后的残留横摆角速度和横摆角速度总方差两项评价指标。
(1)第i周的横摆角速度总方差为
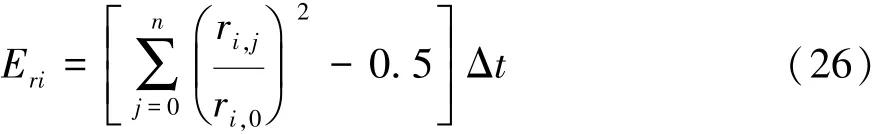
式中:ri,j为第 i周(i=1~3)横摆角速度响应时间历程曲线瞬时值,(°)/s;ri,0为第 i周(i= 1~3)横摆角速度响应初始值,(°)/s;Δt为采样时间,s。
(2)横摆角速度总方差均值为

转向回正性的两项评价指标结果如表3所示。在获得转向回正性评价值的基础上再进行评分,最终获得两项指标的统一评分。其中,残留横摆角速度的评分根据式(24)计算评分值NΔγ。横摆角速度总方差的评分值为
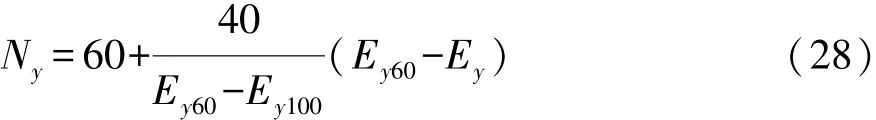
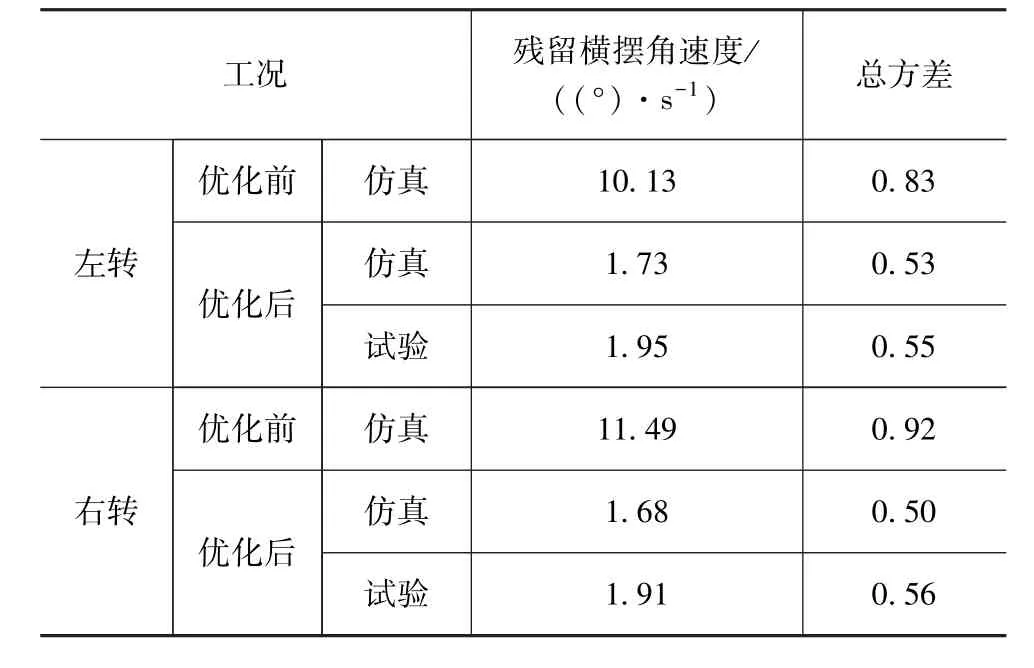
表3 优化前后转向回正性能评价值
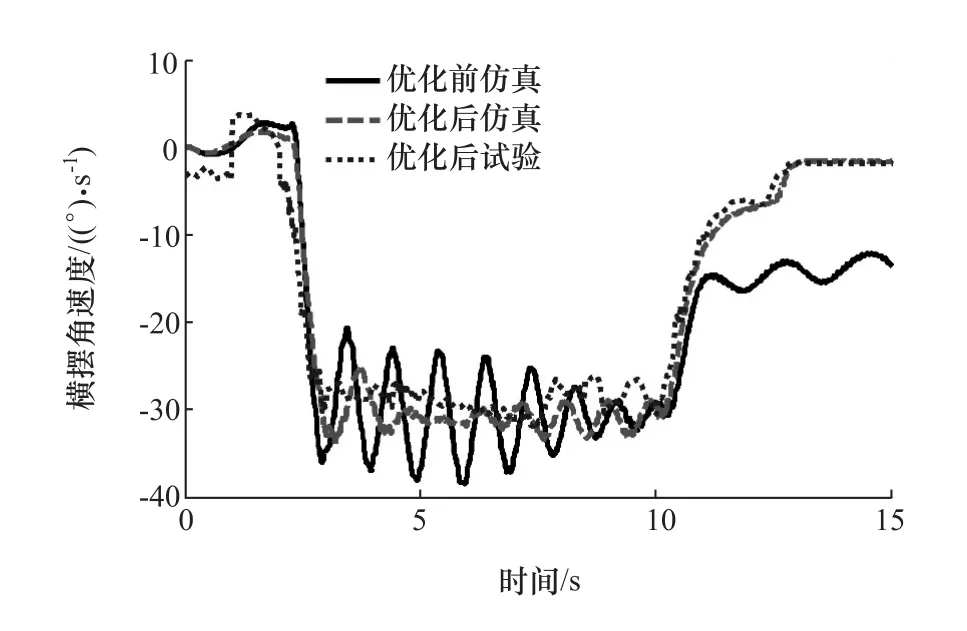
图6 右转时的横摆角速度
式中:Ey60为横摆角速度总方差的下限值;Ey100为横摆角速度总方差的上限值;Ey为横摆角速度总方差的试验值。
转向回正性的评分结果如表4所示。由表可知,优化前车辆的转向回正性能评分很低,说明转向回正性较差。优化后,在左转和右转两个工况下,数值仿真与试验的综合评分分别是 67.4,63.9和68.9,62.6。虽然通过对转向节的硬点进行参数优化后,车辆的转向回正性能得到明显改善,但评分仍较低,并未获得较优的转向回正性。
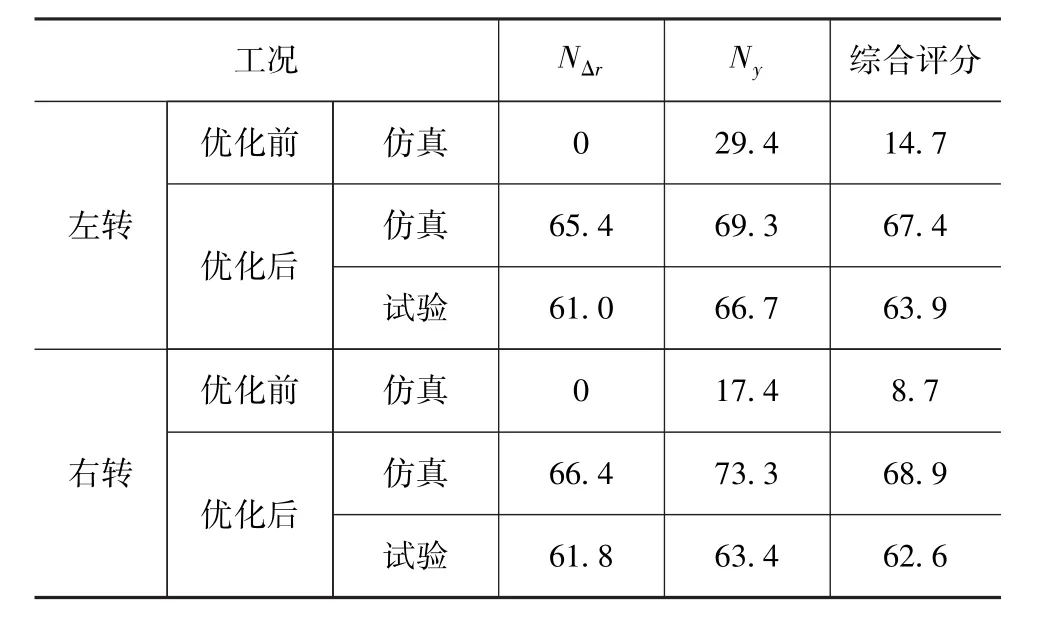
表4 优化前后转向回正性能评分表
5.2 转向轻便性验证
依据国家标准[14]对转向节参数优化前后的车辆进行转向轻便性试验。试验时,车速保持在10km/h左右,转动转向盘,使车辆沿最小曲率半径为5.5m的双纽线路径行驶,试验共进行3次。优化前后仿真与实车试验的转向力矩如图7所示。
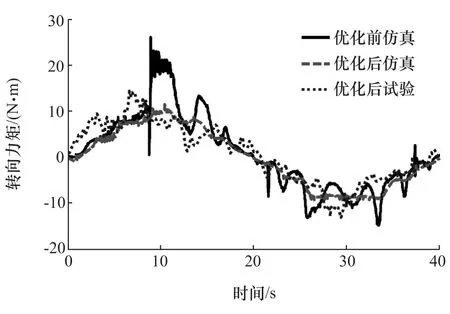
图7 优化前后的转向力矩
由图7可知,优化后仿真与实车试验的转向力矩比优化前的转向力矩明显减小,说明优化后车辆的转向盘变轻,转向轻便性得到了改善。同时,优化后数值仿真与实车试验的转向力比较接近,进一步验证了所建立的车辆动力学模型具有较高的精度。
依据国家标准[14]试验方法,表征转向轻便性的指标主要包括:沿双纽线路径转弯时转向盘最大作用力矩均值、转向盘最大作用力均值、转向盘作用功均值、转向盘的平均摩擦力矩均值和转向盘平均摩擦力均值5种,计算方法如下。
(1)转向盘最大作用力矩均值

式中|Mimax|为第 i周(i=1~3)转向盘转向力矩绝对值的最大值,N·m。
(2)转向盘最大作用力均值

式中:θi,j和 θi,j+1分别为第 i周(i=1~3)第 j和 j+1 个采样点处的转向盘转角,(°);Mi,j为第 i周(i= 1~3)第j个采样点处转向力矩,N·m。
(4)转向盘的平均摩擦力矩均值
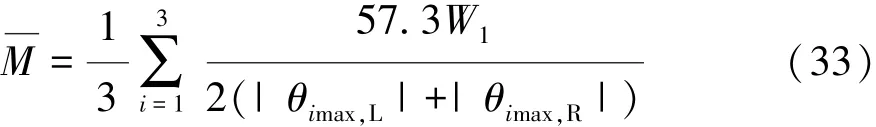
式中:θimax,L和 θimax,R为第 i周(i= 1 ~ 3)转向盘向左和向右最大转角,(°)。
(5)转向盘平均摩擦力均值

根据上述性能指标计算公式,计算结果如表5所示。
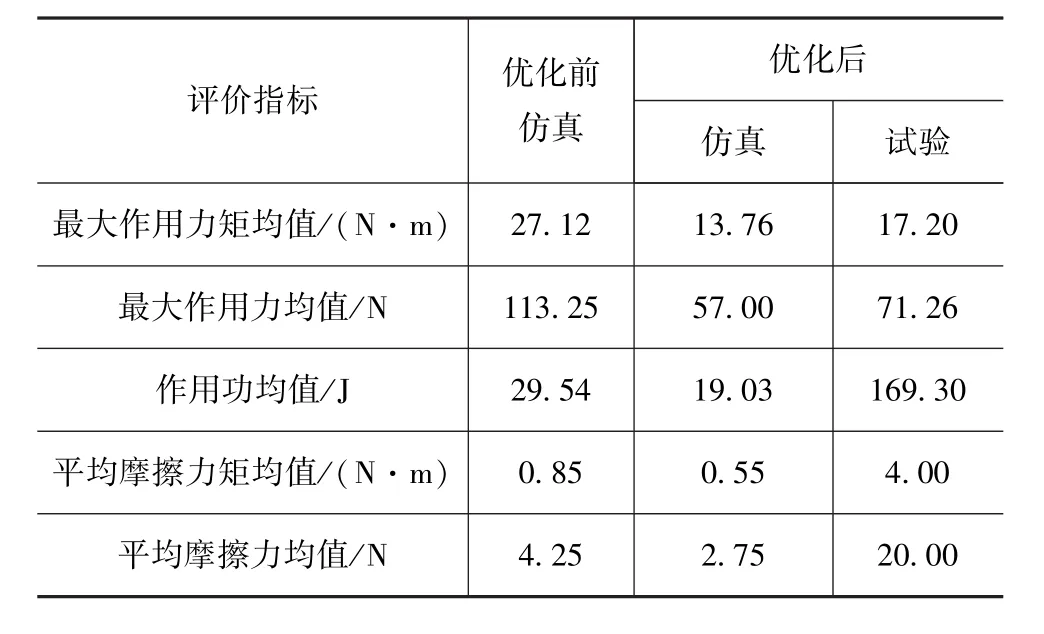
表5 优化前后转向轻便性评价指标
同理,依据国家标准[13]进行评分,内容如下。
(1)转向盘平均作用力评分
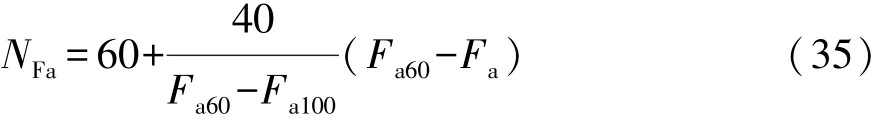
式中:Fa60为转向盘平均操舵力的下限值;Fa100为转向盘平均操舵力的上限值;Fa为转向盘平均操舵力的试验值。
(2)转向盘最大作用力的评分
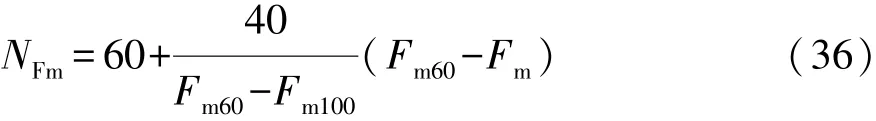
式中:Fm60为转向盘最大操舵力的下限值;Fm100为转向盘最大操舵力的上限值;Fm为转向盘最大操舵力的试验值。
(3)综合评分为

式中:ηF为与汽车最大总质量有关的加权系数,ηF=0.6+0.08Ga,Ga为汽车最大总质量,t。
根据上述评分方法,计算结果如表6所示。
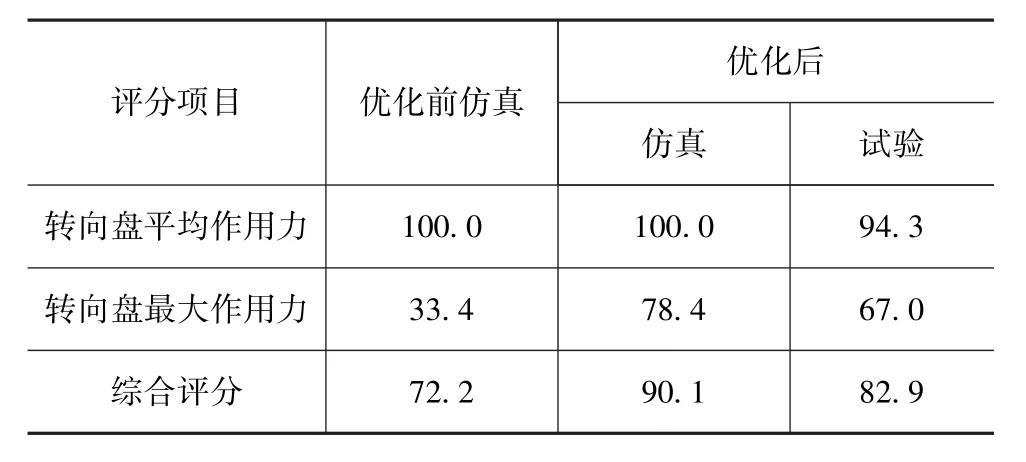
表6 优化前后转向轻便性评分表
由表6可知,优化前数值仿真的转向轻便性的综合评分为72.2,优化后数值仿真与试验的转向轻便性综合评分分别为90.1和82.9,分别提高了24.8%和14.8%,说明优化后的转向轻便性能得到了较大改善。
6 结论
基于转向性能对轮毂电机驱动电动汽车的前悬架转向节进行设计和参数优化,并通过数值仿真和实车试验进行优化结果的有效性验证,得到如下结论。
(1)以转向轻便性为优化目标,将转向回正性处理为约束条件的方法,能确保获得较优的综合转向性能。
(2)数值仿真和实车试验均表明,优化后的转向节使车辆的综合转向性能得到明显改善。
(3)在不修改悬架与车身连接硬点的条件下进行转向性能优化,由于优化空间较小,获得的转向回正性一般。因此,有必要针对轮毂驱动电动汽车开发全新的悬架系统。
