基于MATLBA的自动贴标机的参数寻优

惠州城市职业学院 刘锦杭

贴标机是一种为包装或产品添加标签的机器。它不仅具有美观的效果，更重要的是可以实现产品销售的跟踪管理，特别是在制药，食品等行业，贴标机是现代包装的组成部分。为使生产效益最大化，贴标机的贴标故障率往往需要降到最低。本文从贴标机的三个参数作为分析因子，利用神经网络软件MATLAB对系统进行训练学习，建立系统的神经网络模型。最后在此模型下，进行参数寻优，实现系统参数的优化，达到了最优故障率。

一、参数分析

贴标机在运行过程中，最重要的设定参数主要有三个，分别是步进电机速度、电磁铁打开延时、电磁铁关闭延时。对于电机速度，如果电机速度设定太高故障率会升高，如果速度太低，效率会降低。所以电机速度应该设定在一个合理的范围。对于电磁铁打开延时，因为电磁铁打开延时的计时时刻为电机启动瞬间，如果该延时设得过短，会导致回收轮在运动中，压标轮就已经执行压标动作，导致标带扯断；如果设得过大，效率会降低。对于电磁铁关闭延时，因为电磁铁关闭延时的计时时刻为打开电磁铁瞬间，如果该延时设得过短，会导致压标不成功中；如果设得过大，效率会降低。

综上所述，步进电机速度、电磁铁打开延时和电磁铁关闭延时三个参数必须设定为一个合理值才能使系统运行在最佳状态。在系统实际运行中，对三个参数分别设定不同值，测得系统贴标失败率如表1-1所示。

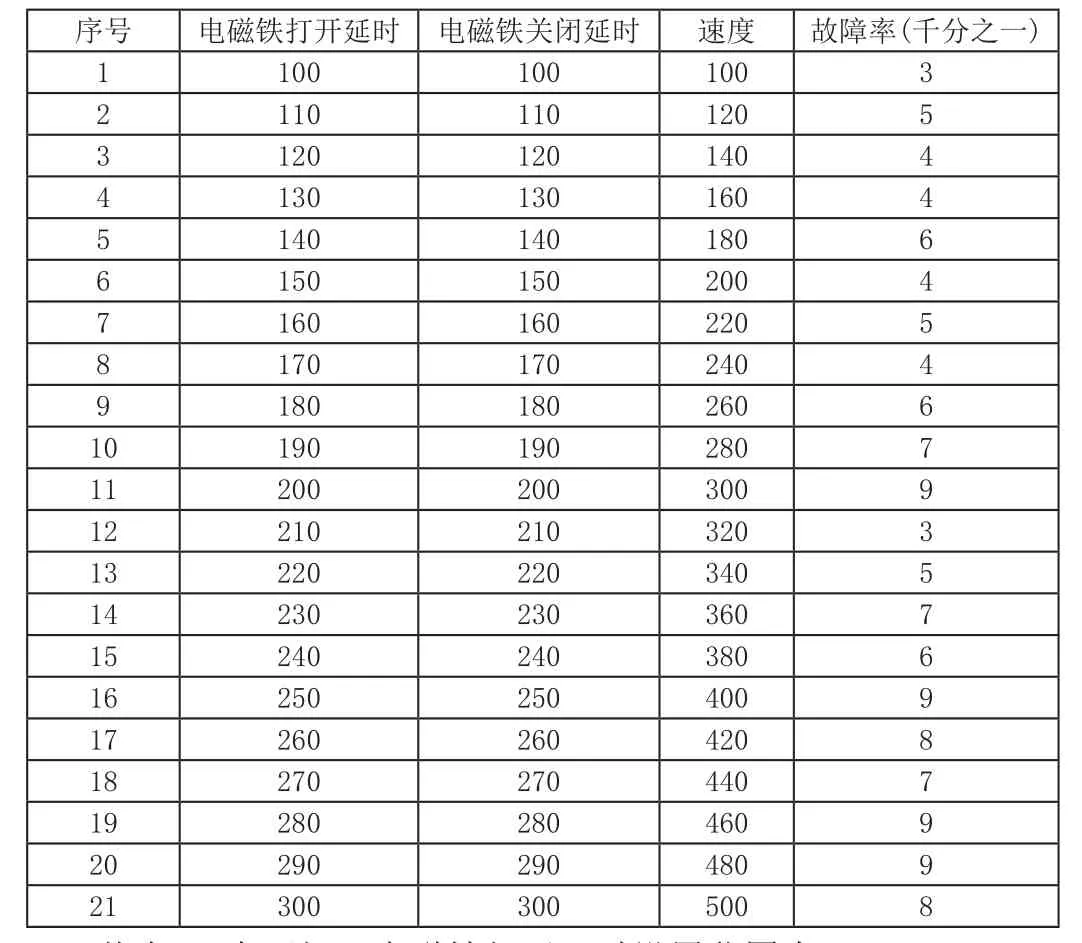
表1-1 不同参数下贴标故障率

从表1-1中可知，电磁铁打开延时设置范围为100ms～300ms之间；电磁铁关闭延时设置范围为100ms～300ms之间；步进电机转速设定范围在100～500r/min之间；标签定位检测时间为50ms～150ms之间；光纤灵敏度在400～600之间。假设设定时间分辨率为1ms，光纤灵敏度分辨率为1，则参数设置组合可与200×200×400×100×200=3200亿种组合。这是非常庞大的设置组合，不可能所有组合一一设定进行测试。由于人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时就可以得到最接近期望输出值的结果。贴标系统的贴标失败率和三个参数之间的关系是复杂的非线性关系，可通过神经网络对系统进行训练学习，建立系统的神经网络模型。最后在此模型下，进行参数寻优，实现系统参数的优化。

二、MATLAB神经网络应用

MATLAB具有强大的数学分析功能，其在神经网络分析方面，同样表现出强大的分析能力。在训练神经网络前，需要对数据进行预处理，一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法。

1.数据归一化

进行数据归一化，就是将数据映射到[0,1]或[-1,1]或更小的区间，比如(0.1,0.9)。需要对数据进行归一化的原因主要有：（1）输入数据的单位不一样；（2）数据的范围不同，功能不同；（3）由于神经网络的输出层中的激活函数的范围是有限的，因此需要将网络中训练的目标数据映射到激活函数的范围。Matlab中数据的归一化主要采用以下两个功能函数：

（1）.premnmx

将矩阵归一化，主要用于训练数据集的归一化。

（2）.postmnmx

矩阵映射是回归到变换之前的范围。该函数主要用于将神经网络的输出结果映射到归一化前的数据范围。

2.神经网络实现函数

利用Matlab构建一个神经网络，需要使用到三个功能函数：网络创建函数newff、训练神经网络函数train、应用建立得网络进行仿真的功能函数sim。

（1）.newff函数

神经网络创建函数，使用方法：net = newff ( A, B, {C} ,‘trainFun’)。

（2）.train函数

神经网络训练学习函数，使用方法：[ net, tr, Y1, E ] = train( net, X, Y )。

图3-1 神经网络MATLAB程序流程图

（3）.sim函数

神经网络仿真函数，使用方法：Y=sim(net,X)。

三、系统参数优化

1.神经网络MATLAB代码设计

根据MATLAB神经网络建模方法，设计得神经网络参数寻优MATLAB程序流程图如图3-1所示。

首先对输入的数据进行归一化处理；然后创建网络，设定训练参数，比如训练次数、训练精度等；最后应用建立好的网络对参数进行寻优。

根据程序流程图，设计得MATLAB代码如下：

2.参数优化

在MATLAB运行上面程序，得出网路训练结果图如图3-2所示。从图中可看出，训练次数在180次的时候，训练误差达到0.01。

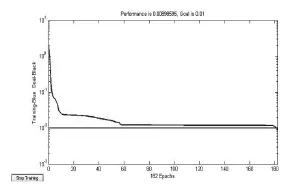
图3-2 神经网络训练结果

运行后，MATLAB打印出的最佳参数为（160,100,190），最小失败率为2.63。对贴标控制器进行设定，使得机器在参数（160,100,190）下运行，统计实际的贴标失败率。并在此参数范围内进行微调，最后确定机器在参数为（180，110，160）这个参数点运行状态最佳。

四、结束语

通过MATLAB神经网络建模以及参数寻优，确定最佳参数为（280,280,340,50,440），最小贴标失败率为0.9541。对贴标控制器进行设定，让机器在参数（280,280,340,50,440）下运行，统计实际的贴标失败率，并在此参数范围内进行微调，最后确定机器在参数为（260,290,320,60,455）这个参数点运行状态达到最佳，实测最小失败率为0.9/1000，满足2/1000的设计目标。