基于一维混沌系统的图像加密算法研究与分析

福建船政交通职业学院 朱 婧

随着计算机信息网络技术和图形图像处理技术的高速发展，网络技术和图形图像技术的高度集合，已经成为互联网传播中不可或缺的手段之一，也正是它们的不断发展使得人们之间的通信愈来愈便捷。而随之而来的弊端也日益突出，图像信息合成、图像信息篡改等情况也频频发生，如何在当今信息技术高速发展的社会，能让网络技术和图形图像技术更好的具有保密性、安全性，这个问题就成为近些年来信息安全技术领域里的热点。本文就是基于一维混沌理论对图形图像进行加密技术的研究与分析，具有一定的研究意义。

引言：混沌理论是非线性运动系统中一种很特别的方式，在自然界和社会科学界的各个领域中都似乎可以看见它的身影。它对一些初始值、密钥大小和随机的偏好却有着很强的敏感性，所以这些参数的变化也就会对图形图像的加密、解密产生不同的变化。现在的多媒体图形图像越来越多样化，不再像传统的图形图像一样单调规则化，它开始变得多元化，信息存储量大，安全性变高，这些传统的加密方式都无法满足它的需求。因此，在这样的环境下，混沌算法开始推广于多媒体信息的加密和解密过程中，它的运动特点符合现代多媒体图形图像的发展趋势，它在多媒体信息隐藏的实例也引起了很多研究者的关注，使用它对多媒体加密技术也得到了迅速的发展。

目前主流的混沌系统主要分两类：一种是低维混沌系统，另一种是高维混沌系统。低维混沌系统如一维混沌系统，它则是通过一个初值变量值和混沌参数进行加密解密，它的算法例如有Logistic、Sine、Tent映射等，这种的算法结构和混沌轨迹相对简单。本文也是通过对一维混沌系统中的Logistic算法理论为依据，对一张1024*760图片为例进行研究，分析它通过初始值和参数如何对图像进行加密解密的，分析它对于一些参数的变化又会产生出怎样的敏感变化。

1 一维混沌算法理论

在古代，无论是在中国还是西方,混沌都表示宇宙形成之前的元气(无序状态)。如三国时期曹植的《七启》中有“夫太极之初，混沌未分”。古希腊和巴比伦对混沌一词也有类似的意义，例如将混沌描述为“在秩序的宇宙之前就已存在的无秩序、无定形的物质”。以后，混沌就表示完全无序或彻底混乱的意思（刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2005）。

研究对多媒体图形图像的加密解密技术，是目前现代计算机网络安全技术的一部分。混沌技术是物理动学中一种非线性的运动形式，在自然界、社会科学界甚至是生物学界都能看见它的影子。这是因为它的运动轨迹是一种表面上无特点的，实则有很多的有规则的运动。所以根据混沌的特点，人们目前在图形图像中最常都会引入混沌理论，它也是扩散加密思想的一个分支。科学家们希望通过结合它的一些特性，对图形图像起到一个很好的保护作用。混沌理论不仅可以将加密对象映射成为非线性，也会对密钥的变化敏感，产生不同的结果。其中Logistic、Sine、Tent等算法就是一维混沌算法的典型代表。本文则以一维混沌理论中的Logistic算法为代表，通过一张1024*760通过对其初始值、参数等进行变化来分析这种算法在加密和解密图片时它的变化，来了解一维混沌理论在多媒体图片信息安全方面的深层研究。

1.1 Logistic算法

一维混沌理论中的Logistic算法可以说是在混沌理论中一个从数学角度上来说结构相对简单的算法。很多年前就有不少的科学家研究过它和应用它。事实证明，这种算法虽然结构相对简单，但是丝毫不影响它在信息安全中的作用。所以，这些年Logistic算法还是在不少的领域都得到了应用。一维混沌Logistic算法具有混沌参数u和xn取值区间，并且这三种映射的混沌参数u和xn取值区间相同。而其他的一维混沌系统尽管混沌参数u和xn取值不相同，但是都可以通过变换公式，使其相同（王光义,袁方.级联混沌及其动力学特性研究[J].物理学报,2013,62(2):020506-10）。

Logistic、Sine、Tent系统表达式如下：

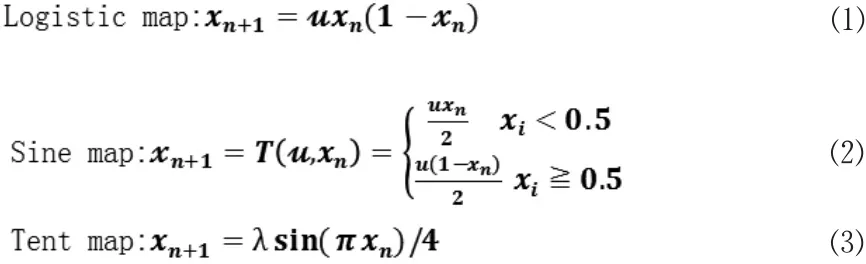
其中本文所选取的一维Logistic算法的是公式（1）。在这个公式里，u作为这个公式中的一个参数，这个参数影响了Logistic算法的混沌状态，而x也是有取值范围的，而如果超出这个范围，最后的值将越来越趋于一个值。所以，从这个公式中，我们不难看出Logistic算法具有以下几个特点：

（1）初始值敏感性。xn在（1）公式中的作用是举足轻重的。它的变化会导致整个公式的结果发生重大的变化。对初始值的敏感就是混沌理论的显著特征之一。只要初始值发生微小的变化，都会影响整个混沌的运动轨迹。

（2）随机性。而xn是随机的，只要在混沌区间内，它都可以取值。混沌系统运动表面上看表现出很强的随机性，是一种不受控制的运动，实质上混沌轨迹是由确定公式决定的，产生的混沌序列是一种伪随机的（王凤英.基于混沌理论的图像加密技术研究[M].TN393.08,U.D.C.64孙燮华.图像加密算法与实践——基于C#语言实现[M].北京:科学出版社,2013）。

（3）确定性。u和初xn决定了xn+1，也就是混沌状态。

所以，由此我们不难看出混沌算法的随机性、确定性和初始值的敏感性，都使得混沌理论在多媒体图形图像加密方面的应用中隐藏着巨大的发展方向，这也应该是我们日后密码研究的方向。

1.2 Logistic算法的参数分析

一维Logistic算法是一维离散混沌系统，具有运算速度快的特点，通过方程反复迭代可以产生较好的混沌序列。而初始值x0和混沌系统参数u对这个公式影响很大，也就是说产生的混沌序列值对初始状态和混沌系统参数极其敏感。其中参数u介于(0,4]，xn介于(0,1)。

对一维Logistic映射进行公式变换，可以变形得到：

当u =3时，不动点失稳，将要出现2周期态；

当u =3.4494897 时，2周期态失稳，将要出现4周期态；

当u =3.544090 时，4周期态失稳，将要出现8周期态；

当u =3.5699456 时，8周期态失稳，将要出现16周期态；

这种当控制参数变化到接近某个临界值而使系统的动力学性质发生性质变化的现象称为分岔，一维Logistic映射如上述这种依次出现周期加倍的现象就是倍周期分岔。我们可以借助分岔图：以自变量x0为纵坐标，以混沌系统参数u为横坐标，来研究系统的状态演化规律。一维Logistic映射的分岔图如图1-1所示。

图1-1 Logistic分岔图

当参数u达到极限值，即u =3.5699456 时，混沌系统的稳态解周期为∞。也就意味着当u ∈(3.5699456,4)时，Logistic映射进入一种随机分布的状态，即进入混沌状态。当参数u不断增加值，系统也会不断的呈周期性分岔进入混沌；而当u = 4时，成为满混沌状态。在实际应用时为了更好的体现混沌运动状态，u的取值范围一般会从(3.5699456,4)取值。

2 Logistic算法在加密图像中的应用

数字图像是目前最流行的多媒体形式之一，在政治、经济、国防、教育等方面均有广泛应用。对于某些特殊领域，如军事、商业和医疗，数字图像还有较高的保密要求。图像加密的思想就是通过一组可逆的数学变换把图像伪装成伪随机性的乱码，使未授权者不能理解它的真实意义，以实现图像保护的目的（Guo Jiansheng,Zhang Cong-e,Jin Chenhui.Attack with Know Image to a Symmetric Image Encryption Scheme.Systems Engineering and Electronics,2007,29(3):341-345）。基于混沌系统的图像加密技术是最近这些年才发展起来的，但是混沌在图像加密中所表现出来的优势使混沌图像加密算法迅速发展。混沌图像加密技术就是把原始图像作为明文对它进行加密，先将图像按照某种编码方式转化为二进制数据流，再对图像数据流利用由混沌系统生成的混沌序列进行加密。国内外学者结合已有的其它保密技术已经提出了许多基于混沌系统的图像加密算法（Tiegang Gao, Zengqiang Chen.A new image encryption algorithm based onhyper-chaos.Physics Letters A,2008,372(4):394-400;Shubo Liu,Jing Sun,Zhengquan Xu.An Improved Image Encryption Algorithm based on Chaotic System.JOURNAL OF COMPUTERS,2009,4(11):1091-1099;K W Wong,B S H Kwok,W S Law.A fast image encryption scheme based on chatic standard map.Phys.Lett.A,2008,372:2645-2652;Tiegang Gao,Zengqiang Chen.Image encryption based on a new total shuf fl ing algorithm.Chaos,Solitions & Fractals.2008,38(1):213-220）。为了展示研究分析，我们设计选取以Logistic算法为例，介绍混沌算法在引进图形图像中是如何完成加密和解密的，在这个过程中又有哪些特点。

2.1 一维Logistic混沌图像加密算法

自混沌算法应用到多媒体加密技术中来之后，很多的混沌算法得到了人们的关注，这些混沌算法众多，可以按照各种方式对其进行划分，例如加密图像的类型、加密方法的维数等。而本文所阐述的一维Logistic算法就是混沌映射算法中的一种。

为研究分析一维Logistic映射伪随机序列的加密特性，我们采用对像素点值进行加密的思路，先生成一维Logistic映射序列，取整，在对像素点进行异或即可，这种算法简单，加解密速度更快。

上式R即为最终加密完的序列，最终在把R序列转换为二维图形矩阵，输出完整的加密图像。由于只做了异或，因此解密时，在此生成同样的序列，再次异或，即可得到解密图像。

2.2 仿真实验

现在我们就以一张1024×760大小的灰度图像为例，取密钥为代入上式，获得混沌序列，对图像进行加密处理。仿真实验结果如图2-1、图2-2所示。

从图2-2加密后原图的图片来看，密文图像完全变为了均匀分布的杂点图，无法看出与原图的相关性。从直方图进行分析，图2-3原图的直方图左侧没有高度，代表照片几乎没有阴影，中间调也没有，而最右侧的则达到了最高处，说明原图含有大量的高光，是高调图片或过曝图片，特征值显著，易于分析。而图2-4加密后图的直方图，分布均匀，阴影高光中调近乎保持水平，仅两侧出现细微的极端值。特征值不明显。由此可以看出加密后的图像像素值分布均匀，明文的特征值被打破磨平，我们不难看出，使用一维Logistic混沌图像加密算法加密后，图片的密文和明文之间的相关性大大降低。

图2-1 原图

图2-2 加密后原图

明文与密文的直方图分布如图2-3、图2-4所示：

图2-3 原图的直方图

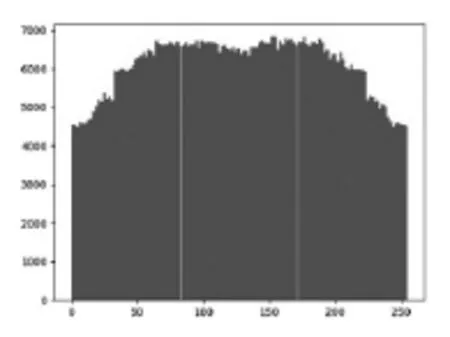
图2-4 加密后图的直方图

3 一维Logistic混沌图像加密算法分析

一个好的加密算法应该具备防范攻击的能力，在本小章节中，我会从不同的角度分析上述的算法对图像的加密能解决哪些安全性的问题。

3.1 密钥空间分析

密钥空间大小对加密算法是很重要的一个指标，它直接决定了该算法对于抗穷举类型攻击的能力。对于本文上述所提出的图像加密算法，它的密钥空间分析可以有这样的结论，密钥是Logistic映射的初值，u是Logistic映射参数，是初次自迭代次数，均采用double类型，精确到小数点后15位，采用int类型，取正整数，最大值2147483647。则密钥空间为从这点中我们不难可以看出来，这个算法的密钥空间足够大，具有一定的抗穷举攻击，可以保证部分安全性。

3.2 相关性分析

一张图片的像素点与它临近像素点是有很高的相关性，其表现也就是数据冗余特性，而本文所使用的算法就是为了破坏该图片中相邻像素点的相关性，从而达到密文无法识别该图片的目的。在上述的例子就分别从原图和加密后的图像中，抽取垂直、水平、对角线上随机抽取1000个像素点进行相关性测试，测试公式如下：

对公式进行变换，得到如下公式：

在上述公式中，x和y分别代表的是加密图片中两个相邻像素的灰度值，而rxy为相邻像素的相关系数。对加密后的图像进行分析计算，结果如表1所示。

表1 加密前后图片的相关分析表

从表1中可以看出，该图片的加密图在各个方向的相邻像素间的相关性系数都比选取的0.01系数小，为了更好的看出相关性分布，我们可以从下面的图3-1所绘制的相关性图进行对比。我们不难看出原始图像素之间的相关性还是很高的，而加密后图像像素点分布扩散，其相关性也得到了很好的降低，达到了我们加密原图的目的。

图3-1 加密前、后图片相关性分析图

3.3 信息熵分析

图片的熵值能反映出灰度图像中灰度值的分布情况。熵值越大，说明图片中灰度值分布越相同。而信息熵它也可以是一个随机数，随机变量的不确定性。信息熵的通用公式如下：

参数说明：F：灰度值；P(L=l)：像素值为l的百分比；IFE：信息熵。IFE的值越大，就表示该图像的随机性越高，越混。对于一般的灰度图像而言，灰度图的灰度值是介于0～256之间，那么对应的IFE理论最大值为8。信息熵计算如表3-1所示：

表3-1 图片加密前后熵值变化表

由表3-1可以看出，尽管本文设计的加密算法，仅仅只利用一维Logistic序列进行异或处理，产生的加密图LFE值就已经很趋近与8了。由此可以得出结论，在本文中设计的基于一维混沌系统的图像加密算法，可以获得很好的加密效果。

3.4 密钥敏感性分析

混沌算法是对初始值高度敏感的，初始值发生微小的变化，经过算法所产生的混沌序列也将差距甚大。一维Logistic映射算法亦不例外。根据本文的算法，选取初始值为0.01，分别对初值进行微小的调整，看迭代500次后的结果差距，如表3-2所示。

表3-2 初始值变化表

图3-1 使用正确相同的初值解密

图3-2 使用仅相差0.000000001的初值解密

从表3-2中我们不难看出来，即使初始值我们取的再相近，所产生的混沌序列也差距是否巨大，为了更方便直观的展示，对图像进行加密解密测试，初值使用0.01进行加密解密，在用0.010000001对加密图像进行解密，最终测试结果如图3-1和图3-2所示。

4 总结

在本文中我们详细举例说明了基于Logistic映射算法对1024*760大小的灰度图像如何进行加密和解密的。我们可以看到，通过这种算法我们可以先生成一个混沌序列对图片像素的位置进行置乱，同时也是利用这种算法再生成另一个混沌序列，然后将生成出来的两种序列运算和扩散，来过到有效加密的目的。通过上文的实例，我们可以看出，通过Logistic算法加密和解密的图片是有较好的效果的。但是，我们也看出，这里面仍然还存在着一些弊端。Logistic算法因为是属于一维也就是低维数的混沌算法，所以它在加密、解密图片方面，虽然密钥管理方便，加解密速度快，但还是相对简单简单，在图片的安全问题上还是存在一些不足的。还有，这种算法由于它的维度局限了它的密钥空间，对大的穷举类的攻击，防御上可能也会有所欠缺。因此，我们在对灰度图片进行加解密时，应该首先分析各种算法的优缺点，对于一些安全级别要求高的图片，可以采用一些高维数混沌系统和对图像像素的置乱算法，来达到对图像更为有效的加解密，提高图片的安全性。