基于封装基板上的平面螺旋电感建模与分析

2018-11-14通富微电子股份有限公司王洪辉

电子世界 2018年20期

通富微电子股份有限公司王洪辉

南通大学专用集成电路设计重点实验室孙文俊孙海燕

本文利用了ANSYS HFSS软件完成平面螺旋电感结构的优化建模。同时制造出实际的PCB平面螺旋电感。通过提取到的S参数推导出电感值L和品质因数Q，并将其与仿真结果进行对比，来验证仿真结果的正确性。此外，详细分析了金属宽度(w)、线间距(s)、匝数(n)、线圈内径(din)等几何参数对螺旋电感性能的变化的影响。将这种新颖的平面螺旋电感技术应用于低噪声放大器(LNA)的芯片封装协同设计中，并对其进行优化，最终符合LNA设计指标。

1 简介

随着通信和计算机技术的迅速发展，现代电子对射频和微波产品的需求也在不断增加。随即大量的无源器件应用于先进的射频模块中。平面螺旋电感是射频电路中最重要的无源元件之一，应用于低噪声放大器(LNA)、振荡器(VCO)、天线和滤波器（Li L,Ma K,Mou S.Modeling of New Spiral Inductor Based on Substrate Integrated Suspended Line Technology[J].IEEE Transactions on Microwave Theory & Techniques,2017,65:2672-2680;Liu S,Zhu L,Allibert F,et al.Physical Models of Planar Spiral Inductor Integrated on the High-Resistivity and Trap-Rich Silicon-on-Insulator Substrates[J].IEEE Transactions on Electron Devices,2017,64:2775-2781;Yue C P,Wong S S.Physical modeling of spiral inductors on silicon[J].IEEE Transactions on Electron Devices,2002,47:560-568）。为了满足更高的集成密度、轻重量、多功能性和低成本的射频产品的要求，基于封装基板上低损耗、高品质因数的螺旋电感是极其需要的。然而，在结构设计上，有机、陶瓷、硅等集成基板的研究大多都集中在电感器模型（Sun R B,Chang P Y,Wang T K,et al.Chip-package-PCB co-design for optimization of wireless receiver performance[C].IEEE,Electrical Design of Advanced Packaging & Systems Symposium,2012:116-119;Lopez-Villegas J M,Vidal N,Alamo J A D.Optimized Toroidal Inductors Versus Planar Spiral Inductors in Multilayered Technologies[J].IEEE Transactions on Microwave Theory & Techniques,2017,99:1-9;Fang X,Wu R,Sin J K O.Analytical Modeling of AC Resistance in Thick Coil Integrated Spiral Inductors[J].IEEE Transactions on Electron Devices,2016,63:760-766），射频集成电路中螺旋电感的设计还有待提高。螺旋电感器的优化是一个永无止境的工程，在封装基板上设计各种几何结构仍然是一个巨大的动力。

本文提出并分析了平面螺旋电感器的高性能配置。在第二节中，主要对该结构进行建模，比较计算值与仿真值之间的差异。同时，还增加了实验测量结果，验证仿真结果的正确性。第三节对相同衬底和不同金属宽度、匝数、线间距、内径等几何参数的平面螺旋电感进行了模拟分析。随着各个参数的变化，给出了一些设计规则。在此基础上，提出了一种适用于新型低噪声放大器的平面螺旋电感模型。第四部分对设计的模型进行总结。

2 平面电感的设计与分析

2.1 建模

电感分为方形电感、圆形电感、六边形电感和八角形电感。平面方形电感因其结构简单而被广泛应用。图1(a)为方形电感的结构的俯视图。几何参数被标注，w表示宽度，din表示内径，s表示间距。图1(b)给出了电感在ANSYS HFSS里面的三维结构。

图1 平面螺旋电感

2.2 螺旋电感的分析

2.2.1 数学模型

品质因数和电感值是评价无源器件性能的重要指标。在封装基板上稳定的电感值、高Q值和自谐振频率是必要的。在这项工作中，电感值和品质因数与金属宽度(w)、痕迹间距(s)、匝数(N)和内径(din)有关。这些平面螺旋电感的参数如表1所示。对于平面螺旋方形电感有效的公式可定义为（Xiao Q,Luo T,Shi Y,et al.Simple and Accurate Radio Frequency Inductance Expression for On-chip Planar Spiral Inductors[C]//International Symposium on Antennas,Propagation and Em Theory.IEEE,2008:1025-1028;Ciccazzo A,Greco G,Rinaudo S.Coupled EM & Circuit Simulation Flow for Integrated Spiral Inductor[C]//IEEE International Symposium on Industrial Electronics.IEEE,2006:1203-1208）：

Davg代表的是内径与外径的平均值，其公式为：

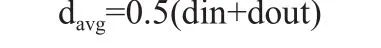
和填充率ρ的公式为：

ρ=(dout-din)/(dout+din)

方形电感器的固定系数为K1和K2分别为2.34和2.75（Itoi K,Sato M,Abe H,et al.On-chip high-Q spiral Cu inductors embedded in wafer-level chipscale package for silicon RF application[C]//Microwave Symposium Digest,2004 IEEE MTT-S International.IEEE,2004:197-200 Vol.1;Koutsoyannopoulos Y K,Papananos Y.Systematic analysis and modeling of integrated inductors and transformers in RF IC design[J].IEEE Transactions on Circuits & Systems II Analog & Digital Signal Processing,2000,47(8):699-713）。根据公式(1)和表1所示，螺旋电感的计算值为2.71nH。

表1 方形电感的参数

2.2.2 仿真和测试结果

为了与计算值进行比较，在电磁工具中建立了电感三维结构。利用ANSYS HFSS可以得到散射参数S和导纳矩阵Y。通过矩阵Y，可以根据公式(2)和(3)分别得到电感(L)和品质因数(Q)（Saberhosseini S S,Ganji B A,Razeghi A,et al.Modeling & simulation of MEMS spiral inductor[C]//Electrical Engineering.IEEE,2016）。

根据图1和表1所示，制造的电感线圈如图2所示。S参数的测量结果由9kHz到8GHz的频率范围的网络分析仪E5071C得到。

图2 制造的电感示意图

图3所示给出了仿真结果。为了验证模拟的精确性，还增加了测试结果。图3(a)和图3(b)给出了s参数和y参数的测量结果与仿真结果的比较。可以看出，测量结果和仿真结果趋势是相同的，在整个9kHz-8GHz带宽上表现出良好的一致性。通过公式(2)和(3)的转换，图3(c)和图3(d)描述了仿真结果与L和Q测试数据的对比。即使误差较小，也可以看出环路电感的设计可以很容易地针对高频率品质因数进行优化，同时将面积限制在一定的最大值。

图3 仿真和测试结果的比较

3 几何参数的比较

在实际电感设计中，电感L和品质因数Q是评价性能的标准。同时，几何参数是影响L和Q的重要因素，本节设计并仿真了几种不同几何形状的电感，并对其性能进行比较。

3.1 线圈匝数的比较

图4显示了三种平面螺旋电感，它们被选择来设计和分析n的变化。这三种电感除了匝数外，都具有相同的几何参数。金属线宽为360um，内径1440um，线间距为300um。图5为不同N时电感L与质量因子Q的比较。

图4 不同匝数的平面电感

图5 不同匝数的仿真结果比较

可以看出，基于封装基板的不同匝数，L和Q都具有相同的趋势。该值随着轮数的增加而增强。然而，自谐振频率(SRF)和Qmax有相反的趋势。随着匝数N的减小，金属损耗减小，以提高Qmax。SRF的减小主要是因为电容耦合和电感值的提高。

3.2 金属线宽的比较

图6所示为三种螺旋型电感，它们都具有不同的金属线宽w,其他参数分别设计din为1440um,s为300um,n为3。金属宽度从420增加到540um，增量为60um。仿真结果如图7所示。

图6 不同线宽的平面电感

图7 不同线宽的仿真结果比较

随着金属线宽的增大，电感的增量幅度较小。随着金属宽度从420增加到540um,Qmax增强，因为有效线宽会导致串联电阻的减少。SRF降低的原因是金属线宽的电容耦合。

图8 不同间距的平面电感

图9 不同线间距的仿真结果比较

3.3 金属线间距的比较

图8所示描述了三种类型的电感器，它们被选择用于研究和分析“s”的变化。这三种类型都具有相同的几何参数，除了在金属之间的间距。金属宽度为480um，匝数为3，内径为1440um。金属之间的间距从300增加到360um，步长是30um。仿真结果如图9所示。

图9(a)显示，当金属间距增大时，低频电感无明显变化。由图9(b)可知，由于耦合较弱，Qmax随间距的增大而减小。

3.4 线圈内径的比较

图10所示描绘了三种电感，它们被用来研究和分析不同的内径。金属宽度为360um，金属间距为300um，匝数为3。内径从1500um增加到1620um，增量为60um。图11为电感L与质量因子Q的比较。

图10 不同线圈内径的平面电感

图11 不同内径的仿真结果比较

图11(a)显示电感值随内径的增大而增大。内径的减小导致图11(b)中的Qmax，因为金属线之间的趋夫效应变得足够显著，足以诱发电流。SRF没有明显的变化。

4 5.8GHz低噪声放大器的应用

平面螺旋电感器作为一种重要的无源器件，可以应用于许多研究工作。图12为5.8GHz低噪声放大器(LNA)的电路原理图。输入匹配网络M2采用的电感L1、L2和栅源电容Cgs，电感L4和电容C4作为输出匹配网络。基于封装衬底上的平面螺旋电感理论，设计了L1、L2和L4电感。LNA提供1.8V的偏置直流电压，每个端口阻抗值为50ohm。

图12 低噪声放大器的电路图

采用触点阵列封装(LGA)来实现芯片封装的协同设计。图13为基于螺旋电感设计的低噪声放大器三维结构。对L1、L2、L3和L4进行了优化，实现了良好的性能。

图13 基于螺旋电感的低噪声放大器三维结构

图14给出了仿真结果。增益S21、输入反射系数S11、反向隔离S12、输出反射系数S22和噪声NF分别为14.35dB(＞10dB)、-15.63dB(＜-10dB)、-44.7dB(＜-20dB)、-24.43dB(＜-10dB)和2.99dB(＜4dB)。可以看出，所有的优化结果都符合设计标准。这意味着对5.8GHz LNA系统进行芯片封装协同设计是可行的。