基于FLUENT 的离心式压缩机内部流场的数值模拟研究

2018-11-14唐美玲

沈阳工程学院学报（自然科学版） 2018年4期

关键词：扩散器蜗壳静压

张岳，唐美玲，张凯

（沈阳工程学院a.能源与动力学院；b.学报编辑部，辽宁沈阳 110136）

1 建模及数值求解

1.1 流体流动遵循的控制方程

1）连续性方程

连续性方程也称为质量守恒方程，流体流动的连续性微分方程如下：

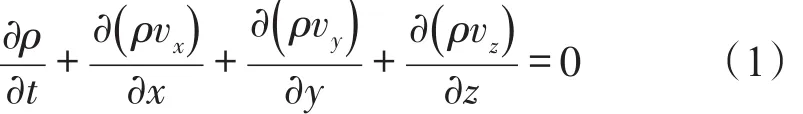
2）动量守恒定律

由流体粘性方程得到的直角坐标系下的动量守恒方程，称为N-S方程。

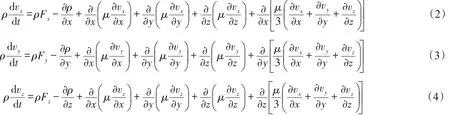
3）能量守恒定律

能量守恒方程式：

1.2 计算模型的建立

利用solidworks建立一个单级离心式压缩机的三维模型，如图1所示。

利用Gambit进行网格划分如图2所示。

所建立的模型包含4部分：压缩机进口、叶轮、无叶扩压器、蜗壳。压比为1.42，进口流量为3.957 m³/min，电机转速为42 000 r/min，流体介质为空气。在建模的过程中，确定进口D0，轮顶间隙取0.3 m。因为研究对象是小流量单级离心压缩机，所以选定的b2D2比较小。扩压器采用等宽无叶扩压器，出口直径为1.5D2。蜗壳采用偏心圆蜗壳。

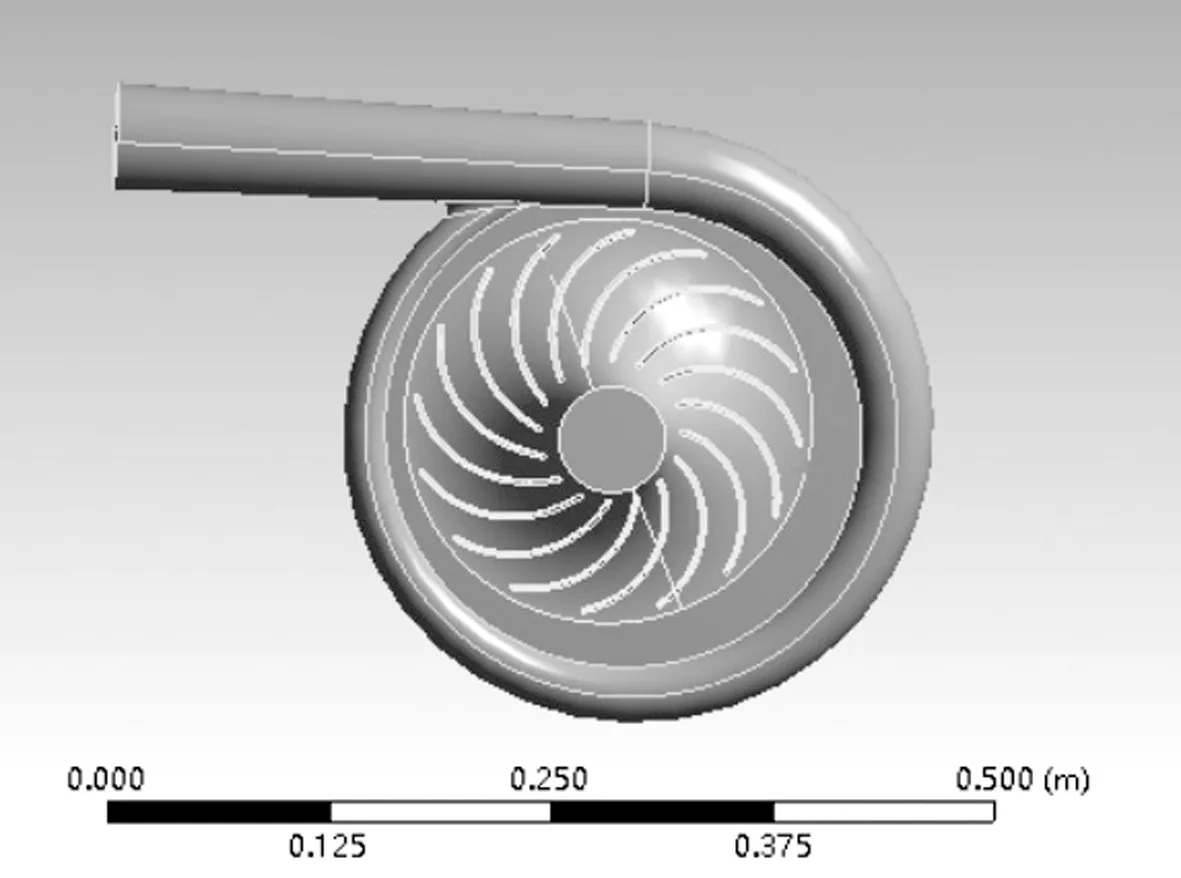
图1 三维模型

图2 网格划分

1）边界条件设定

①进口边界条件：静温为273 K，进口质量流量为0.08 kg/s，进气速度方向为轴向。

②出口边界条件：静压为144 000 Pa。

③壁面边界条件：所有转动壁面（如叶轮叶片表面）的转速n=42 000 rpm，其他壁面转速为0。

2）控制参数的设定

参数设置的基本条件为定常流动、三维、隐式、采用分离式求解器。不考虑质量的影响，其湍流模型是k-ε模型，方程中的系数为默认数值。

①流体的属性：流动介质是空气。

②定义参考系：fluid定义成转动的参考系，将fluid中Rotation-Axis Origin值设置成（0,0,0），将Rotation-Axis Direction的值设定为（0,0,1）；将lun定义为固定坐标系，Rotation-Axis的值设定为（0,-140,0），将Rotation-Axis Direction的值设定为（0,0,1）；将Speed设为42 000 rpm。

③进口及出口的边界条件：把进口Inlet设置成pressure-inlet，进口压力为101 154 Pa；把出口Outlet设置成pressure-outlet，出口压力为144 000 Pa。

④速度的定义：将Translational Velodty的值设定为（0,0,0）。

2 数值计算结果分析

全局残差曲线如图3所示。

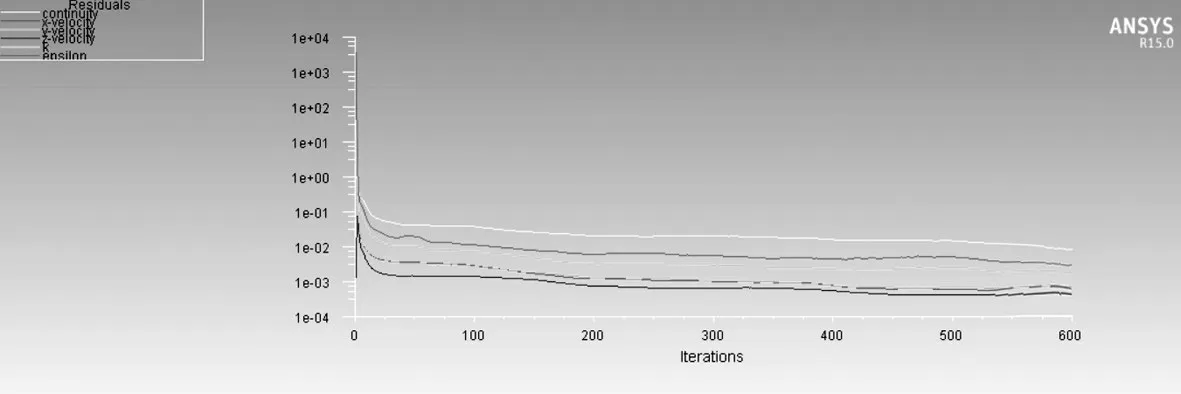
图3 全局残差曲线

从图3中可以看出，经过600次迭代后，剩余值逐渐减小，全局残差减少了3个数量级，符合收敛准则，可以认为是收敛。

2.1 流场分析

压缩机内部静压分布如图4所示。

图4 压缩机内部静压分布

静压呈圆周方向变化，其静压最大值在蜗壳的出口，静压最小值在叶轮非工作面的入口处。压缩机内部静压分布按着圆周方向进行周期变化，可以认定离心式压缩机的边界条件在设计中是较为合理的。在压缩机入口部分和叶轮流动路径的大部分流动区域中，空气在流动时沿着预计气流的流动方向，流动性更加合理。从叶轮到扩散器的空气流量是不均匀的，并且压力变化更明显。扩散器后部的压力稳定地向蜗壳散开，并且蜗壳扩散管中的压力再次增加。

速度矢量图如图5所示。

在旋转叶轮的影响下，气流从单一的轴向流动变为径向、轴向和周向复合流动。离心力的影响和流道内空气流动造成的间隙增大了叶轮内空气流动不均匀趋势。由图5可以确定，前盖板入口流场处存在一个分布规律的逆流区，叶轮通道内的流动严重影响下一步扩散器内的流动。在无叶片扩压器中，无叶片诱导流动方向，速度矢量的圆周分布不均匀。在叶轮出口处空气流速达到最大，然后流到扩散器入口处，经过轮盖侧，速度会逐渐降低，气流从扩散器腔室流动到蜗壳处，速度分布变得不规律，其径向速度稳步下降。

图6为湍流强度等值线。在叶轮流动路径中，湍流强度的变化沿着流线方向逐渐变大。在同一截面上，在叶轮出口和通道中，吸入表面比压力表面稍强，射流梯度的增大使射流尾部的变化更加明显。在扩散器通道的入口处，叶轮射流现象根据尾流产生的影响，其湍流强度向出口处逐渐增大，但湍流强度的增大趋势逐渐减低。由于蜗壳内部湍流强度很小，气流的表现较为稳定。

图6 湍流强度等值线

图7 全压云图

图7 为全压云图。由图7可以看出，流场中总压力的最大值出现在离心式压缩机的叶轮出口和蜗壳出口处。由于叶轮驱动流体高速旋转，所以在叶轮出口处达到最大动压。然后通过扩散器，蜗壳内通流面积变大，会出现涡旋运动导致能量消耗使损失增加，总压力出现下降的现象。蜗壳内流动的气体使管路膨胀，空气流速缓慢下降，转变为压能并逐渐增大，机内全压在圆周方向上呈对称分布。在叶轮入口处及其流道区域内，全压变化稳定。沿着气流流动的方向，压力升高的速度变得更平稳。因此，可以认定流场内的流动相对平稳。

2.2 计算与试验结果分析比较

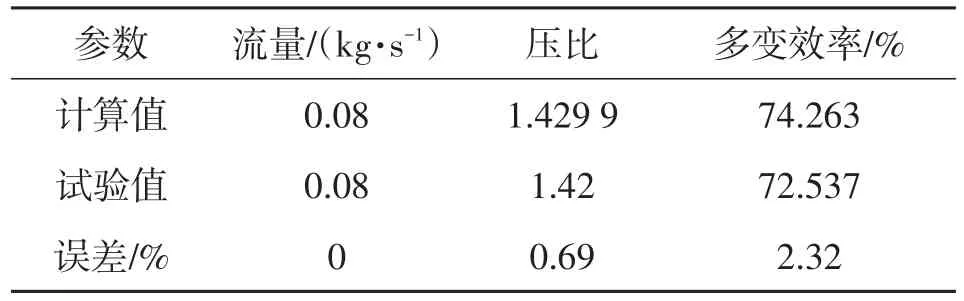
表1 数值计算结果与试验结果的比较

数值计算结果及试验所获得的性能参数如表1所示，误差都不超过3%，且通过数值计算得到的模型性能参数高于测试结果。高参数是因为设计的数值模型忽略叶轮及扩散器中间的间隙，还未考虑到叶轮泄漏及叶轮产生的阻力损失。一般而言，容积损失系数在0.01～0.02范围之间便可，而叶轮阻力损失系数在0.02～0.04范围内也满足条件，流量系数较小的叶轮产生的容积损失及叶轮阻力损失会增加相应比例。可以看出，模型的多变效率比测试值高出约2个百分点左右。因此，数值模拟结果能真实反映模型内部流场的实际情况。