一类特殊矩阵的特征值

乌仁其其格

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 预备知识

定义1.1[1]设A是n阶方阵，若存在数λ和n维非零向量x，使关系式Ax=λx成立，则称数λ是方阵A的特征值，非零向量x称为A的属于特征值λ的特征向量.

定义 1.2[1]的特征多项式，它是以为λ未知数的一元n次多项式，也记为 f(λ).称 |λE-A|=0 为 A 的特征方程.

定理 1.1[1]设 n 阶方阵 A 的特征值为 λ1,λ2,λ3,…,λn，则：

2 主要结论

定理2.1 反对角矩阵

证明 用数学归纳法，

λ2=c2，解得 λ1=c，λ2=-c

假设 n=2k-2，时

得 λ1=c，(k-1 衙） λ2=-c(k-1 重)成立.

得，λ1=c，（k重）λ2=-c,（k重）成立.

定理2.2反对角矩阵

证明用数学归纳法，

(λ-c)(λ2-c)=0，解得 λ1=c,(2 重) λ2=-c

假设 n=2k-1，时

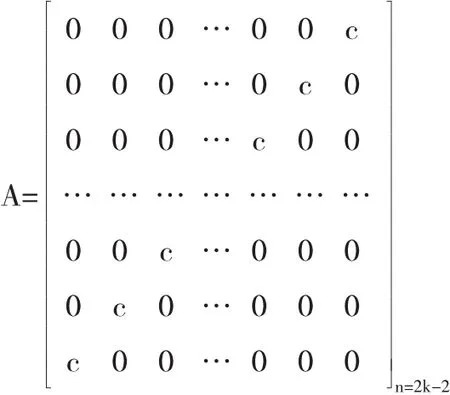
从 |λE-A|=0，得(λ-c)k(λ+c)k-1=0，

得 λ1=c,(k重) λ2=-c(k-1重)成立.

则A的特征方程为|λE-A|=0

A的特征多项式为：

解(λ-c)(λ+c)(λ-c)k(λ+c)k-1=0 得，

得，λ1=c，（k+1重）λ2=-c,（k重）成立.

推论2.1反对角矩阵

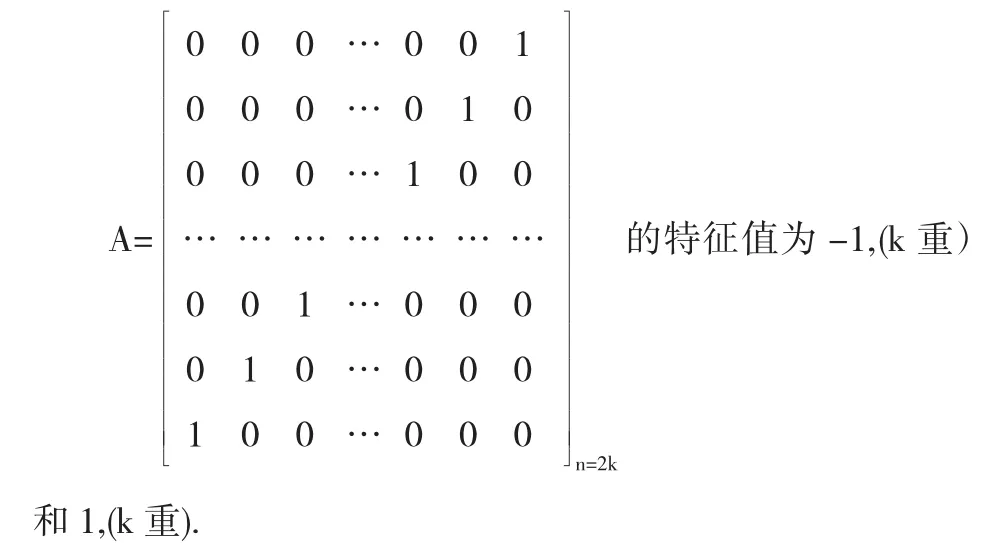
推论2.2反对角矩阵和1(k+1重).

定理2.3设n阶方阵

证明由定理1.1[1]和定理2.1可知显然成立.

定理2.4设n阶方阵

证明由定理1.1[1]和定理2.1可知显然成立.