基于斜交角的多片梁式斜交桥力学性能分析

□□

(中铁十七局集团 第五工程有限公司，山西 太原 030032)

引言

随着社会的不断发展中，一些现有道路越来越不能满足人们日益增长的交通需求。为解决人们的出行需要，需要在现有道路基础上新建或者改扩建公路项目以疏解交通。但在桥梁设计中，由于周围环境条件的限制，同时为了满足线形需要，有时不得已需设计成斜交等复杂形式的桥梁结构。装配式预应力混凝土T梁桥受力明确且构造简单，是中小型桥梁设计时所采用的重要形式之一，而一旦将正交的T梁桥变成斜交的T梁桥，其受力性能将明显不同于直线桥，由于斜交角的存在，受力就会发生较大变化，造成各腹板受力不一致，同时引起支座反力的变化等。

对比已有的斜交T梁桥和正交T梁桥的病害情况，它们之间存在的典型病害情况有较大不同，究其原因，主要是由于它们受力不一致造成的。本文以山西平榆高速公路上不同斜交角度T梁桥为研究背景，采用有限元法分析斜交角度对预应力混凝土T梁桥力学性能的影响，以期为混凝土T梁桥工程设计及维修加固提供参考。

1 工程概况

山西某高速公路桥梁为装配式预应力混凝土T梁桥，施工图纸采用部颁通用图。选取30 m简支T梁为研究对象，桥面宽13.5 m，由6片梁组成，梁高2 m。预制主梁及横隔梁、湿接缝、封锚端、桥面现浇混凝土均采用C50；桥面铺装采用沥青混凝土，设计荷载为公路一级。

主要采用的参数：计算跨径L=28.9 m；弹性模量E=3.45×104MPa；支中截面惯矩IC=0.574 m4；跨中截面面积AC=1.004 m2；跨中截面惯矩IC=0.461 m4；支点截面面积AC=1.430 m2。

2 计算模型

分别建立斜交角为0°、15°、30°及45°的四种模型，以分析斜交角度变化对斜梁桥受力性能的影响。四种模型中均设置了5道横隔板，支座采用弹性支承，简化为简支体系，且考虑桥面板的作用，考虑活载的效应，桥面偏载设置3个车道的汽车荷载。边梁考虑混凝土栏杆的质量，考虑桥面铺装的二期恒载。采用承载能力极限状态计算公式，自重工况(1.200)+桥面铺装(1.200)+预应力(1.200)+栏杆(1.200)+汽车(1.400)。

3 实体模型计算分析

为了分析不同斜交角度对斜交桥主梁受力性能的影响，本文通过分析支座反力、斜交桥最大挠度、弯矩、剪力等力学性能斜交角度变化的规律。

3.1 斜交T梁支座反力分析

支座反力随斜交角度变化规律见图1和表1。

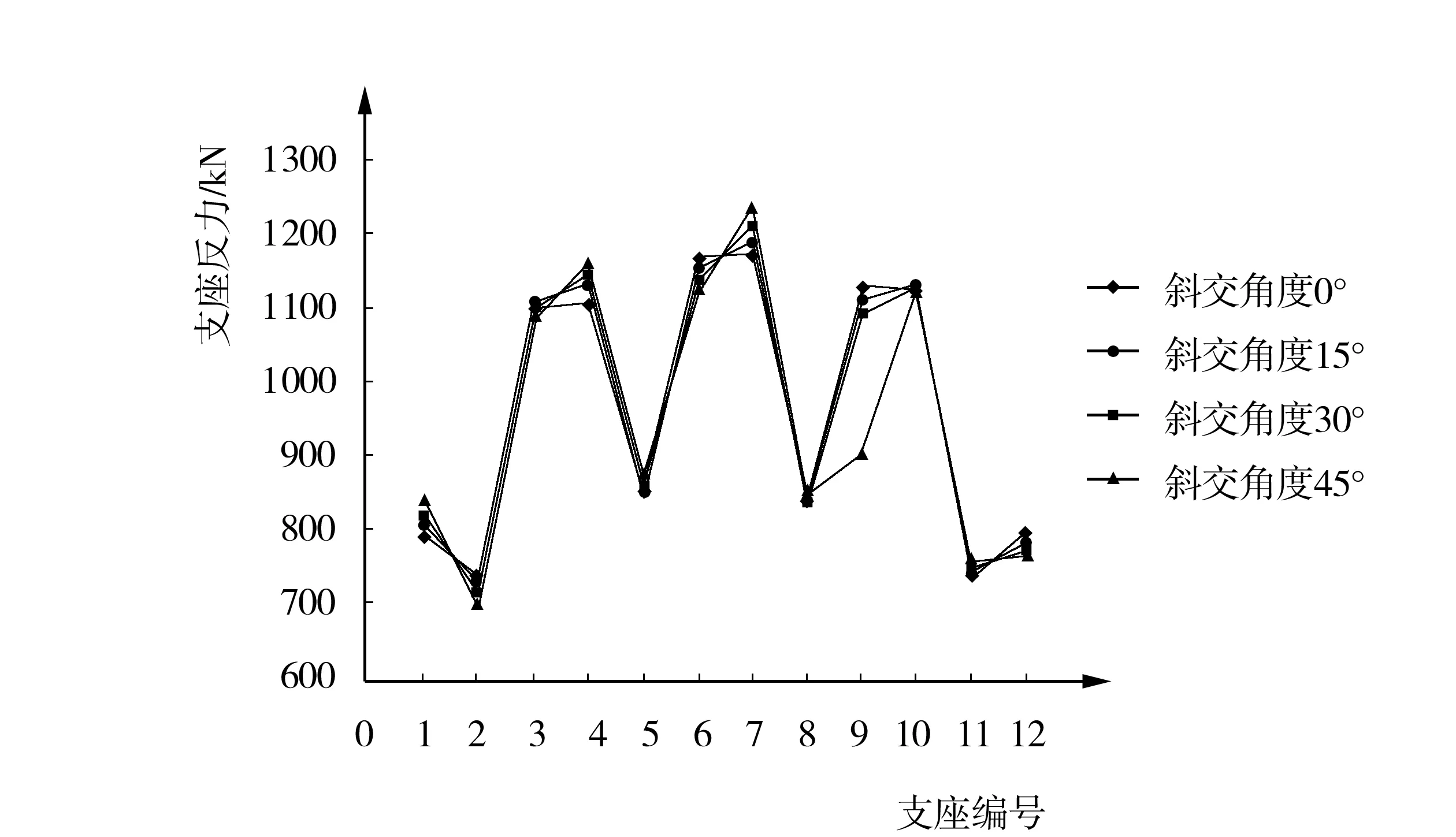
图1 支座反力随斜交角度的变化规律

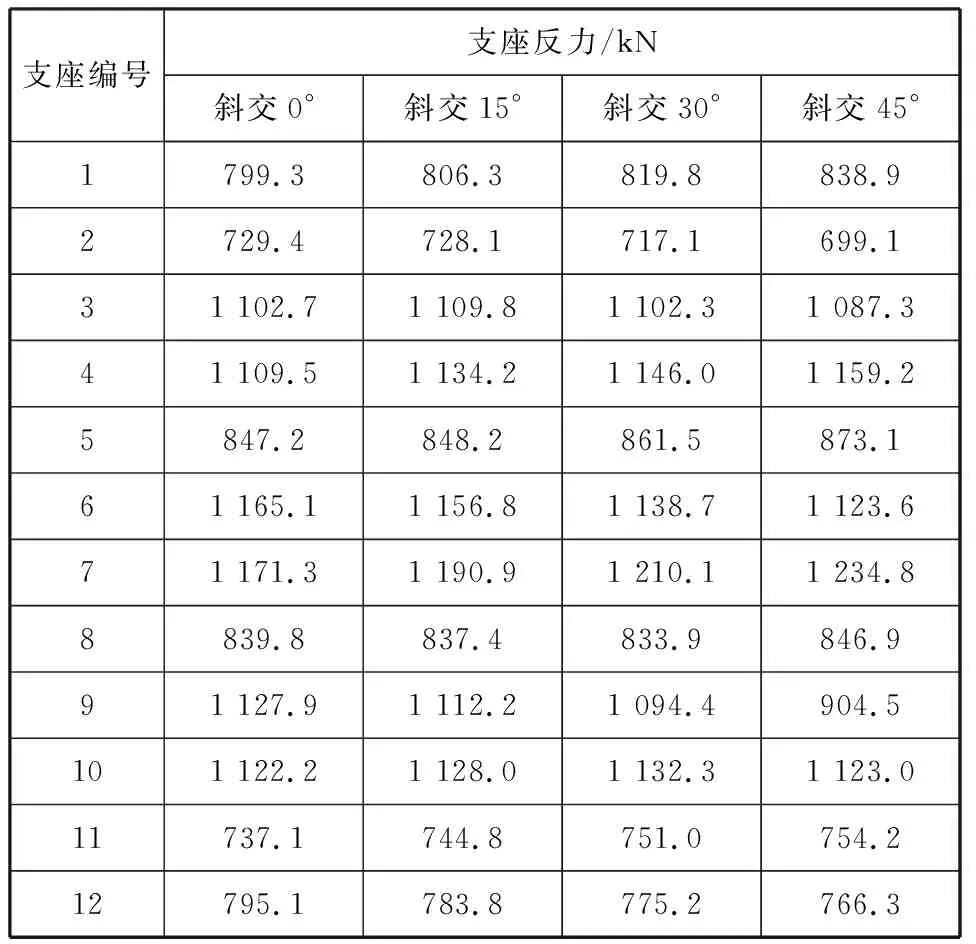
支座编号支座反力/kN斜交0°斜交15°斜交30°斜交45°1799.3806.3819.8838.92729.4728.1717.1699.131 102.71 109.81 102.31 087.341 109.51 134.21 146.01 159.25847.2848.2861.5873.161 165.11 156.81 138.71 123.671 171.31 190.91 210.11 234.88839.8837.4833.9846.991 127.91 112.21 094.4904.5101 122.21 128.01 132.31 123.011737.1744.8751.0754.212795.1783.8775.2766.3

由图1可知，斜T梁支座反力的变化规律基本类似，0°(即正交桥)斜交角时，支座反力变化规律与15°、30°、45°时的支座反力变化规律大致相同，即斜交角度的变化对支座反力变化趋势的影响较小，但对于支座反力的具体数值有明显影响。

为了研究斜交角变化时支座反力的具体变化情况，本文在顺车道方向选取两片边梁的支座反力进行研究，如图2所示。

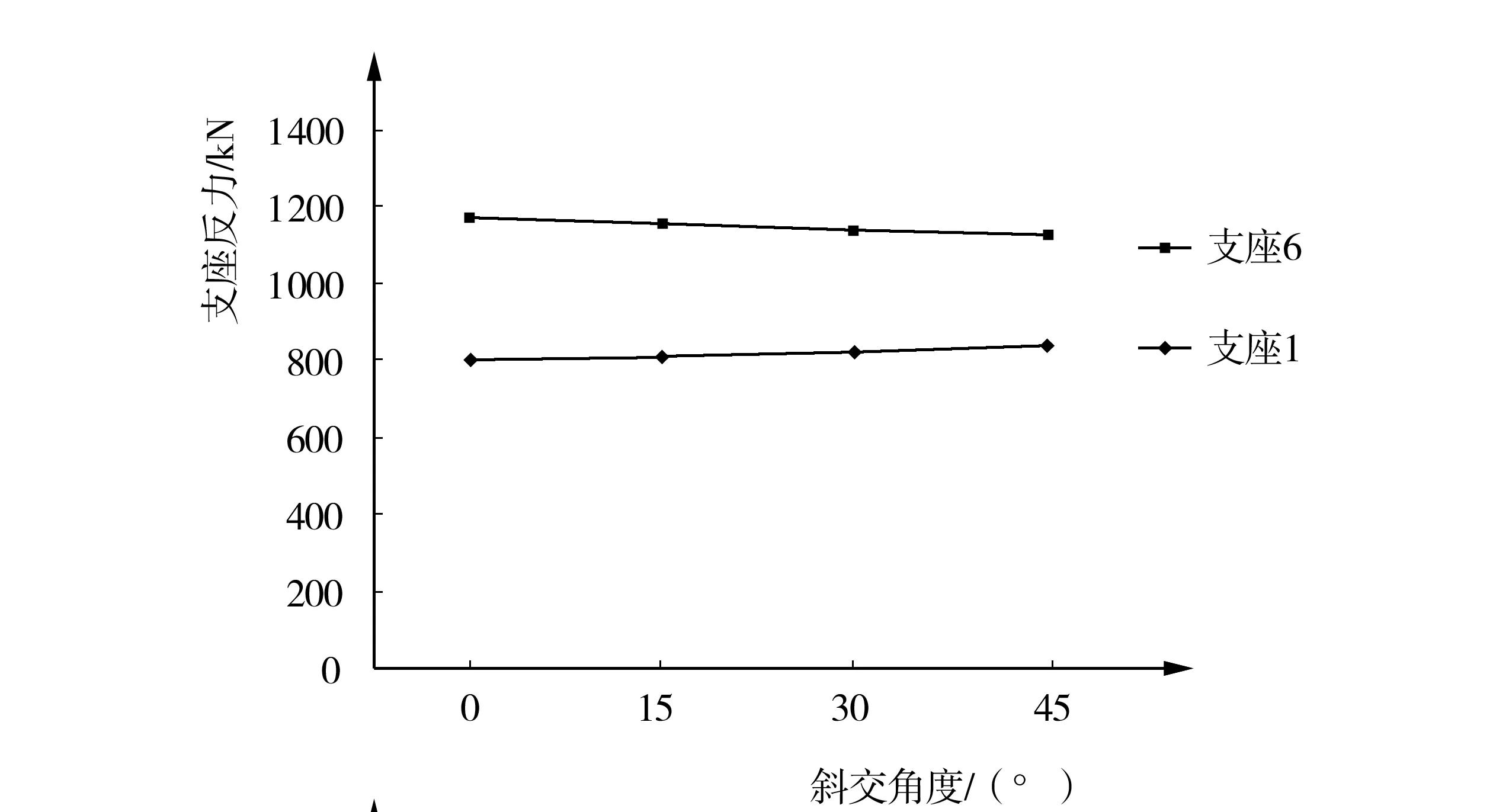
图2 1号和6号支座的支座反力随斜交角度的变化

由图2可知，在顺车道方向，钝角区支座6的支座反力明显大于锐角区支座1的支座反力，二者数值差距达50%。另外，锐角区支座1的支座反力随着斜交角度的增加而逐渐增大，斜交角从0°增加到45°时，支座反力增加4.95%；钝角区支座6的支座反力随着斜交角度的增加反而逐渐减小，斜交角从0°增加到45°时，支座反力减少3.69%。

3.2 斜交角度对最大弯矩的影响

为了研究斜交角度对弯矩的影响，本文选取斜交桥具有代表性的最大弯矩值进行分析，如图3所示。

图3 斜交角度对最大弯矩的影响

由图3可知，斜交桥斜交角度的变化对桥梁的最大弯矩数值有影响。从整体上观察，随着斜交角度的增加，最大弯矩值呈逐渐增大的趋势，但增长趋势趋向于逐渐变缓，其中0°到15°增长率为0.9%，15°到30°增长率为0.4%。因此，斜交角度的变化会对斜交桥的最大弯矩值产生影响，随着斜交角度的增加，最大弯矩值逐渐增大，但是增长率的变化整体较低，对桥梁的最大弯矩影响并不明显。

3.3 跨中挠度随斜交角的变化规律

在模型建立过程中，按照实桥的参数布置预应力钢束，施加荷载以后，桥梁产生上拱度，通过提取结构中的最大挠度值(见表2)，发现随着斜交角度的变化，在排除偶然因素影响的情况下，结构的最大挠度值基本保持不变，因此，斜交角度的变化基本不影响结构的挠度。

表2 最大挠度随斜交角度变化情况

3.4 斜交角对支点剪力的影响

斜交角度的变化，会引起结构支座反力的变化，对结构支点处的剪力也有一定的影响。单从提取的最大剪力数值来看，随着斜交角度的变化，结构的最大剪力数值基本没有变化，但最大剪力出现的位置逐渐向钝角一侧偏移(见图4)，锐角处剪力数值逐渐减小。

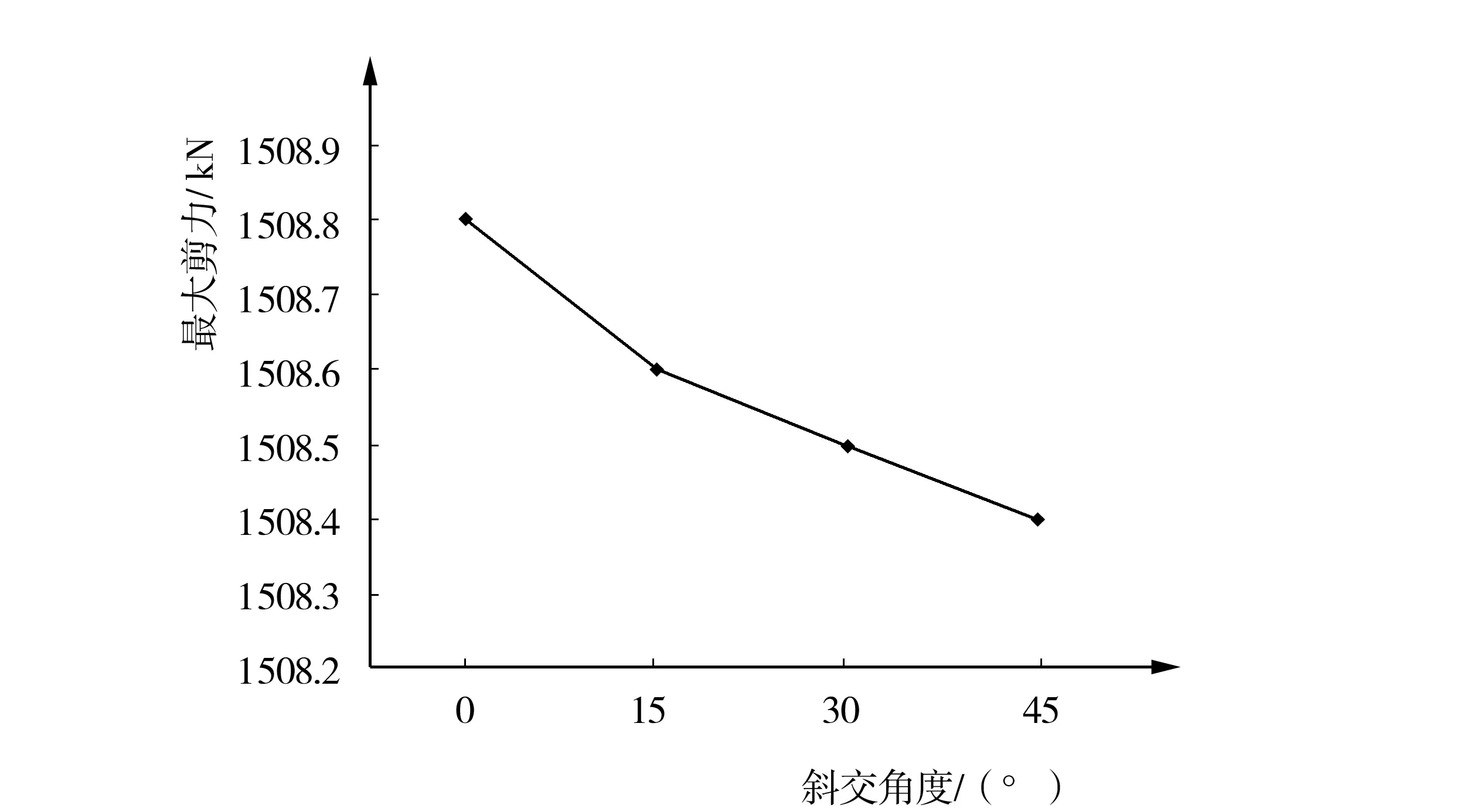
图4 斜交角度对最大剪力的影响

4 结论

通过本文的计算分析，可得出以下结论：

4.1 在荷载作用下，支撑边支座反力分布不均匀，钝角侧增大，锐角侧减小，顺车道方向边梁钝角侧的约束反力同样分布不均匀。

4.2 在钝角处出现较大的剪力，最大剪力和最大弯矩向钝角方向靠拢。

4.3 斜交角度的变化对结构的挠度影响较小，可忽略不计。

4.4 斜交T梁桥中，钝角处支承反力较大，宜采用刚度较大的支座，以增强结构耐久性。同时，需考虑在钝角区上部结构中加密钢筋，以承受荷载。