网格对声爆近场预测影响的数值研究

马博平, 王刚, 雷知锦, 叶正寅

(西北工业大学 航空学院, 陕西 西安 710072)

声爆的抑制问题是新一代环保型超声速客机研发过程中亟需解决的关键技术瓶颈之一[1]。精确地评估超声速客机飞行时地面上感受到的声爆噪声水平是通过低声爆设计降低声爆的先决条件。因此,声爆的预测问题一直是全球航空航天研究机构关注的热点之一。2008年,美国航空航天管理局(the national aeronautics and space administration,NASA)发布了用于声爆近场预测技术验证与确认的多组标准算例,并组织了研讨会论证超声速客机近场声爆预测技术的发展状况与未来趋势[2]。在此基础上,美国航空航天学会(American Institute of Aeronautics and Astronautics, AIAA)又分别于2014年和2017年组织了第一、二届国际声爆预测研讨会(The 1stand 2ndSonic Boom Prediction Workshop, SBPW-1[3]、SBPW-2[4-5]),并发布了更加系统的测试算例,包括中国在内的多国学者参会交流了其在近场和远场声爆预测方面的最新进展。

主流的声爆预测方法分为2步:首先通过风洞实验或计算流体力学(computational fluid danymics,CFD)方法计算飞行器周围较小范围的过压(over-pressure)分布,再以此为输入根据Whitham[6]和Hayes[7]发展的准线性理论或非线性Burgers方程[8]计算地面声爆波形,最后,计算地面声爆的感觉噪声级(PLdB)。因此,提高近场声爆的预测精度是进行全场声爆预测的关键。

近场声爆预测时往往需要考虑超声速流动特有的一些特点以便保证预测结果的可靠性,这其中就包括特殊的网格生成技术。国外针对近场声爆预测的网格生成技术已有一些研究。Cliff 和 Thomas在其研究中分别使用了结构网格和各向同性非结构网格[9]。Choi,Alonso和van der Weide在流场中压力梯度大的区域使用了各向同性自适应网格技术,在一倍机体以内表现出良好的效果[10]。Carter等研究了非结构网格分辨率对声爆近场预测的影响,并指出采用沿来流马赫角对齐的各向异性网格可以显著改善计算结果[11]。Campbell等对上述方法进行了验证与确认[12]。Meredith在其Shaped Sonic Boom Demonstrator(SSBD)项目研究中在笛卡尔坐标系下采用了嵌套网格技术及沿激波角对齐的网格策略,取得了良好的效果[13]。Laflin等在模型周围采用自适应各向同性网格,在此之外则采用沿来流马赫角对齐的结构网格捕捉流场激波,二者之间通过插值实现流场变量的传递,由此提出了一种对于复杂构型快速网格生成方法[14]。

国内对于这方面的研究相对较少。冯晓强采用与文献[11]实质相同的混合网格方法使用CFD分析得到的近场压力分布代替原始的F函数和等效截面积分布作为匹配目标值,提出了改进的F函数方法[15],并在此基础上基于线化理论SGD(seebass-george-darden)反设计方法对声爆/气动一体化设计方法进行了研究,但由于计算资源的限制,其采用了楔形网格进行CFD计算[16]。徐悦等采用马赫锥构型的结构化网格研究了黏性对声爆近场预测结果的影响[17]。王刚等采用与文献[11]一致的非结构混合网格研究了其自研求解器对于声爆标模近场声爆预测的可靠性及精度[18],在此基础上研究了数值离散格式和是否考虑黏性对近场声爆预测结果的影响和以此为输入得到的远场波形的差异,并定性分析了其对人的感受性的影响[19]。

从现有研究结果来看,目前国外学者针对网格量和网格拓扑结构对近场波形的影响开展了一系列的研究工作[20],但对结构和非结构网格、不同网格类型和网格分布等因素对于近场声爆预测结果的影响缺少系统研究。为此,本文选取旋成体双锥和带翼锥体构型采用数值方法分别就网格对齐方式、网格类型、网格生成方法和分布对声爆近场预测的精度的影响进行了分析和研究。最后,使用实验数据齐全的LM1021标模验证了所得到的结论。

1 数值方法

本文使用自研非结构混合网格复杂流场模拟程序HUNS3D[21]数值求解三维Euler/雷诺平均Navier-Stokes方程来实现近场声爆的数值预测。

直角坐标系下,采用Spalart-Allmars(SA)一方程湍流模型[22]封闭的积分形式的三维RANS方程为:

(1)

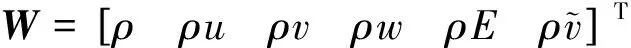
在HUNS3D中,流动控制方程通过格心格式有限体积法进行离散。对流通量Fc可以采用包括ROE[23]、AUSM(advection upstream splitting method)系列格式[24]、熵守恒格式(entropy consistent,EC)[25]在内的多种迎风型格式和中心格式JST(jameson-schmidt-turkel)[26]进行数值计算。在超声速流动数值模拟中上述迎风格式均需要和Venkatakrishnan斜率限制器[27]配合使用以保证总变差减小(TVD,total-variation-diminishing)特性。

在HUNS3D,黏性通量Fv采用中心格式进行离散;湍流雷诺应力可以选用包括SA一方程模型、Menter′s MSST(shear stress transport)两方程模型[28]和DES(detached eddy simulation)模型等湍流模拟方法进行封闭。时间离散采用LU-SGS(lower-upper symmetric Gauss-seidel)方法,该算法利用矩阵的LU分解避免了复杂的矩阵求逆运算,具备较高的计算效率。

2 网格生成方法及其影响

2.1 网格对齐方式的影响

声爆是飞行器在超声速飞行过程中产生的特定声学现象,其本质是超声速飞行时飞行器周围产生的激波,当其传播至地面时就形成了声爆。因此,要准确的对声爆进行预测,关键在于精确的捕捉流场中产生的激波信息。对于定常超声速流动,激波角μ计算公式为

μ=sin-1(1/M)

(2)

式中,M为来流马赫数。与传统正交网格相比,马赫锥构型的网格计算时相对前者更能够减小计算耗散,因而可以更为精准的捕捉激波信息,进而能够更为精准的预测声爆。

本文基于双锥构型研究网格对齐方式的影响。双锥模型如图1所示,锥体长度为0.050 8 m(L=2 inches),沿轴向半径分布如公式(3)所示, 风洞试验数据取自Carlson、Mark 和Morris于1965年在NASA兰利研究中心4×4英寸超声速风洞的实验结果。

(3)

本文数值模拟选取马赫数为2.01,迎角0°,湍流模型为SA湍流模型,雷诺数为7.38×106/m。本算例中,分别使用了3套非结构混合网格,其拓扑结构示意图如图2所示。模型壁面附近圆柱区域采用非结构网格,非结构网格对复杂外形具有适应性强、划分简单的优点,在外部拉伸区域采用结构化网格,以便更好的捕捉激波。3套网格除拉伸区域倾斜角度外其他因素一律相同,图中ψ表示网格拉伸方向与来流夹角,3套网格夹角分别为μ-5,μ和μ+5。其中,沿马赫角对齐(ψ=μ)的网格示意图见图3。所有网格的边界层第一层网格高度均满足y+小于1,边界层数40层,增长率1.21。网格节点数8 923 645,单元数10 303 712。

图1双锥模型示意图 图2 双锥模型网格拓扑示意图 图3 双锥模型网格示意图

计算结果如图4所示,在距离模型较近区域(h/L=1)处可以看出不同锥角计算结果基本完全重合,表明此时锥角对于捕捉到的激波形状并没有显著影响,随着距离模型增大,到h/L=5时,由于锥角不同产生的差异逐渐明显,锥角为马赫角的网格捕捉到的激波峰值和谷值范围最大,其余2组网格捕捉到的波形明显钝化一些。除此之外,锥角为马赫角的网格在x=17处捕捉到的激波上升处也更为迅速。图4c)为h/L=10处的结果,图中除不同锥角网格计算结果外,还对比了实验值。由图可以看出,在离模型较远距离处,使用锥角为马赫角的网格计算得到的波形与实验结果基本完全吻合,于此同时,其余2组计算结果与实验结果均有明显误差,在激波上升处仅有锥角为马赫角网格捕捉到的波形与实验结果完全吻合。由此可以证明,采用马赫锥构型网格由于可以显著减小激波传播时数值耗散,有利于捕捉激波,因而更有利于提高声爆预测的精度。

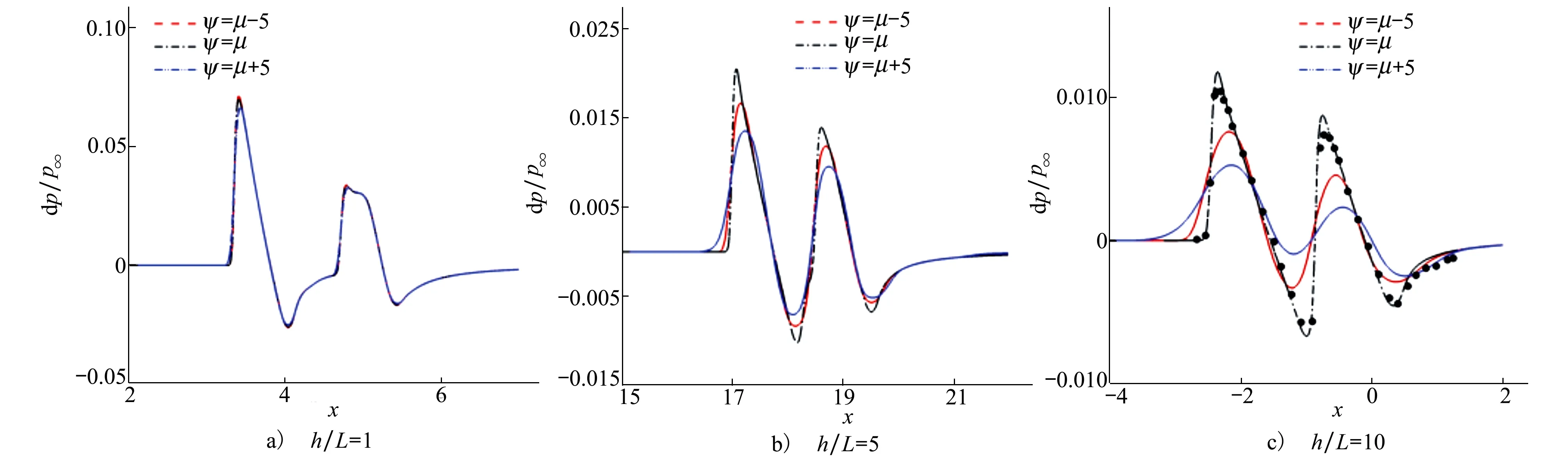
图4 双锥模型h/L=1,5,10处不同锥角近场过压计算结果

2.2 结构和非结构网格的影响

网格是进行CFD流场计算的基础,合理的网格分布是正确模拟一些复杂流动的基本前提。网格主要分为结构网格和非结构网格。结构网格虽然具有可以控制网格拓扑的划分和网格的正交性的优点,但是对于复杂构型来说,网格生成周期长甚至无法生成。而非结构网格则具有很强的描述复杂几何形状构型的能力,易于得到高质量的网格,同时,非结构网格生成过程快速且自动化程度高。

本文选取DWB模型来研究结构网格和非结构网格对声爆近场预测的影响,该模型选自Hunton等[29]于1973年的进行风洞实验。DWB模型为面对称模型,包括1个机身和2个三角翼构型,模型参考长度为0.175 2 m,三角翼前缘后掠角为69°。该布局被广泛用于声爆研究,在第一届AIAA声爆预测会议中被选为测试模型之一。本文DWB构型计算采用的是SA湍流模型,雷诺数为7.38×106/m。

图5 DWB模型、2种计算域及近壁面网格示意图

图5a)～c)所示为DWB模型、计算域示意图。根据拓扑结构可将网格分为模型附近带圆柱区域和不带圆柱区域。所谓圆柱区域,即为网格拓扑中模型附近包裹模型的部分。对于带圆柱区域网格,为减小激波信号传播过程中的耗散,圆柱应尽可能小地包围模型。圆柱区域以外采用马赫锥构型,即网格沿马赫角由圆柱表面往外拉伸,本算例中拉伸部分网格为六面体单元。图5d)～f)分别为采用非结构混合网格近场、带圆柱内场结构网格近场和不带圆柱结构网格近场示意图。网格数据如表1所示。

表1 不同网格类型网格量示意图

图6a)～d)分别不同网格拓扑结构在不同周向角(φ)下近场声爆过压计算结果。由图可以看出,不同网格拓扑结构捕捉到的激波形状均与实验吻合较好,不同结果之间的区别主要在过压峰值处。有圆柱区域结构网格和混合网格计算结果几乎完全一致,这得益于2组网格具有同样的拓扑结构,同时,除圆柱内区域以外,其余部分网格分布也基本相同。对于2组结构网格,无圆柱区域网格计算结果与实验值偏差较大,这主要是由于其在模型附近网格拉伸明显,引入了更大的耗散,如图6c)所示。因此,对于用于声爆近场预测的楔形拓扑结构的网格,用混合网格能够取得更好的效果。尽管带圆柱区域结构网格具有类似的效果,但生成结构网格相较于非结构混合网格需要花费更长时间,因此非结构混合网格可以取得快速高效的效果,应用更为方便。

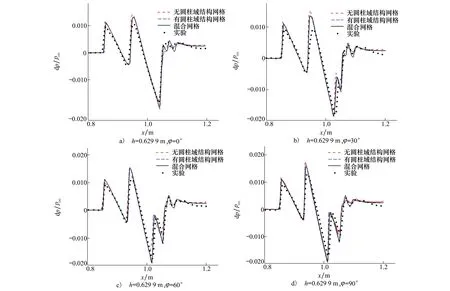
图6 使用结构和非结构网格计算的DWB近场过压预测结果与实验结果的比较

除此之外,由图6a)～d)可以明显看出随着方位角的变化,尾部激波从单个激波演变为多个激波,数值模拟捕捉到的演变程与实验曲线表现的变化规律基本一致。

2.3 网格类型的影响

为研究圆柱区域外网格类型对声爆波形传播的影响,本文在DWB楔形拓扑结构基础上在圆柱区域以外分别使用了四面体、六面体混合网格和全四面体网格,如图7a)～b)所示。其中,四面体、六面体混合网格网格节点数为5 303 747,单元数为8 734 621,四面体混合网格网格节点数为3 172 122,单元数为9 755 505。

图7 DWB模型不同网格类型示意图

图8a)～b)分别为四面体、六面体混合网格和全四面体网格计算得到的DWB构型近场过压结果和实验值在不同周向角下的对比。由图可以看出,六面体混合网格和四面体混合网格计算得到的近场过压结果基本一致,且与实验结果吻合较好,表明在网格量近似的情况下,网格类型对声爆预测的影响有限。

2.4 网格分布的影响

在CFD的实际应用中,计算精度和计算量往往是相互矛盾的关系,当要求提高计算精度时,计算量往往会增大,反之亦然。因此如果可以将网格节点分布到更为流场中更为“合适”的地方,对提高计算效率可能会起到事半功倍的作用。对于本文中采用的马赫锥构型,当模型轴向方向网格点给定后,为探究圆柱体周向和垂直模型轴方向的网格分布对声爆预测的精度影响,本文利用DWB带翼锥体模型分别生成了3套不同分布的网格进行了计算,并将结果与实验值进行了比对,网格分布参数示意图和不同展弦比网格信息分别如图9和表2所示。

图9 网格分布参数定义

表2 不同展弦比网格信息

2.4.1 网格展弦比的影响

图10a)～b)为DWB模型在其中心线下方h=0.629 9 m不同周向角处结果。图中计算都采用HUNS3D在黏性条件下计算,短折线代表网格展弦比为10的结果,点划线代表的是展弦比为4的结果,双点划线代表网格展弦比为1的网格计算的结果,实验测量结果用黑点表示。可以发现,网格展弦比在一定范围内对近场声爆预测基本没有影响。不同展弦比的网格在不同高度不同周向角的条件下捕捉到的激波形状都能够很好吻合,同时,和实验值也吻合很好。但将网格展弦比系数进一步增大时,可以发现网格展弦比对捕捉到的激波峰值有明显影响,见图10c)～d)。

图10 DWB模型不同展弦比网格计算的近场声爆过压预测结果与实验结果对比

2.4.2 周向网格间距的影响

表3给出了不同周向间距的3套测试网格详细信息。

表3 不同周向距离网格信息

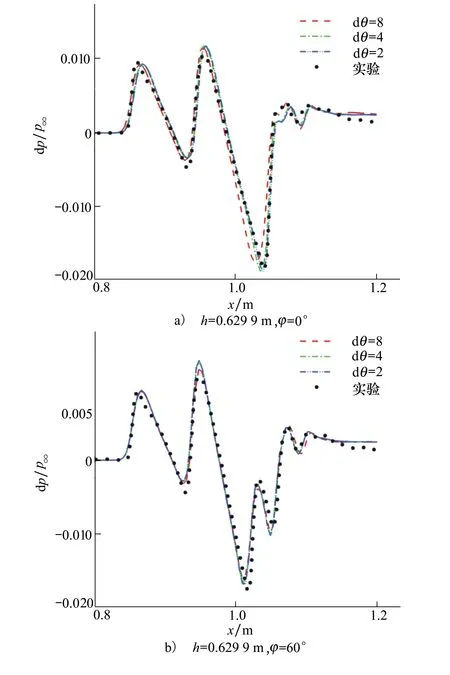
图11 DWB模型不同周向距离网格计算的近场声爆过压预测结果与实验结果对比

图11a)～b)为DWB模型在其中心线下方h=0.629 9 m不同周向角处结果。图中计算都采用HUNS3D在黏性条件下计算,短折线代表网格内部圆柱区域周向角度为8的结果,点划线代表的是周向角度为4的结果,双点划线代表周向角度为2的网格计算的结果,实验测量结果用黑点表示。不同周向角度网格的网格量信息见表3。

可以发现,圆柱区域周向角度对捕捉到的激波“陡峭”程度有明显影响,采用周向角度较小的网格捕捉到的激波形状更为“尖锐”,并且和实验值吻合更好。

以上结果表明,网格展弦比和马赫锥面周向网格间距对流场中激波峰值和激波形状的捕捉有明显影响,使用相对合理的网格展弦比和马赫锥面周向网格间距有利于提高近场声爆预测精度。

3 复杂构型近场声爆预测

3.1 模型和网格生成

为验证前文所述的网格生成策略在复杂构型中的应用效果,本文选取了SBPW-1中作为可选算例的标模LM1021全机方案进行测试。采用带圆柱区域的混合网格拓扑结构,其中圆柱内周向角度为2,远场网格展弦比为1。圆柱区域以外采用沿马赫角对齐六面体网格以便于捕捉声爆传播。

LM1021方案来自美国Lockheed-Martin公司,包括3个发动机短舱和1个V型尾翼。其参考长度为0.568 9 m,实验数据测量条件为来流马赫数1.6,迎角2.3°(模型在网格中已绕前缘点旋转,因此CFD求解中迎角为0°)。此算例中网格节点数为24 805 540,单元数为12 144 918。面网格数目为252 741,附面层33层,第1层高度满足y+小于1。计算采用MSST湍流模型,雷诺数为7.38×106/m。模型及网格详细示意图如图12a)～b)所示。

3.2 计算分析

图13a)～f)为不同周向角下模型正下方h=0.807 7 m处CFD计算得到的LM1021近场过压预测结果结果和实验结果的对比。由图可以看出,CFD计算结果准确捕捉到了LM1021构型流场中复杂的激波系,且与实验测量的演化过程基本一致,表明所采用的网格策略有效。

图12 LM1021构型及网格示意图

图13 LM1021构型CFD计算的近场声爆过压预测结果与实验结果对比

4 结 论

本文使用自研流场求解器对3组典型标模的近场声爆过压分布进行了数值模拟和分析。双锥旋成体模型的算例表明网格对齐方式对声爆近场过压分布具有非常明显的影响,即网格面沿马赫角对齐可以显著提高近场过压预测结果捕捉的精度。DWB模型的算例表明,模型附近采用圆柱区域包裹的结构和非结构网格均能很好地捕捉声爆近场过压预测结果,但非结构网格由于可以快速生成,应用更加方便;马赫锥面方向采用四面体和六面体网格对近场声爆预测精度影响不大;在采用带圆柱区域的混合网格时,网格展弦比和马赫锥面周向网格间距对流场中激波峰值和激波形状的捕捉有明显影响,使用相对合理的网格展弦比和马赫锥面周向网格间距有利于提高近场声爆预测精度。最后,将总结的网格生成策略应用于LM1021全机构型1.42倍机体长度下方近场过压预测,计算结果与实验测量结果吻合良好,验证了其实用性。