多通道鲁棒故障卫星参数估计算法

侯翔昊, 袁建平

(西北工业大学 航天学院, 陕西 西安 710072)

自主交会对接技术是当前在轨服务任务中的关键技术之一[1-2]。尤其是针对故障卫星的在轨服务技术不仅能够再次利用这些空间资源，也可以减少空间碎片，维护太空环境。这类故障卫星由于燃料耗尽或者部件失效导致其成为空间中的一种非合作目标，并且不受控制地在空间中做自由翻滚运动。因此，为了对这类目标进行空间操作，必须对其参数进行预先识别。对故障卫星参数准确识别对进一步的在轨服务操作有着重大意义。由于故障卫星是一种空间非合作目标，其自身并不能提供充分的先验信息，因此目前只能够采用非接触式的测量设备(单目相机、双目相机、LIDAR、激光测距仪等)对其相对姿态与位置进行测量。然而，由于空间环境十分复杂，导致这类基于视觉的敏感器测量精度普遍较低，并且测量信息有限。因此，如何基于这些测量信息对空间故障卫星进行准确且鲁棒的参数识别是目前研究的重点。

基于对目标的测量，文献[3]采用了基于图像处理算法的技术对空间故障卫星进行了参数识别。然而，这类方法局限在图像处理的方法框架之中，并没有考虑目标在空间中的运动学与动力学模型。因此，这类方法计算量大，且估计能力十分有限，一般只能估计目标卫星的相对姿态参数。因此，在目标卫星参数识别任务中，这类方法的理论价值远高于其实际价值。针对这类方法的不足，一些研究者采用视觉测量结果，同时也利用了目标卫星的相对运动学方程来描述其运动特征，从而估计目标卫星的姿态参数。文献[4]利用视觉敏感器的测量，设计了一种基于EKF的姿态估计算法。文献[5]也采用了类似的方法。然而，上述研究针对的目标卫星是合作的航天器。这样，相比于对故障卫星的测量，上述研究中的测量量都是准确且不受空间环境干扰的，因此上述研究所采用的参数估计方法并不考虑算法的鲁棒性与容错性。并且，由于上述研究并没有使用动力学方程，因此对目标卫星的动力学参数无法做出估计。

文献[6]首次采用了目标的运动学方程以及动力学方程来对目标卫星进行建模，同时采用LIDAR视觉系统的测量值作为输入对目标卫星进行参数估计。文献[7-8]采用了相同的测量手段对一个空间失效且自由翻滚的卫星进行了参数估计研究。通过使用目标的运动学方程以及动力学方程，文献[7-8]设计了一种基于EKF框架的参数估计方法对故障目标的位姿参数以及质量参数做出了一体化的参数估计。文献[9]采用了基于单目视觉相机以及LIDAR的测量作为输入，同时使用了基于UKF的参数估计方法对空间故障卫星的位姿参数进行了估计。然而，上述的研究都采用了基于四元数的传统运动学模型以及传统动力学模型。在这种情况下，姿轨耦合现象并没有得到考虑。因此，上述方法只能够用于轻度姿轨耦合的参数识别任务中。

为了解决上述由于采用传统方法建模而产生的问题，一些学者采用了对偶四元数来对目标的运动学以及动力学进行建模。与传统建模方法不同，对偶四元数将姿态参数与位置参数同时考虑，并将这两者结合在一起。这样，采用对偶四元数对目标的运动学与动力学方程进行建模就能够考虑姿轨耦合效应，同时还使得目标的运动学与动力学模型表达更为简洁与紧凑。不仅如此，由于对偶四元数与四元数的数学表达相似性，对偶四元数在应用中也更容易被接受。文献[10]采用了基于对偶四元数的运动学方程对空间目标的位姿参数进行了估计。文献[11]采用了基于误差四元数的对偶四元数运动学模型，并设计了基于EKF框架的参数估计算法对空间目标的参数进行了一体化估计。针对空间中的复杂环境以及为了对空间非合作目标作出全面的参数估计，文献[12]采用了基于矢量对偶四元数的相对运动学与相对动力学方程，对空间非合作目标的位姿参数与质量参数做出了自适应估计，具有一定的鲁棒性。然而，上述研究只针对单一测量敏感器设计了参数估计算法，当复杂空间环境使测量敏感器较长时间内处于失效环境中或者某一测量敏感器损坏时，上述研究中的参数估计算法并不能得出有效的参数估计结果。

基于上述研究的优点与不足，本文提出了一种针对空间中的失效卫星的多通道鲁棒参数估计方法(DVQ-REKF)。首先，本文采用新型的矢量对偶四元数对目标的运动学与动力学进行建模。其次，本文所设计的服务航天器采用2个相互独立的单目相机以及公用的激光测距仪来测量故障卫星的相对姿态与距离信息。针对空间环境尤其是复杂的空间光照环境，射线环境可能对CCD相机造成的干扰甚至损毁，本文采用2路相互独立的单目相机测量结果，当其中一路测量信息失效时，另外一路测量信息仍然能够提供可靠的测量信息。同时，考虑到激光在空间中的稳定特性，本文只采用一路激光测距信息，从而有效降低服务航天器的能耗以及成本。基于上述模型与测量信息，服务航天器首先进行相互独立的基于EKF框架的单通道目标参数估计(DVQ-EKF)。之后，采用联邦滤波器作为多通道信息融合算法，本文设计了多通道鲁棒参数估计方法(DVQ-REKF)，从而对目标进行鲁棒参数估计。基于本文所设计的多通道鲁棒参数估计方法(DVQ-REKF)，故障卫星的位姿参数以及质量参数均能得到准确且鲁棒的估计。

1 四元数与矢量对偶四元数

1.1 四元数

四元数具有如下形式：

q=(q0,q1,q2,q3)=q0+q1i+q2j+q3k

(1)

式中,q0是标量部分,q1i+q2j+q3k是矢量部分。其共轭表示为:(q0,-q1,-q2,-q3)。

同时,四元数与实数域的映射关系表示为:[·]:Q4→R4。在这种映射定义下,四元数叉乘可以定义在实数域内:

[a×b]=[a×][b]

(2)

类似的,四元数内积可以定义为:

[ab]=[a]L[b]

(3)

式中:

并且

1.2 对偶四元数与矢量对偶四元数

对偶四元数有如下形式:

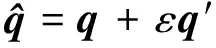
(4)

式中,q以及q′均为四元数,并且对偶运算符ε2=0,ε≠0。

如果只采用四元数的矢量部分,那么矢量对偶四元数可以表示为:

(5)

1) 矢量对偶四元数加法:

(6)

2) 矢量对偶四元数乘法:

(7)

3) 矢量对偶四元数共轭:

(8)

4) 矢量对偶四元数交换:

(9)

其余有关矢量对偶四元数的运算可以参考献[12]。

2 基于矢量对偶四元数的运动学与动力学模型

2.1 模型综述

图1展示了服务航天器以及空间中自由翻滚的故障卫星模型。{I}是惯性系。{B}是故障卫星的本体系,坐标原点为故障卫星的质心。不考虑服务航天器的自身尺寸,服务航天器上有2个相互独立的单目相机以及一个激光测距仪。假设{B′}是抓捕位置坐标系,坐标原点位于抓捕位置几何中心。由于目标是我方故障航天器,抓捕位置的安装矩阵已知,因此,假设且{B}与{B′}平行。抓捕位置的几何中心与目标质心之间的位移为ρ。

{B}相对于{I}的姿态四元数为:qB/I,{B}与{I}相对距离为rB/I,{B′}与{I}的距离为rm。同时,本文假设故障卫星相对服务航天器的线速度为v,角速度为ω。

图1 服务航天器与故障航天器模型图

2.2 基于矢量对偶四元数的运动学与动力学模型

由文献[10],并只采用其矢量部分,{B}相对于{I}的矢量对偶四元数为:

(10)

同时,定义矢量对偶速度如下:

(11)

由文献[12],并取其矢量部分,基于矢量对偶四元数的运动学方程可以表示为:

(12)

由文献[12],采用误差矢量对偶四元数的运动学方程为:

(13)

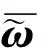
由于只有当误差姿态为180°时,误差四元数才会出现奇异。而当参数估计算法有效时,误差将远远小于180°。因此,当参数估计算法有效时,可以认为误差矢量四元数不会奇异。

由文献[12],基于矢量对偶四元数的动力学方程为:

(14)

相关运算参考文献[13]。

3 基于矢量对偶四元数的故障卫星容错参数估计算法

本章基于每个单目相机设计了测量正常时独立参数估计算法(DVQ-EKF),根据每个通道的DVQ-EKF输出,进一步设计了多通道鲁棒参数估计算法(DVQ-REKF)。

3.1 测量方程及其线性化

每个单目相机能够获得目标的抓捕点相对于服务航天器的相对姿态测量量,激光测距系统能够获得目标的抓捕点与服务航天器的相对位置,则在同一时刻,每一路独立的测量方程为:

(15)

式中,qm是每一个单目相机测量的相对姿态。rm是激光测距仪测量的相对距离。v是测量噪声,假设其为高斯白噪声,且R=E[vvT]。

由文献[8],qm可以表示为:

(16)

式中

(17)

同时,由图1,可得:

(18)

式中,A(qB/I)是{B′}到{I}的姿态转移矩阵。根据3.1的假设,测量值qm=q。

(18)式可以采用一阶泰勒级数展开为:

(19)

并且

(20)

考虑(19)式、(20)式,观测方程可以表示为:

(21)

定义系统状态为:

(22)

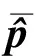
因此,观测方程的线性化形式为:

(23)

3.2 DVQ-EKF设计

基于(22)式的状态,以及(13)式、(14)式,本小节先推导状态方程的线性化形式,继而设计DVQ-EKF。

假设在参数识别过程中,质量参数不变,即:

(24)

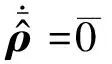
(25)

结合(13)式、(14)式、(24)式、(25)式,系统状态方程为:

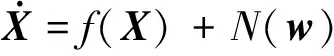
(26)

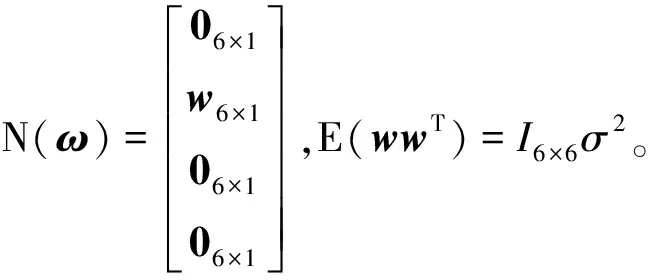
因此,线性化后的状态方程为:

Xk+1=ΦkXk+wk

(27)

式中,Φk≐I+FΔt,Δt为采样时间,并且:

(28)

式中:

(29)

式中:

是过程噪声的强度。

由文献[14]，DVQ-EKF可以设计为:

1) 时间更新:

XK/K-1=ΦkXk-1/k-1

(30)

(31)

2) 测量更新:

(32)

δXk=Kk(Zk-h(Xk/k-1))

(33)

Pk=[I-KkHk]Pk/k-1

(34)

3) 状态更新:

(35)

Xk/k=Xk-1/k-1+δXk

(36)

3.3 DVQ-REKF设计

考虑空间中的复杂环境可能会对单目相机造成干扰,导致测量不准确或者测量失效的问题,本小节设计了多通道鲁棒参数估计算法(DVQ-REKF)。

图2表示了DVQ-REKF的算法结构图。首先,服务航天器分别接收同一时刻每一个独立通道的测量量,并进行双通道相互独立的DVQ-EKF参数估计。之后,参数估计结果输入基于联邦滤波器框架的数据融合系统并进行数据处理,生成经过融合的鲁棒参数估计。

图2 DVQ-REKF结构图

假设Xi,Pi(i=1,2)代表分别表示每一通道的DVQ-EKF参数估计量与其协方差,由联邦滤波器信息分配原理可知,融合后的协方差P以及状态估计X为:

(37)

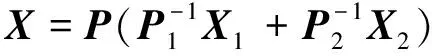
(38)

通过(37)式、(38)式可以发现,当某一通道因为单目相机的测量失效从而导致其DVQ-EKF参数估计出现偏差时,可以通过平衡两个通道各自参数估计的结果,进行信息融合,从而获得更为可靠的多通道鲁棒参数估计。

4 仿真验证

本章通过Matlab仿真验证平台验证了本文所设计的DVQ-EKF以及DVQ-REKF的效果。

同时,假设外界干扰为高斯白噪声,且:

(39)

(40)

分别表示外力对角速度和线速度的干扰。

假设视觉测量系统的采样频率为2 Hz,测量噪声也为高斯白噪声,且协方差为:

R=diag((0.01)I4×4,(0.1)I4×4)m

(41)

待估计参数的初始值如下表设定:

表1 参数初始值

并且,初始化的状态协方差矩阵为:P(0)=I24×24,仿真总时间为T=200 s。

由于复杂的空间环境的干扰,考虑2个单目相机中的一个测量失效或者两者均测量失效的情况。假设复杂环境对测量的影响体现在测量噪声上:对qm的影响为对其附加一均值为0,方差为0.1的白噪声;对rm的影响为对其附加一均值为0,方差为1的白噪声。设置单目相机1的测量失效时间为仿真开始后的第25～第35 s,设置单目相机2的测量失效时间为方针开始后的第60～第70 s,设置2个单目相机均测量失效的时间为方针开始后的第120～第130 s。

图3 单目相机测量失效时DVQ-EKF参数估计误差2-范数 图4 四元数误差仿真结果 图5 相对距离误差仿真结果

图9 故障卫星质心位置误差仿真结果

图10 综合误差2-范数仿真结果

如图3所示，当某一通道测量失效情况发生时，由于DVQ-EKF没有容错机制，因此不能在失效测量的情况下对故障卫星的参数进行独立估计。

图4～图10展示了采用DVQ-REKF对故障卫星进行参数估计的结果。可以看到，由于DVQ-REKF能够分配双通道参数估计的权重，因此，DVQ-REKF能够在测量失效发生时，仍然对故障卫星做出有效的参数估计。图10显示了情况2下，DVQ-REKF的参数估计整体效果。可以看到，在仿真时间为300 s时，该误差的2-范数略大于0.2，满足实际任务的精度要求。

同时，可以看出，当测量失效发生时，尽管采用了具有鲁棒功能的DVQ-REKF，相比于姿态参数，位置参数的参数估计量仍然具有相对大的误差，这也是由于姿轨耦合效应所致。因此，通过仿真分析，本文设计的DVQ-REKF虽然能够在考虑姿轨耦合因素的前提下做到一体化的参数估计，然而并不能消除姿轨耦合所带来的影响。

5 结 论

本文针对空间中的故障卫星，利用搭载2个单目相机以及一个激光测距仪作为相对信息测量敏感器的服务航天器，设计了在测量失效情况下利用双通道测量信息进行数据融合的DVQ-REKF鲁棒参数估计算法。通过仿真验证，可以看到本文所设计的位姿质量参数一体化参数估计算法有效，且DVQ-REKF能够在测量失效的条件下对目标参数做出合理估计。尽管本文所设计的算法不能完全解决姿轨耦合问题，然而相对于传统算法而言，本文所设计DVQ-REKF仍然有着一定优势，为空间故障卫星维修，航天器测控方法提供一种新的思路。