雷诺数对柱面屋盖脉动风压非高斯特性与风压极值的影响★
2018-11-13王晓梦朱召泉
邱 冶 王晓梦 朱召泉
(河海大学土木与交通学院,江苏 南京 210098)
0 引言
大跨屋盖结构因造型优美且受力合理,被广泛地运用于体育场馆、机场航站楼和会展中心等公共建筑中。由于屋盖结构周围分离流和旋涡脱落等特征湍流的影响,其表面脉动风压具有明显的非高斯特性,此时中心极限定理的前提条件不再满足,如果采用高斯模型来描述,往往会产生较大偏差[1]。叶继红等[2]研究了五种典型大跨屋盖表面局部风压的高斯和非高斯特性,非高斯分区往往集中在屋盖迎风前缘、尾流区及角部区域,并建议适当提高相应的峰值因子取值。Liu等[3]研究了大跨鞍形屋盖表面的脉动风荷载特性,受到分离流和锥形涡的影响,屋盖高角部位的风压具有明显的非高斯特性。已有研究表明[4],大跨曲面屋盖的风荷载特性具有明显的雷诺数效应,但研究大多针对平均和脉动风荷载,鲜有研究关注非高斯特性和极值风压的雷诺数效应。
本文基于矢跨比1/3柱面屋盖的风洞测压试验,分析了不同雷诺数下屋面脉动风压的非高斯特性,对高斯与非高斯进行分区,同时利用风压极值估计的改进独立风暴法,获得屋盖表面极值风压分布,并探讨了雷诺数的影响。
1 风洞试验
本次试验在哈尔滨工业大学封闭回流式风洞中进行。柱面屋盖模型采用有机玻璃制成,矢跨比R/D=1/3,宽跨比B/D=1。采用两组不同跨度的测压模型,分别为0.2 m和0.6 m,简称为小模型和大模型。试验风速U在5 m/s~24 m/s之间变化,选取模型跨度D为特征长度,依据雷诺数定义Re=6.9×104UD,得到试验雷诺数变化范围为6.90×104~8.28×105。测压信号采样频率为625 Hz,单个样本时长20 s,每组风速均采集5个样本数据。
2 试验结果分析
2.1 脉动风压的非高斯特性
对于非高斯信号,可使用三阶和四阶统计矩进行表征,称为偏度(skewness)和峰态(kurtosis),分别描述风压信号概率密度函数曲线的偏离度和凸起程度,表达式如下:
(1)
(2)
其中,Cpimean和Cpirms分别为风压系数Cpi(t)的平均值和方差。
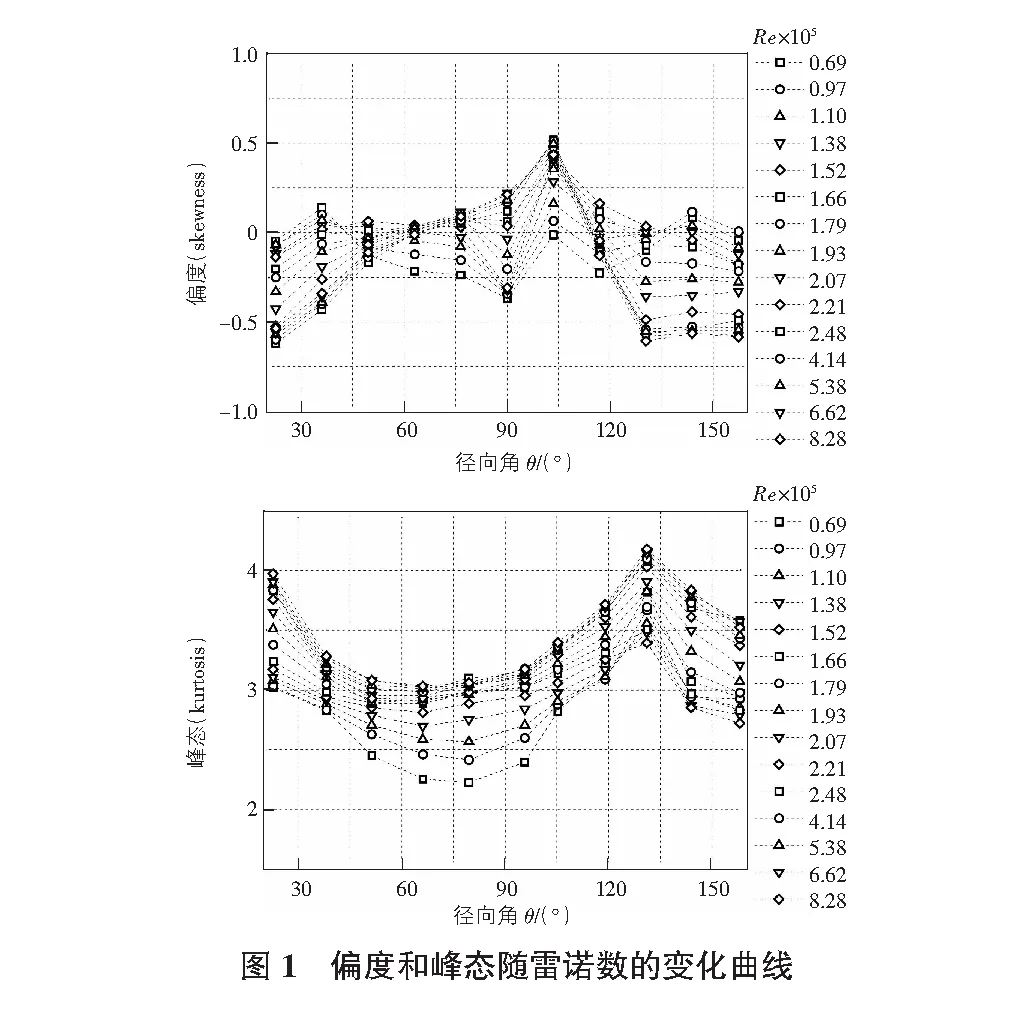
笔者在文献[5]中对矢跨比1/3柱面屋盖的风力系数—Re曲线进行了分析,已确定雷诺数转捩区(Re=6.90×104~2.48×105)和超临界区范围(Re>2.48×105)。模型中心线条带处的偏度和峰态分布随Re的变化情况如图1所示。在转捩区间内,偏度和峰态明显地受雷诺数变化的影响,且大部分测点具有较低的偏度(|Cpisk|<0.5)和峰态(Cpiku<3.5),说明测点信号大多近似为高斯分布。但当Re>2.48×105时,偏度和峰态分布形式基本与Re无关,较大偏度(|Cpisk|>0.5)和高峰态(Cpiku>3.5)分别位于屋盖迎风面(θ<38°)和尾流局部区域(θ>103°)。

为探讨脉动风压非高斯特性产生的原因,图2给出屋面典型测点的风压时程曲线及概率密度分布曲线,限于篇幅,仅给出超临界雷诺数情况(Re=8.28×105)。从图2可知,在迎风前缘局部区域内(测点1),受到柱状涡的影响,风压曲线具有明显的不对称性,带有许多间歇性的脉冲信号。而处于迎风下游和顶部区域内的测点受到特征湍流的影响较小(测点2),风压曲线基本围绕平均值波动,表现为高斯分布。在屋盖尾流区域(测点3)以及两侧边缘区域(测点4)的风压信号则呈现显著的非高斯特性。Qiu等[4]对柱面屋盖绕流的研究可知,在尾流区域存在大尺度脱落旋涡结构,同时两侧边缘区域的风压脉冲主要与屋盖侧面的分离剪切流作用有关,故产生非高斯特性的原因可归结为特征湍流的影响。
由于实际工程结构常处于超临界或高超临界范围,因此本文仅根据超临界Re试验结果给出相应测点的高斯与非高斯区的所属范围。统计结果表明,在屋盖迎风前缘、尾流区以及两侧边缘区域的测点存在大偏度(|Cpisk|>0.5)和高峰态(Cpiku>3.5),模型中部区域大部分测点都属于小偏度和低峰态情况。鉴于此,本文将满足|Cpisk|>0.5且Cpiku>3.5的测点划分为非高斯区,其余属于高斯区,如图3所示。


2.2 雷诺数对风压极值的影响
探讨不同雷诺数下柱面屋盖表面风压极值的变化规律,对围护结构的抗风设计具有一定指导作用。本文采用针对小容量样本的极值概率分析方法(改进独立风暴法),来确定具有确定保证率的非高斯风压极值,具体计算过程可参考文献[6]。
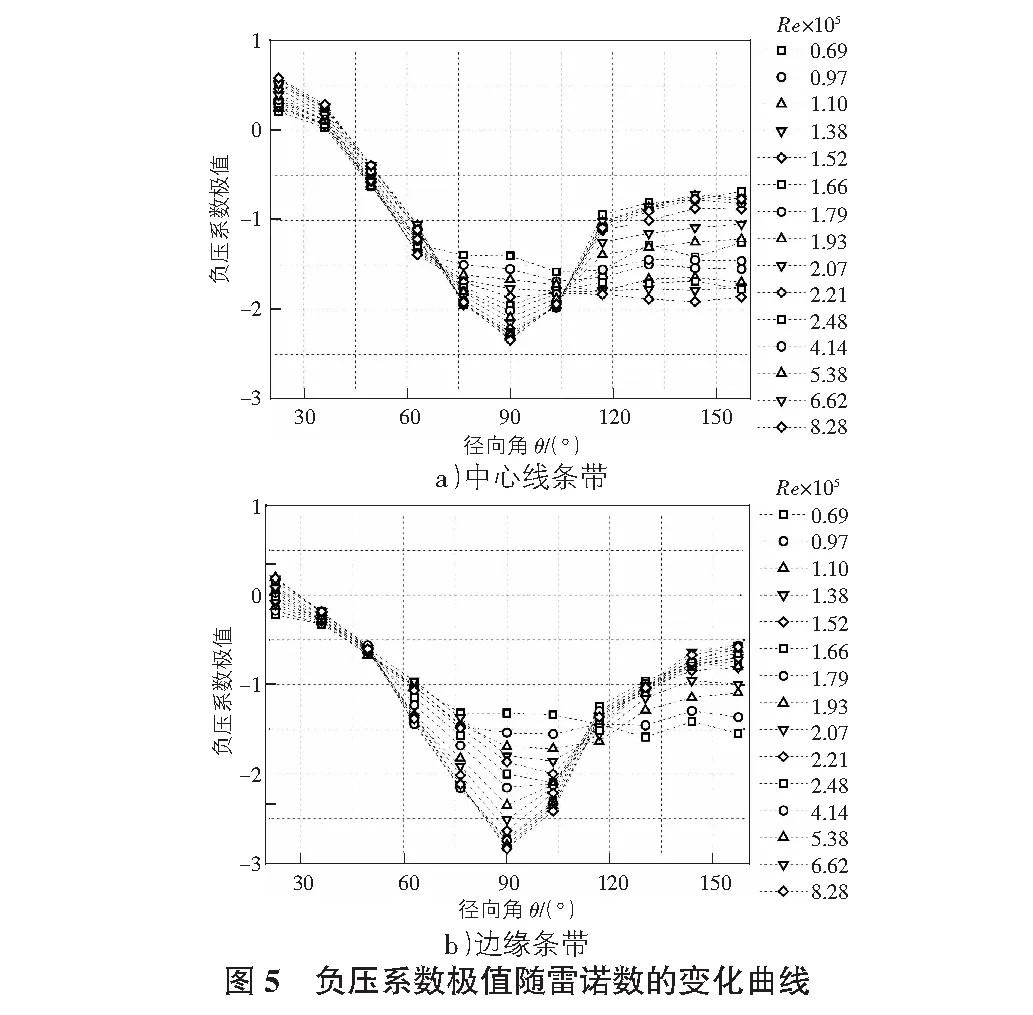
图4给出了不同雷诺数下具有95%保证率的负压系数极值分布。在转捩区间(Re=6.90×104~2.48×105)内,负压系数极值分布明显地受雷诺数变化的影响,主要与分离流发生由层流向湍流状态的过渡有关。随着Re由6.90×104增大至2.48×105,屋盖顶部区域的负压极值逐渐增大,同时在两侧接近顶部区域,由于屋盖侧面分离剪切流对风压脉动的影响增强,使得负压极值随着Re增加迅速增大。但当Re>2.48×105时,负压系数极值分布基本不再依赖于雷诺数,最不利负压极值出现在屋盖边缘局部区域。

3 结语
1)通过对风压信号第三、四阶统计矩进行归纳分析,在雷诺数转捩范围内(Re=6.90×104~2.48×105),屋面脉动风压主要呈现高斯特性,当Re>2.48×105时,屋盖迎风前缘、尾流区及顶部边缘附近表现出明显的非高斯特性,并在此基础上对高斯和非高斯区进行划分;2)雷诺数对柱面屋盖负压系数极值分布的影响显著。在雷诺数转捩范围内,屋盖顶部及边缘区域的负压极值随着雷诺数的增加而增大,但在超临界范围(Re>2.48×105)内,负压极值分布基本与雷诺数无关,且幅值最大的负压极值出现在屋盖顶部边缘区域。
