考虑失效特征的废旧零部件再制造成本预测模型研究
2018-11-13张旭刚敖秀奕江志刚
张旭刚 敖秀奕 张 华 江志刚
1.武汉科技大学冶金装备及控制教育部重点实验室,武汉,4300812.武汉科技大学机械传动与制造工程湖北省重点实验室,武汉,430081
0 引言
我国制造业飞速发展,大量机电产品目前正处在报废的高峰期,为了节约资源、减少环境污染,对退役的机电产品进行回收再利用非常有必要。对于废旧机电产品中已失效但还有利用价值的零部件,可对其进行再制造修复后重新利用。再制造企业的主要目的是为了盈利,如果废旧零部件再制造的成本高于重新再利用后产生的收益或者高于同类原件新品的制造费用,那么就没有必要对其进行再制造,因此,在进行再制造之前,对废旧零部件再制造成本进行准确预测尤为关键。由于废旧零部件失效形式不同,失效的程度也各有差异,而失效特征又是影响再制造成本的关键因素,因此从失效特征的角度对再制造成本进行分析预测非常重要。
关于再制造成本预测问题,国内外学者进行了广泛的研究。文献[1]根据采购、工艺、材料恢复和营销四个方面,计算出了再制造的成本效益;文献[2]在某些假设的前提下通过对汽车引擎回收、拆卸、清洁、库存管理等方面的分析对再制造成本进行了估算;文献[3]采用三种策略找到了回收件回收质量与再制造总成本之间的规律;文献[4]基于实例推理的方法建立了液压缸再制造成本估算模型;文献[5]通过对汽车零部件再制造的例子,提出了一个综合的再制造成本管理系统;文献[6]在再制造成本与再制造率的基础上建立了利润最大化模型;文献[7]结合射频识别(radio frequency identification,RFID)技术和RFID标签成本等因素,建立了废旧产品回收过程中各个供应者的集中和分散供应链模型,有助于节约再制造回收成本。
以上研究从成本、环境、资源、技术、工艺等方面对再制造成本展开研究,但未考虑失效特征对废旧零部件再制造成本的影响。文献[8]虽然建立了零部件失效类型与再制造成本的二元线性回归模型,但其所用的函数方法却难以表达出再制造成本真实的随机波动性。最小二乘支持向量机回归(LS-SVR)模型具有运算速度快、预测精度高的特点,可有效解决该问题[9]。
基于以上分析,本文从废旧零部件失效特征的角度出发,采用LS-SVR方法对再制造成本预测展开研究,然而实际再制造过程中,废旧零部件的再制造成本需要经过一系列的加工才能得到,其过程较为复杂,获取大量已完成再制造零件的成本信息代价太大,相对来讲大量还未进行再制造的废旧零部件信息是可以轻易得到的,因此,本文将半监督思想引入LS-SVR算法,将少量已完成再制造的废旧零部件和大量未完成再制造的零部件信息作为实验样本,建立基于半监督最小二乘支持向量机回归(semi-supervised learning based on LS-SVR,SLS-SVR)的废旧零部件再制造成本预测模型。
1 基于失效特征的废旧零部件再制造成本预测模型
1.1 预测框架
机电产品在使用过程中,受其材料性能、所处环境、载荷等因素的影响,即使是同一种零件,其失效特征也各有不同,因此单个零件的具体再制造成本也有差异。在进行预测之前,必须先对各个零件的失效特征进行评估。废旧零部件再制造成本预测框架如图1所示。
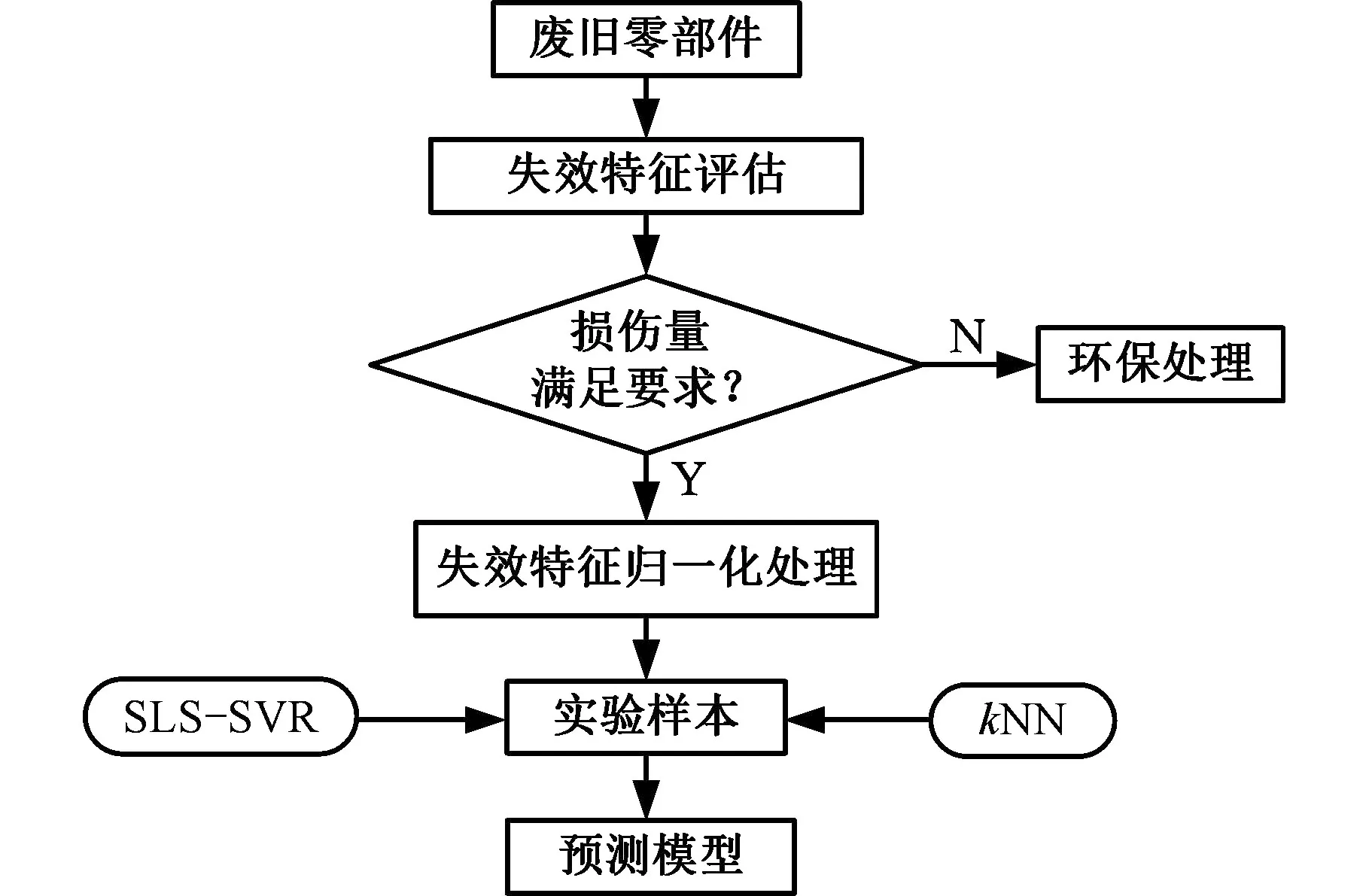
图1 废旧零部件再制造成本预测框架Fig.1 Remanufacturing cost predicting frame
对失效特征进行评估是废旧零部件成本预测的前提和基础,分析每个零部件的失效形式和失效程度并对其进行合理的量化和表达是再制造成本预测的第一步。
1.2 废旧零部件失效特征的表达和量化
废旧机电产品最常见的失效特征有磨损、断裂和变形三种。据统计,废旧机床零部件这三大失效特征造成的失效比例达75%以上。不同的零部件,其各个部位磨损量、裂纹量、变形量也各有不同,这三种失效特征一起构成了影响再制造成本的三大因素。经过对退役产品的回收、拆卸、清洗、检测等一系列工序,可得到每一个废旧零件各部位磨损量、裂纹量和变形量的具体数据,但由于这三种失效特征性质不同、单位不同,在进行计算前,必须先对数据进行归一化处理,将数据转化为量纲一的纯数值,使各类数据具有可比性。
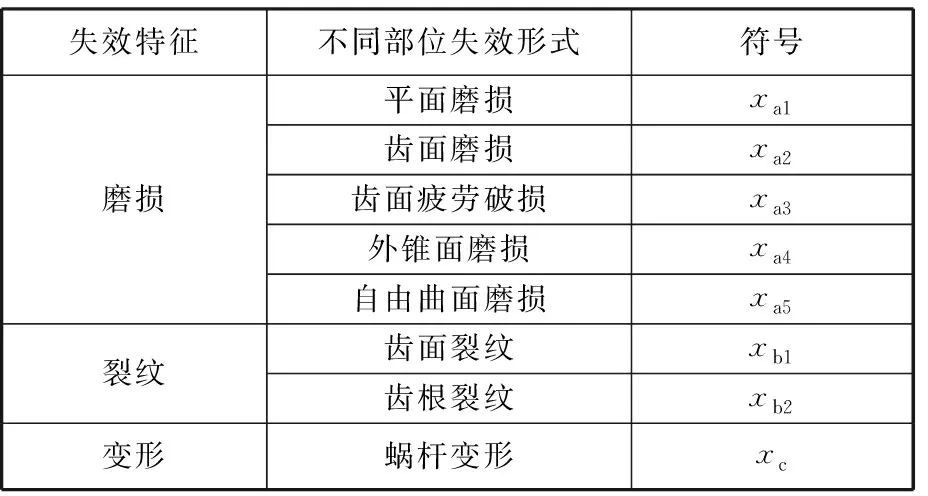
在实际再制造过程中,废旧零部件的质量状况各有差异,传统对损伤程度的描述过于模糊,难以准确预测废旧零部件的再制造成本,因此需先将损伤程度进行分区间量化,再进行归一化处理,最后利用处理后的数值对再制造成本进行预测[10]。以轴类零部件为例,表1给出了三种主要失效特征的损伤量区间及量化方法[11-12],在“min-max标准化”方法的基础上,利用模糊综合评价法对各损伤量区间分别作线性变换,将原数据映射到[0,1]区间。
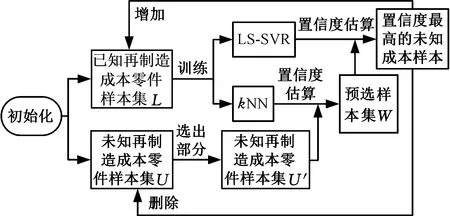
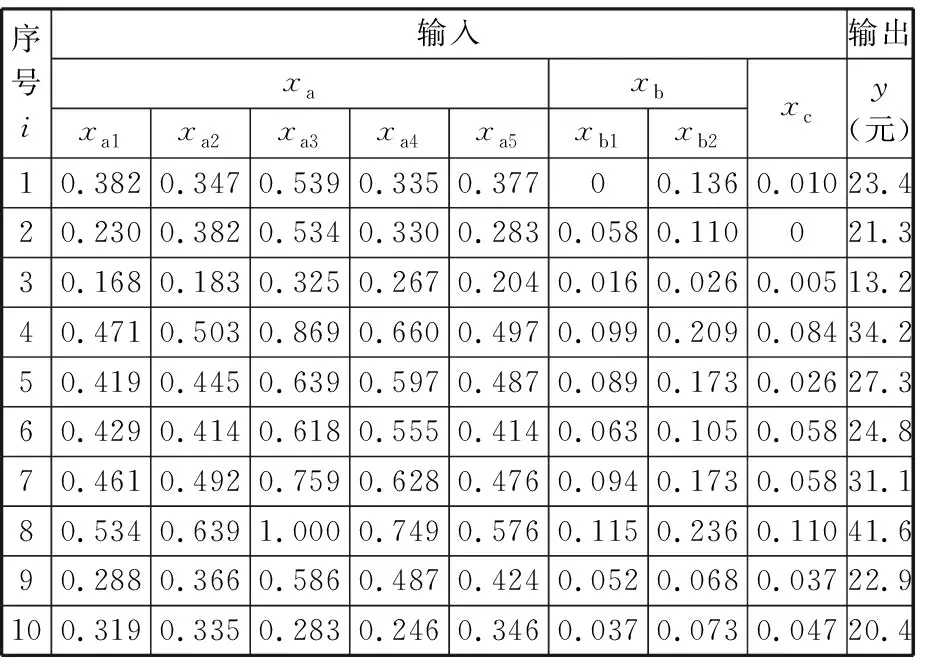
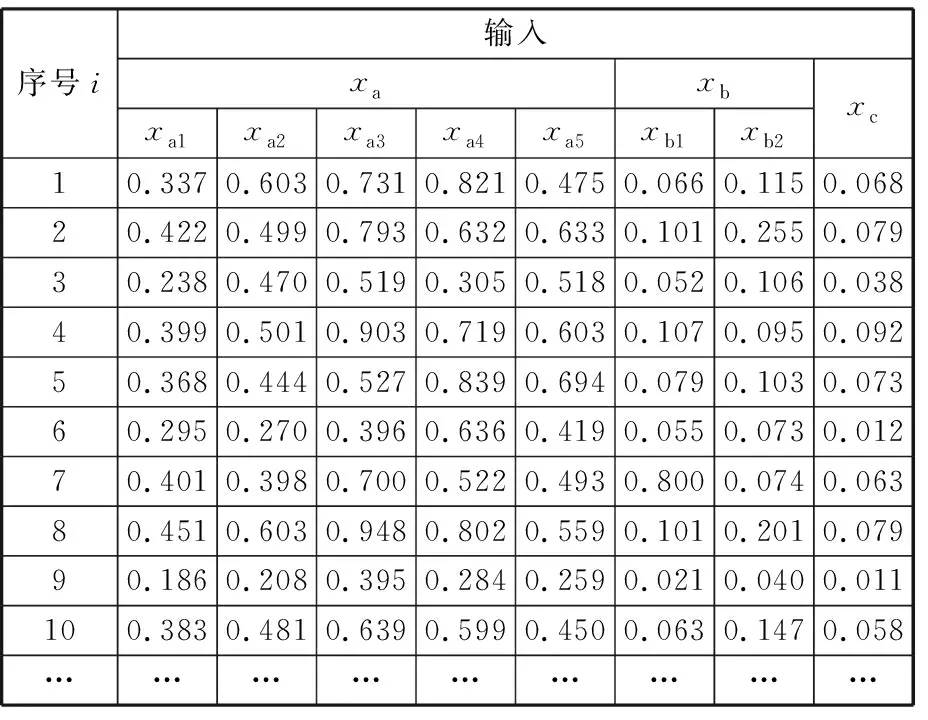
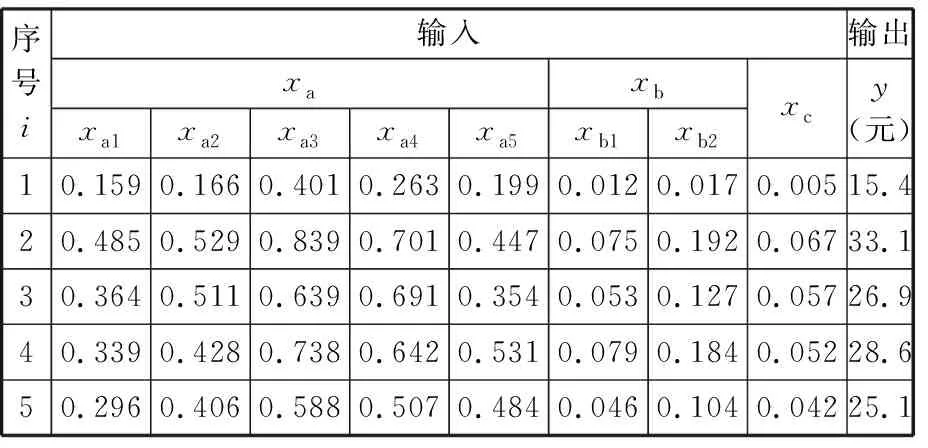
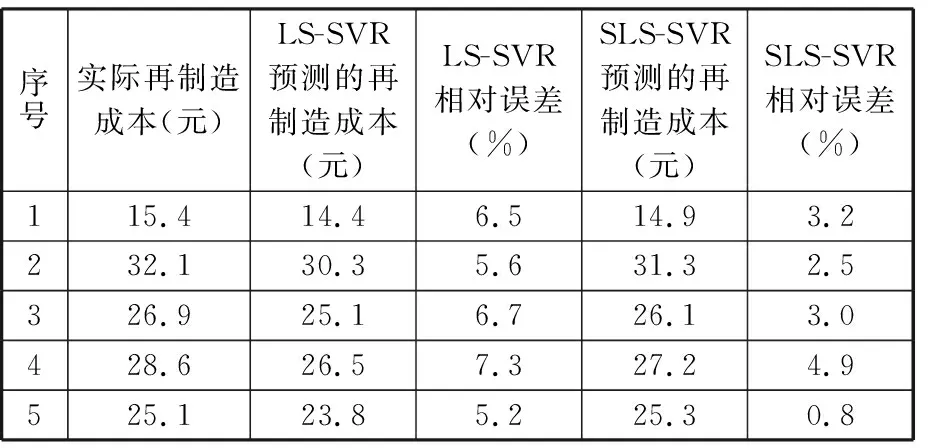
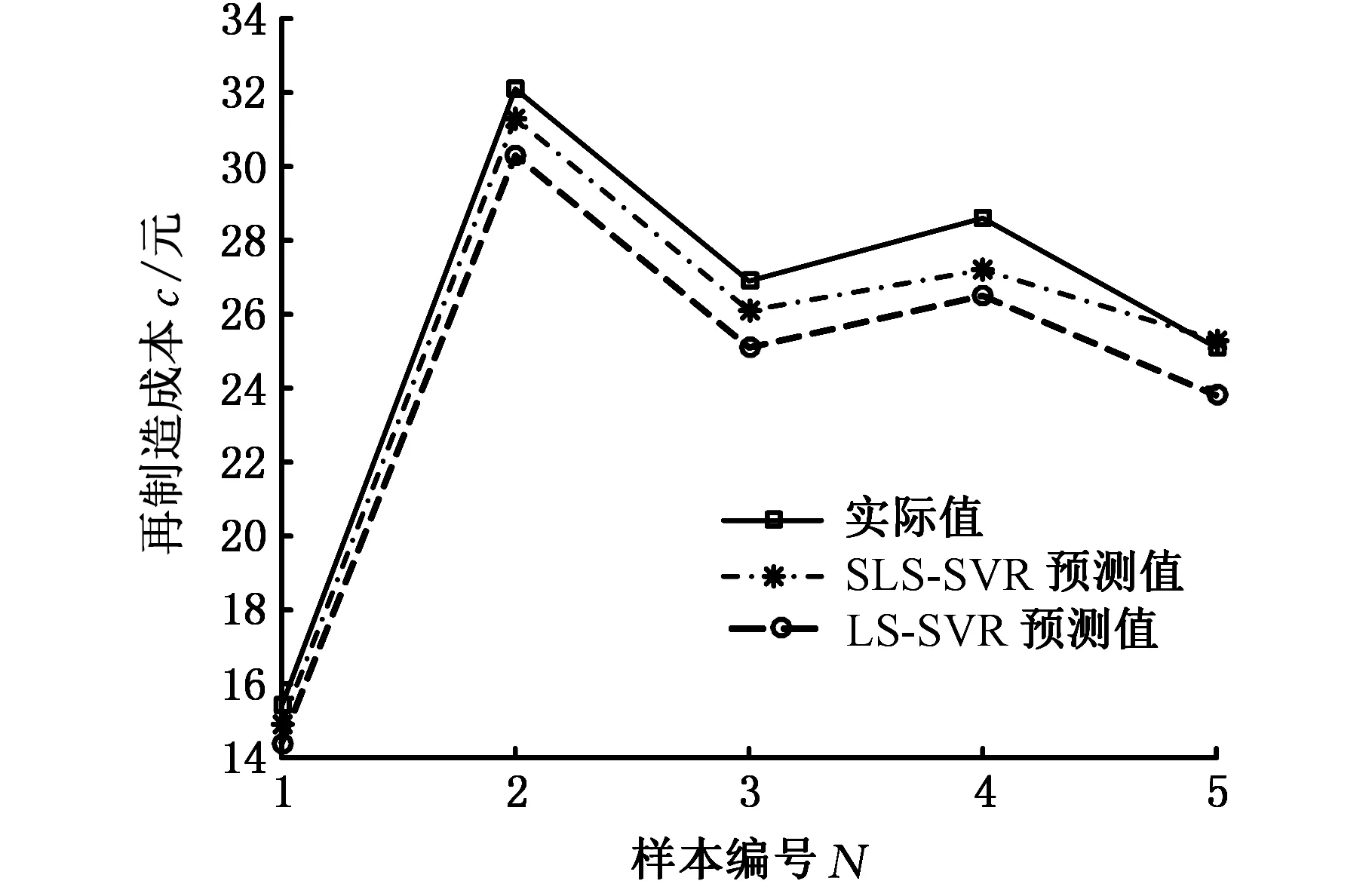
由表1可知,不同失效程度都有其对应的损伤量区间。例如某零件磨损量为v,当0 表1 轴类零件主要失效特征量化及归一化 本文基于废旧零部件的失效特征建立再制造成本预测模型,分别用xa、xb、xc分别表示废旧零部件的磨损、裂纹和变形失效特征;不同部位的失效特征具有差异性,如xa={xa1,xa2,xaj,…,xan},表示不同部位不同形式磨损量的归一化值。令第i个样本的输入为xi=(xia,xib,xic),第i个样本的输出量yi表示对应零件的实际再制造成本。给定已知再制造成本的样本集L={(x1,y1),(x2,y2),…,(xm,ym)},其中xi∈Rn,yi∈R(i=1,2,…,m),为了找到失效特征与再制造成本之间的依赖关系,在高维特征空间利用最小二乘支持向量机建立失效特征与再制造成本之间的线性回归模型[13],可表示为 f(x)=wT·φ(x)+b (1) 式中,f(x)为预测的再制造成本;φ(x)为将输入空间X(失效特征)的三个非线性属性参数(磨损、裂纹、变形)映射到高维特征空间,将原样本空间的非线性拟合问题转变为高维特征空间中线性拟合问题的函数[14];w为权值向量;b为偏置。 为了求系数wT和b,根据结构风险最小化原则,回归问题可表达为以下约束优化问题: (2) ξ=(ξ1,ξ2,…,ξm)T 式中,ξ为对应于已知再制造成本的样本集L的松弛变量;γ为正则化调节参数。 为求上述优化问题,构造Lagrange函数,将约束问题转化为无约束问题: (3) 其中,Lagrange乘数α∈R。为满足Karush-Kuhn-Tucker (KKT)条件,对式(3)中w、b、ξ、α求偏导,并令其为0,消元去掉w、ξ,可得到下列线性方程组(矩阵形式): (4) y=(y1,y2,…,ym)T Z=(φ(x1),φ(x2),…,φ(xm)) K(x,xi)=(φ(x))T·φ(xi) 式中,em为包含m个元素的全1列向量;Im为m阶单位矩阵;K为满足Mercer定理的核函数。 求得线性方程组(式(4))的解α=(α1,α2,…,αm)和b,则再制造成本预测模型为 (5) 若采用标准的有监督LS-SVR算法,需要大量已知再制造成本的零部件作为样本,由于成本获取代价较大,导致实际的样本量不能满足标准LS-SVR的要求,因此考虑将半监督思想引入LS-SVR算法中,在只有少量已知再制造成本样本的前提下,加入大量未知再制造成本的样本帮助训练。 半监督学习最普遍的一种学习方式是自训练(self-training),在self-training LS-SVR学习的过程中,首先用少量有标签样本训练出一个初始回归器,然后回归器再对无标签样本进行标记,最后将置信度最高的无标记样本加入有标签样本集中重新训练并更新回归器,以提高LS-SVR的训练精度[15]。但由于最初的有标签样本太少,初始回归器精度难免偏低,必然会得到相当数量偏差较大的标签,如此循环下去,LS-SVR的精度不增反降。基于此,引入k最近邻(k-nearest neighbor,kNN)算法帮助LS-SVR做预筛选,kNN算法先从未进行再制造零件样本集中选出置信度较高的部分样本,然后利用LS-SVR对这部分样本做置信度估算,选出置信度最高的样本加入已知再制造成本样本集中,重新训练LS-SVR,通过多次迭代,逐步提高模型精度。 图2给出了本次实验算法的完整流程,辅学习器kNN和主学习器LS-SVR对未知再制造成本的样本集U进行多层筛选,找出置信度最高的样本加入已知再制造成本的样本集L中,通过多次迭代,提高模型的预测精度。初始状态下,首先,利用样本集L分别训练LS-SVR和kNN,并从样本集U中随机选出部分样本组成样本集U′;其次,kNN对U′中的样本进行置信度评估,选出置信度最高的前三个样本组成样本集W;然后,LS-SVR对W中的样本进行置信度评估,选出具有最高置信度的样本添加到样本集L中,同时在样本集U中删除该样本。迭代多次后,LS-SVR的学习精度将得到提高[16]。 图2 废旧零部件再制造成本预测算法流程Fig.2 Flowchart of remanufacturing cost forecast 具体计算步骤如下。 (1)参数的初始设定。①确定已完成再制造零件的样本集L和未进行再制造的样本集U及迭代次数T;②确定核函数的类型及γ和σ2(σ为核函数宽度参数)的值;③kNN算法中欧氏距离测度dis和k值的设定。 (2)利用已知再制造成本集L分别训练LS-SVR和kNN得到初始回归模型G、F,从未进行再制造的零部件集U中随机选择u个样本组成样本集U′。 (3)利用F预测出U′中每一个样本的再制造成本yu,其中yu=F(xu),然后通过(xu,yu)训练kNN,得到新的回归模型F′。 (4)在已知再制造成本的样本集L中找到与xu最相近的k个样本,组成u个临近样本集Ωu,然后分别计算Ωu在F、F′上的均方差,并求其差值Δu: (6) 式(6)中,max(Δu)对应的xu即为具有最高置信度的未知再制造成本的样本,按置信度从大到小依次排序,从中挑选置信度最高的前N(N (5)利用初始回归模型G预测出W中每一个样本xj的再制造成本yj,其中yj=G(xj),然后把(xj,yj)加入到已知再制造成本的样本集L中构成新的已知样本L′,并用L′训练LS-SVR得到新的回归模型G′。 (6)计算样本集L在G′上的均方误差Ei: (7) (7)将得到的最优样本(xj,yj)加入L中, 并在未知再制造成本U中删除xj。 (8)返回步骤(2),循环训练T次,输出其回归参数α和b,得到最终的回归模型。 (9)利用测试样本判断回归模型的精度。 涡轮蜗杆是机床上重要的传动组件,也是容易失效的组件之一。本文以废旧普通圆柱蜗杆为研究对象,经过对废旧蜗杆的分析测量,其主要失效形式为磨损、裂纹和变形,具体失效特征见表2。 表2 废旧涡轮蜗杆的失效特征 经归一化处理后得到了50组数据,利用这些数据进行训练和测试,其中训练样本包含10组已知再制造成本的零部件和35组未知再制造成本的零件,测试样本为5组已知再制造成本,训练与测试样本数据见表3~表5。 为了说明SLS-SVR的优越性,采用测试样本的均方误差(MSE)衡量其回归估计性能: 表3 训练样本数据集L 表4 训练样本数据集U 表5 测试样本数据集C (8) 在MATLAB环境下,借助LS-SVMLAB工具箱,利用表3~表5的样本数据,分别对SLS-SVR和LS-SVR预测方法进行训练和测试,测试结果见表6。 由表6可知,由于SLS-SVR的预测模型将未知再制造成本的数据加入到了训练中,所以其所得的预测成本与实际成本相差更小,最大误差仅为4.9%,平均误差只有2.88%,最小均方差eMSE,min=0.706,预测结果更加理想;LS-SVR预测模型仅采用了已知再制造成本的10个样本进行训练,训练结果相对较差,最大误差为7.3%,平均误差为6.26%,最小均方差eMSE,min=2.716。图3更直观地反映了两种预测模型的预测结果与真实值的差距。 表6 预测值与相对误差 图3 再制造成本预测结果与实际结果对比图Fig.3 Comparison of remanufacturing cost between forecast results and actual results 经过训练和测试,SLS-SVR的预测模型精度更高,将废旧零部件的失效特征输入该模型,即可准确地预测出该零部件的再制造成本。 本文在分析零部件失效特征的基础上,针对再制造样本数量少的问题,结合半监督学习与最小二乘支持向量机,并采用kNN作为辅学习器建立了基于失效特征的废旧零部件再制造成本预测模型。案例分析表明,该模型不仅解决了样本量少的问题,而且具有运算速度快,预测精度高的特点,可为再制造企业快速判断废旧零部件的再制造成本和再制造性提供理论依据。 失效特征只是影响再制造成本的一个方面,影响废旧零部件再制造成本的因素还有很多,如再制造工艺、剩余寿命、资源环境影响等方面。未来将研究失效特征与再制造工艺、剩余寿命及资源环境影响相融合的再制造成本预测方法。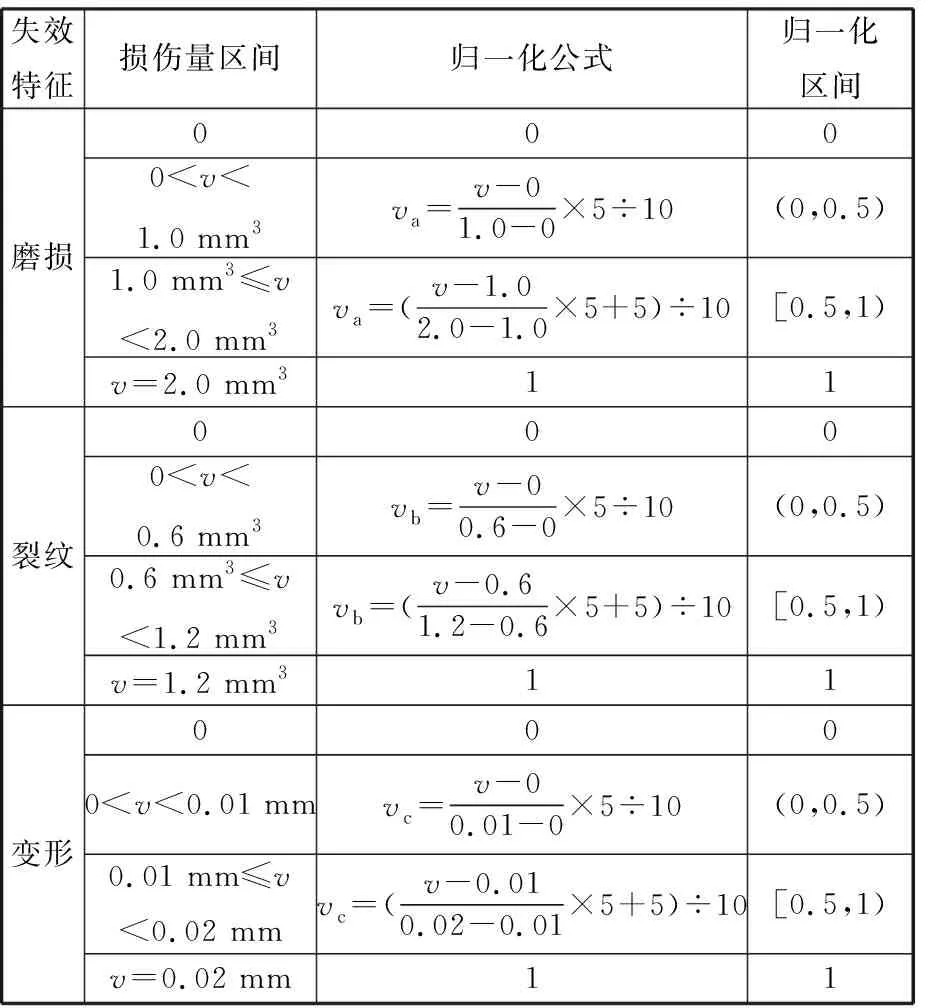
1.3 考虑失效特征的再制造成本预测模型
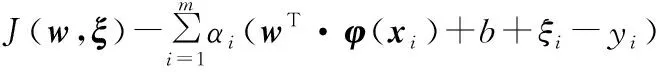
1.4 算法流程及步骤
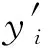
2 案例分析
2.1 参数选择
2.2 预测结果分析
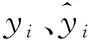
3 结语
