基于CKF的多雷达分布式再入弹道目标实时跟踪算法

李春月，廖育荣，倪淑燕，陈 帅

（航天工程大学 光电装备系，北京 101416）

0 引 言

现阶段，单雷达系统对再入弹道目标的实时跟踪精度已不能满足导弹拦截需求，人们开始研究采用多个雷达对弹道目标进行协同跟踪。多个雷达对弹道导弹的实时跟踪问题本质上即为传感器网络[1]中的最优状态估计问题。由于传统的集中式估计方法带有一个数据融合中心，多个测站的量测数据均发往融合中心进行计算与状态估计，大大增加了融合中心的通信量与计算量。近年来分布式估计方法受到越来越多的关注，该方法中每个雷达仅与其相邻雷达进行信息交互，无融合中心，可扩展性强，特殊环境下生存能力强[2-3]。

在解决分布式估计问题的众多方法中，文献[4-6]提出的基于一致性分布式卡尔曼滤波（Distributed Kalman Filter，DKF）算法引起了学者们的广泛关注。该算法利用信息滤波器（Information Kalman Filter，IKF）与平均一致性滤波器级联的方法，实现了对离散线性高斯系统中目标状态的分布式估计。引入扩展卡尔曼滤波（Extended Kalman Filter，EKF）[7]算法可以将 DKF 推广到高斯非线性系统，但由于EKF算法对非线性状态方程进行的是一阶泰勒级数展开，非线性程度不高，在强非线性系统中滤波精度较低。无迹卡尔曼滤波（Unscented Kalman Filter，UKF）[8]是基于UT变换的采样策略，采用Sigma点近似表示非线性函数的分布，有效提高了目标状态估计精度，由此基于统计线性误差传播理论的分布式UKF算法也被提出，但是该算法仍未解决UKF算法对于高维非线性系统（维数n≥4）滤波不稳定的问题。文献[9-10]通过采用Spherical-Radial规则近似非线性函数传递的后验均值和协方差的方法，依据高斯滤波框架提出容积卡尔曼滤波（Cubature Kalman Filter，CKF）算法。相比于EKF与UKF算法，CKF算法有严格的数学推导过程，在没有显著增加计算量的前提下，有效提升了算法的估计精度与计算稳定性，在各个领域得到广泛应用[11-12]，因此CKF算法更加适合作为分布式非线性滤波的基础算法。

本文提出一种基于CKF的多雷达分布式弹道目标跟踪算法，通过将CKF的信息滤波形式嵌入DKF滤波框架，得到分布式容积信息滤波器。该算法无融合中心，信息交互仅存在于具有通信链路的相邻雷达之间，每个雷达单独执行滤波计算，获得与集中式方法相近的跟踪精度，仿真结果验证了算法的有效性。

1 再入弹道目标跟踪数学模型

1.1 再入弹道动力学模型

考虑再入弹道目标的一般运动状态，对再入弹道目标进行受力分析，其主要受到的空气动力表现为大气阻力，大气阻力加速度方向与再入速度方向相反。定义以测量雷达为原点的北天东（North-Up-East）坐标系O-xyz，Ox指向正北方向，Oy垂直于地球表面指向正上方，Oz指向正东方向。由于再入弹道导弹速度快，再入时间短，忽略地球自转角速度的影响。对再入目标建模如图1所示，假设地球为标准球体，Oe为地球质心，ag和af分别为引力加速度和大气阻力加速度，弹道目标的位置、速度分量和弹道系数构成7维状态向量，给出再入弹道目标的系统状态方程：

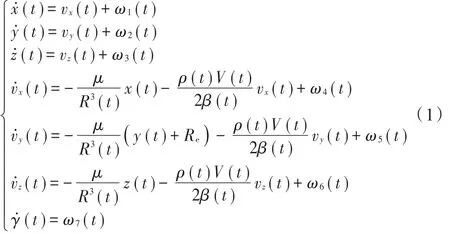
式中：CD为气动阻力系数；m为弹道目标质量；A为弹道目标有效截面积。为了保证弹道系数的非负性，防止滤波器发散，采用式（2）的指数模型，γ(t)的变化率可以用零均值高斯白噪声表示，即：

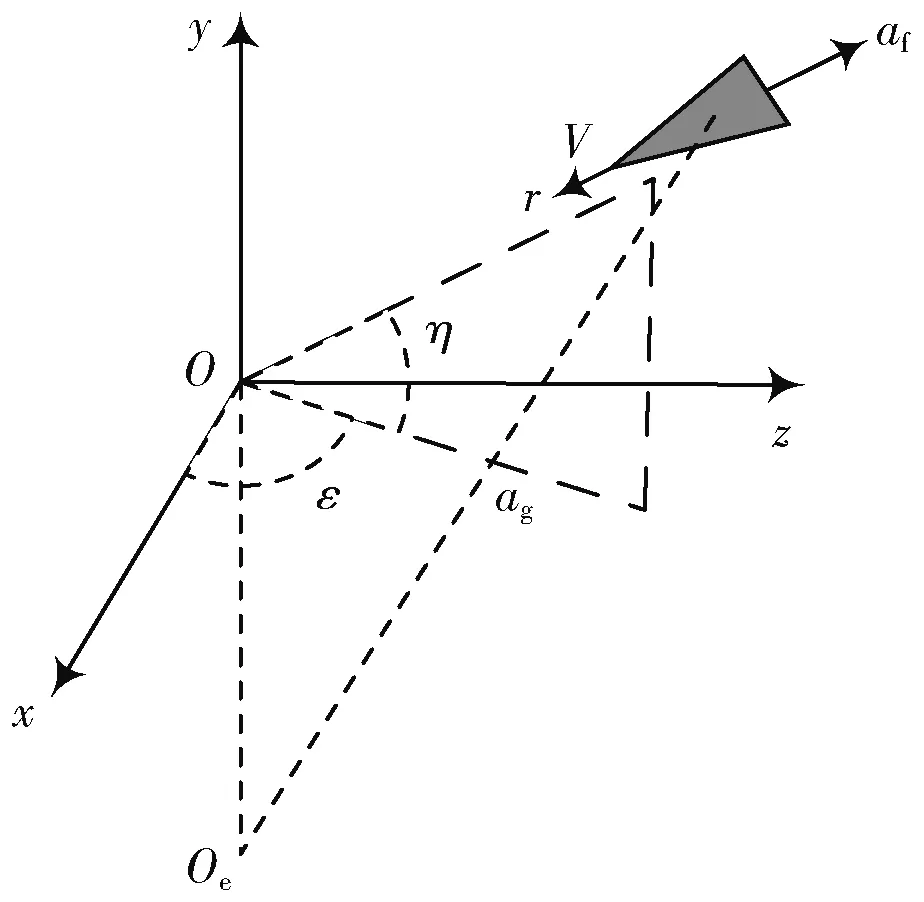
图1 雷达观测再入弹道目标示意图Fig.1 Schematic diagram of reentry ballistic target observed by radar

由此可以得到再入弹道目标的7维状态方程、状态量。为了保证滤波器的精度，采用四阶龙格-库塔方法对状态方程进行离散，离散的基本模型如下：

离散后的结果及相应参数为：

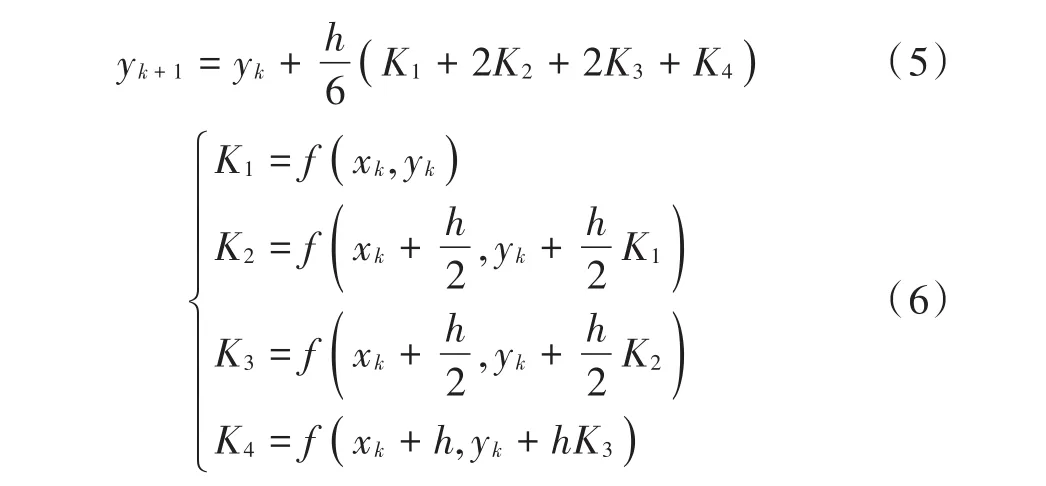
最终得到离散非线性系统状态方程为：

1.2 多雷达量测模型

多雷达量测系统中，假设共有5个雷达测站，分别采用集中式模式与分布式模式。雷达测站间的通信拓扑结构如图2所示。集中式模式中，雷达测站仅担任量测任务，量测数据统一发往数据融合中心进行跟踪计算；分布式模式中，各雷达测站间同时担任量测与目标跟踪任务，通信链路仅存在于相邻雷达测站间。

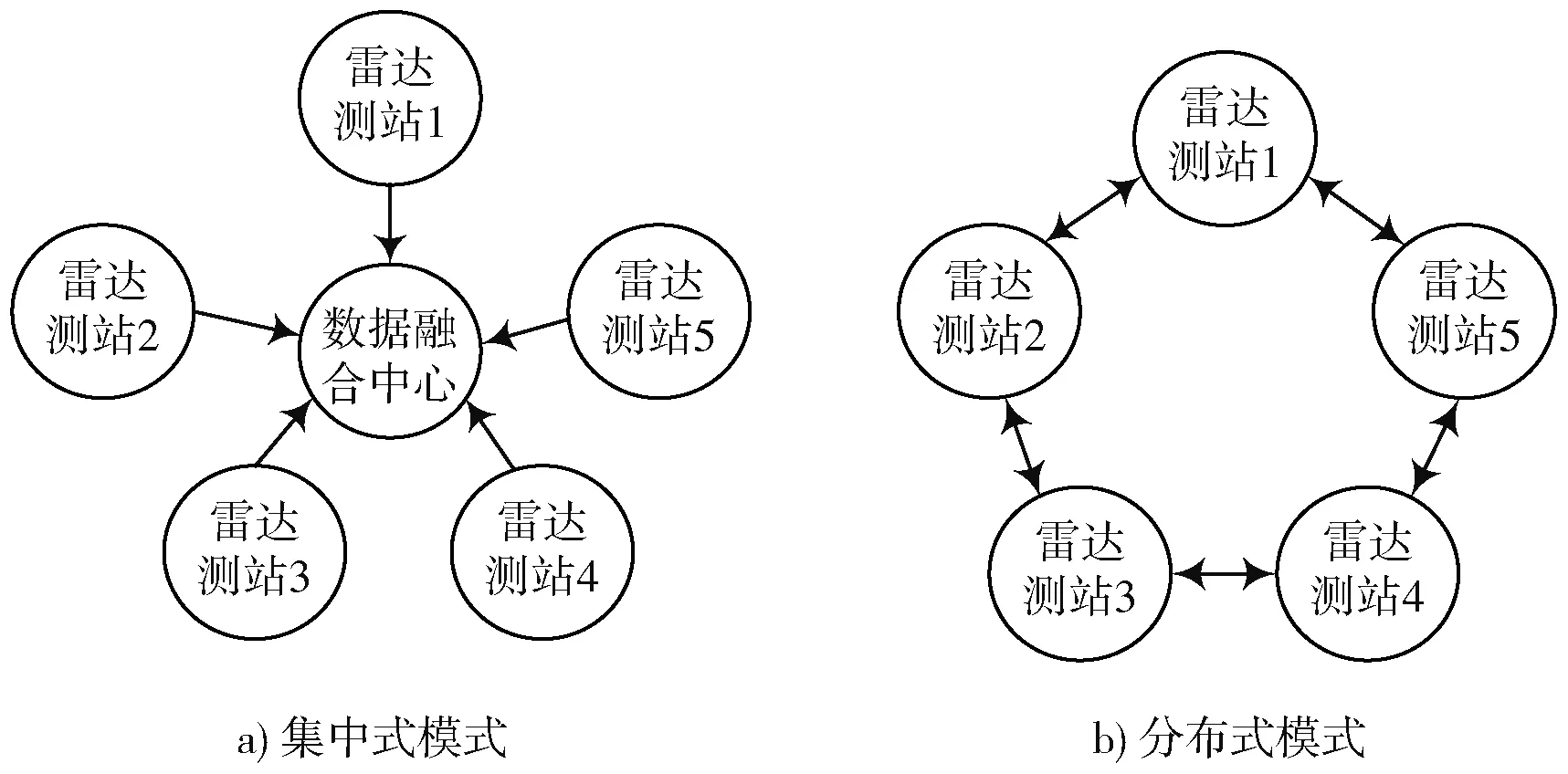
图2 雷达间的通信拓扑结构示意图Fig.2 Schematic diagram of communication topology structure among radars

在北天东坐标系下建立雷达观测再入弹道目标的量测模型。如图1所示，雷达对弹道目标的距离为r，俯仰角为η，方位角为ε，有z=[r,ε,η]Τ。由观测值相对弹道目标位置的几何关系建立非线性量测方程：

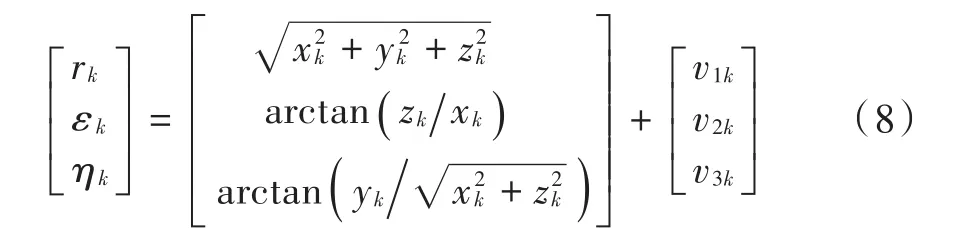
2 多雷达分布式弹道目标跟踪算法

多雷达分布式弹道目标跟踪算法本质为传感器网络中的目标估计问题，需要通过图论实现各雷达测站间通信拓扑的数学语言描述。结合平均一致性算法，通过相邻雷达间进行双向信息交互，使滤波过程中的某个中间量实现全局的一致，最终完成弹道目标的分布式估计。该模式不存在数据融合中心，滤波跟踪算法在各雷达测站下分别进行。首先考虑常规离散非线性系统：

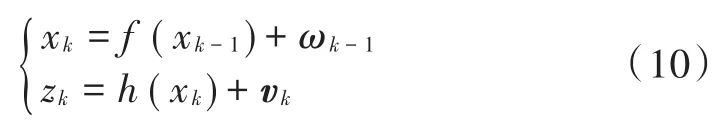
式中：噪声ωk，vk相互独立，统计特性分别满足ωk～N(ωk;0,Qk)，vk～N(vk;0,Rk)。

2.1 基础理论

用无向图G=(V,E)对由n个雷达测站的通信拓扑结构进行数学建模，其中，V=[1,2,…,n]表示雷达测站集合，无向图G中的通信链路由表示，此时雷达s与雷达j连通。雷达s的连通雷达集合记为所以有Ns⊂V。无向图G中，集合Ns中元素的个数记为雷达s的度，有无向图G中，如果任意两雷达之间存在一条通信路径（可以为多跳），则称该无向图是连通的。

传感器网络中的一致性策略规定了每个节点在仅与邻居节点通信条件下更新自身状态的过程，其中最直接的方法即为将节点自身的状态更新为自身和邻居节点状态的加权线性组合，记为[14]：

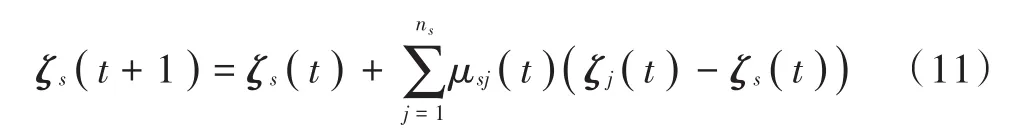
式中：ζs(t)为节点状态信息矩阵；μsj(t)为Metropolis加权系数[15]，可由式（12）计算得到。

由式（12）可以看出，加权系数仅和节点自身与其邻居节点的度有关，无需全局信息，基于此可进行分布式滤波算法设计。

引理 1[16]：假设ζs(0)为节点s的初始状态，若对于所有节点，无向图G都连通，则根据式（11）所示的一致性算法，所有节点的状态将收敛于初始值的线性组和，即：

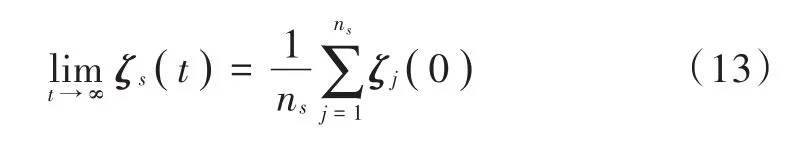
2.2 扩展信息滤波器

由于卡尔曼滤波的信息滤波形式可以用信息状态向量与信息矩阵分别累加的形式实现多元信息融合，尤其适合作为分布式算法中的信息融合方法，所以这里首先介绍非线性卡尔曼滤波的信息滤波递推公式。扩展信息滤波器（Extended Information Filter，EIF）实际上为EKF的等价信息表示，具体方法为：将EKF中的状态向量与误差协方差矩阵求逆，得到信息矩阵与信息状态向量EIF 算法的主要执行步骤为：

1）时间更新

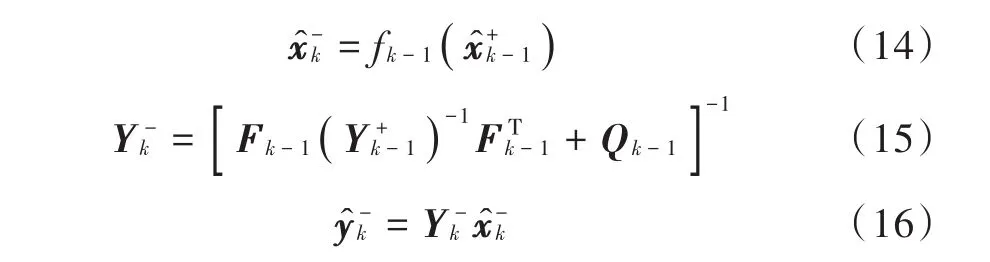
2）量测更新

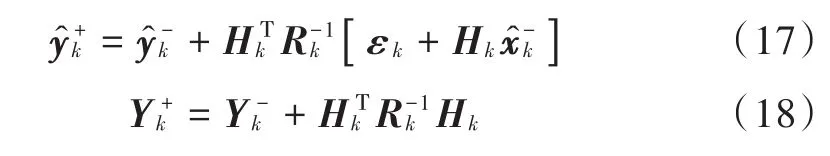
3）状态更新

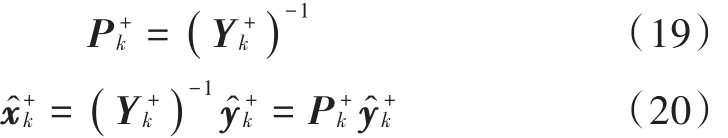
上述即为EIF算法的递推更新过程。

2.3 容积信息滤波器

这里首先介绍CKF算法。CKF算法通过球面-相径容积准则选取一组等权值的容积点来近似状态函数的后验概率分布，对于状态维数为n的非线性高斯系统，容积点的选取规则为：

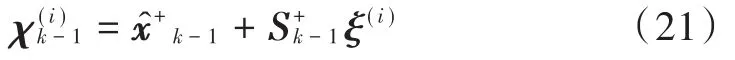
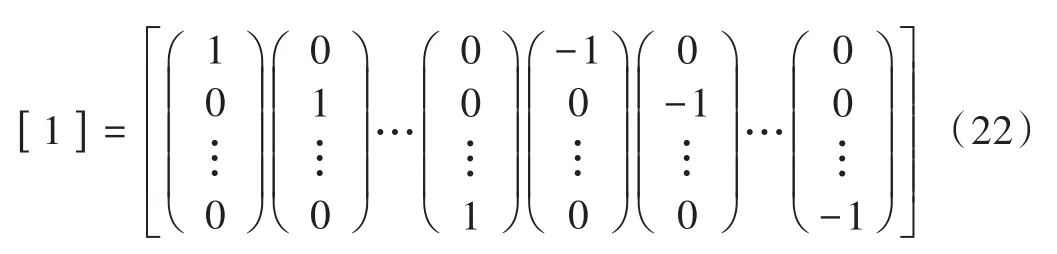
然后进行时间更新过程：

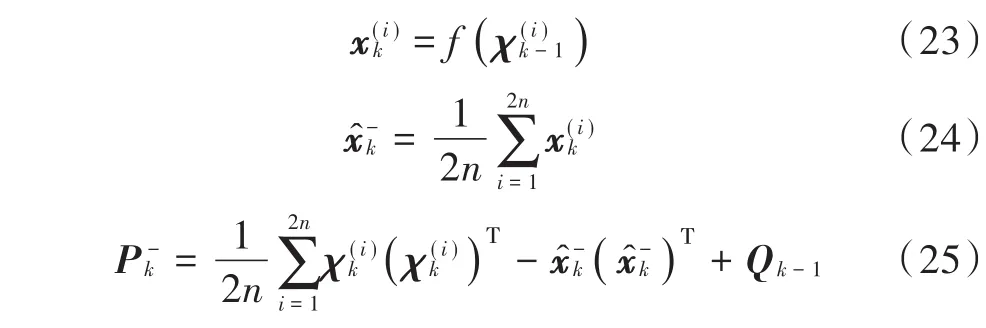
最后进行量测更新过程：

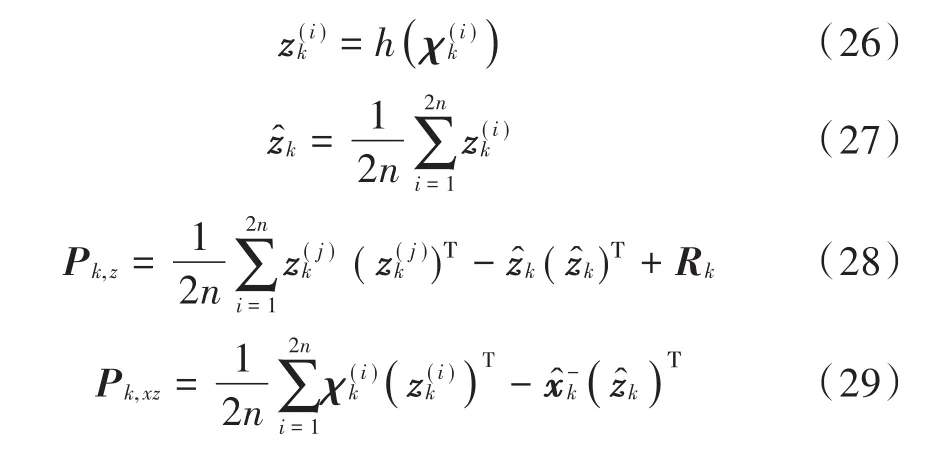
计算k时刻滤波增益：

完成状态向量与协方差矩阵的更新：

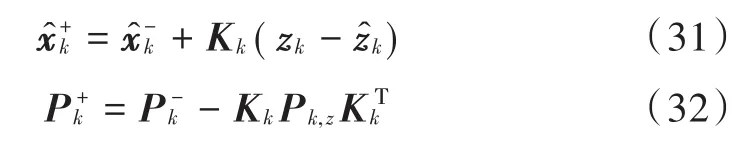
以EIF为框架进行容积信息滤波器（Cubature Information Filter，CIF）设计。首先要明确EIF中时间更新与量测更新以逆协方差矩阵为基础，并涉及线性观测矩阵，而CKF算法中状态方程与量测方程均为非线性系统，不存在线性观测矩阵，这时需要利用线性误差传播理论，利用协方差与互协方差等效表示EIF中的线性观测矩阵，即：

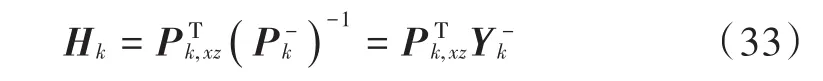
将式（33）代入式（17），式（18）得到CIF算法的量测更新：

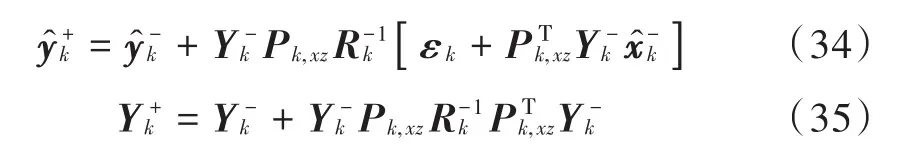
2.4 DCKF算法实现

考虑由ns个雷达测站组成的再入弹道目标实时跟踪系统，第s个测站的量测方程为：

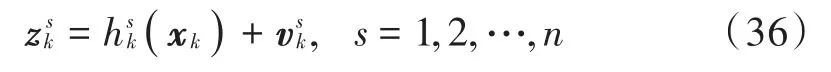
若采用有数据融合中心的集中式滤波方法，所有量测数据均由融合中心处理，则式（34），式（35）可以改写为：

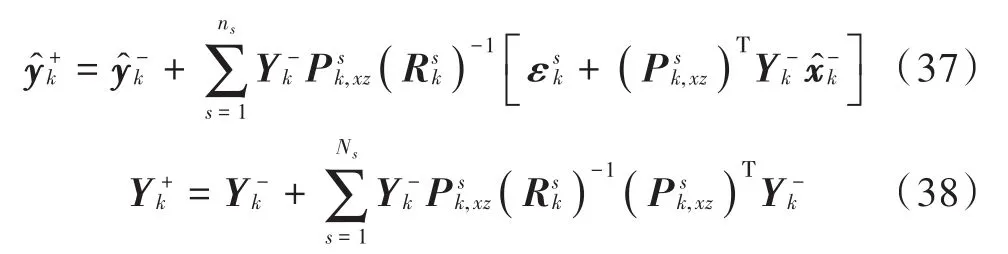
此时重新定义平均观测向量与平均逆协方差矩阵，有：

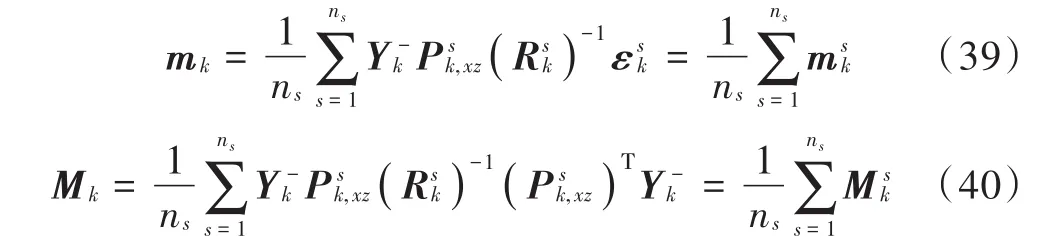
则式（37），式（38）可化简为：

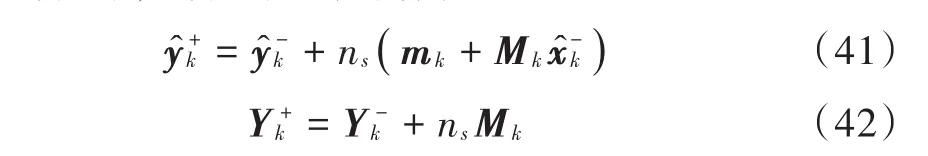
结合一致性策略与引理1观察式（41），式（42），可以发现若各个雷达测站有相同的初始信息状态，则可以通过具有通信链路的相邻雷达进行信息交互，然后结合平均一致性算法使平均观测向量与平均逆协方差矩阵达到一致，从而以分布式的方式实现多雷达集中式弹道目标跟踪算法的近似估计。进而总结出基于CKF的多雷达分布式再入弹道目标实时跟踪算法执行步骤如下（雷达测站s）：

1）初始化

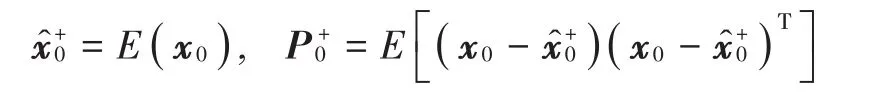
2）时间更新

式（21）～式（25）为时间更新过程，得到一步状态估计与先验误差协方差矩阵。

求时间更新的信息状态向量与信息矩阵：

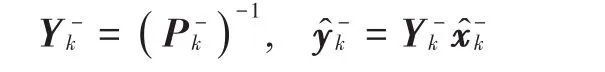
3）量测更新

设定平均观测向量与平均逆协方差矩阵初值：

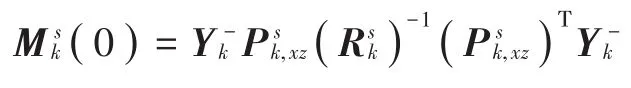
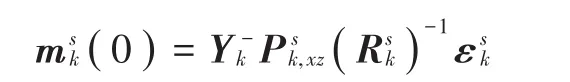
循环t=0,1,2,…,τ，τ∈N为达到一致时的迭代次数：

输出：

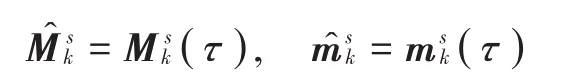
4）状态更新

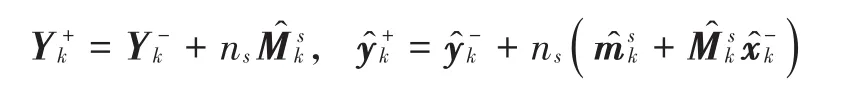
通过式（19），式（20）求得更新后的后验状态向量与误差协方差矩阵。

3 仿真分析

在Matlab R2010b环境下对多雷达分布式观测再入弹道目标系统进行建模仿真，对提出的基于CKF的多雷达分布式再入弹道目标实时跟踪算法进行验证。仿真过程中，首先基于状态模型，在雷达站坐标系下生成带有状态噪声的再入弹道目标的真实轨迹，给定再入初值为：

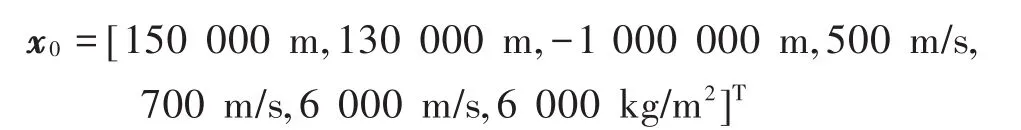
然后用四阶龙格-库塔方法对状态方程进行离散时，离散步长h=1 s。根据量测模型生成带有量测噪声的测量信息用于滤波。状态噪声协方差矩阵、量测噪声协方差矩阵分别为：

生成的再入弹道目标真实轨迹如图3所示。

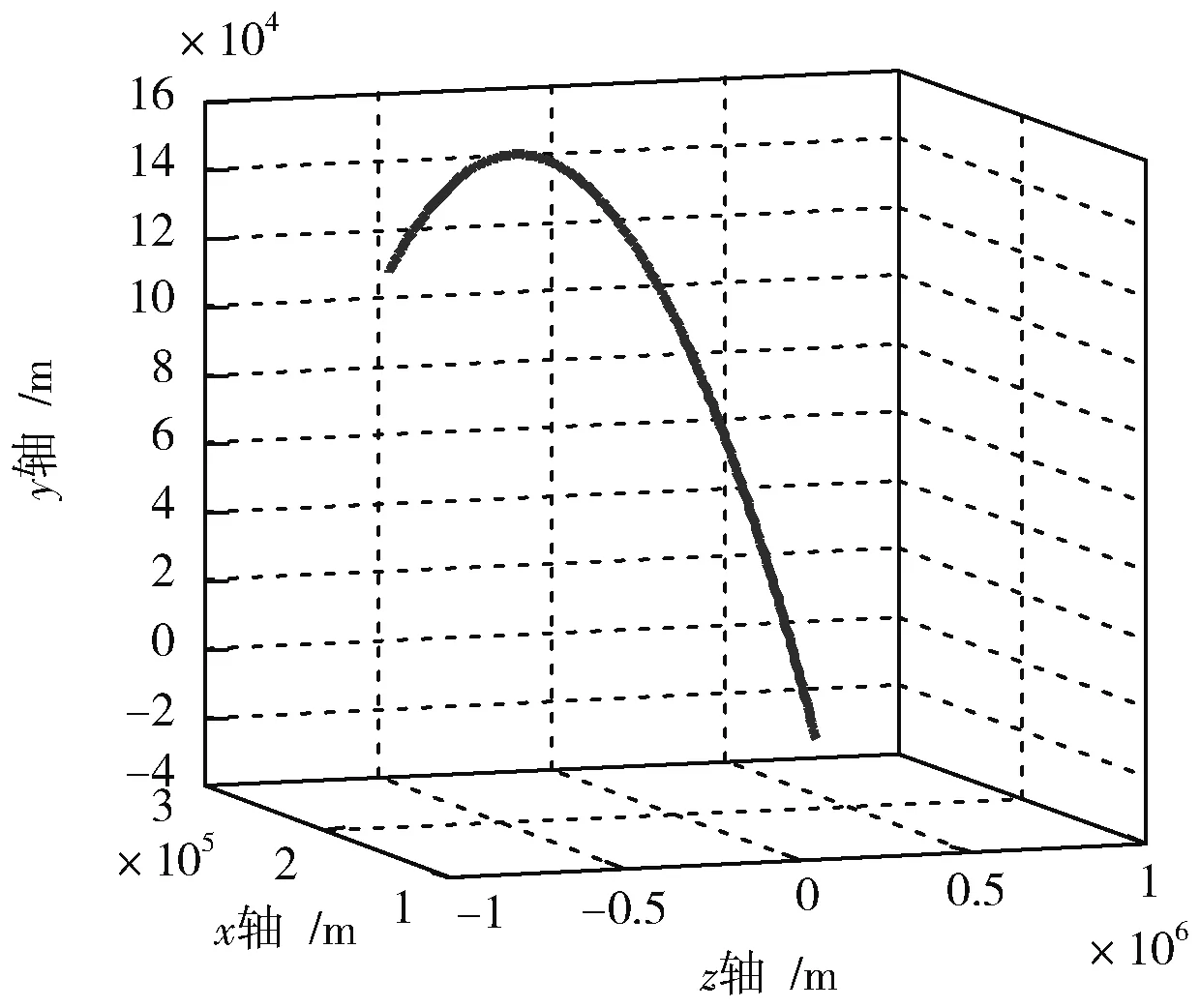
图3 再入弹道目标的运动轨迹Fig.3 Motion trail of reentry ballistic target

设定蒙特卡洛打靶次数为500次，分别以单站CKF滤波算法、基于CKF的多站集中式跟踪算法与基于CKF的多站分布式实时跟踪算法对上述弹道轨迹进行实时跟踪仿真。分布式算法的通信拓扑结构如图2b）所示，采用的是无中心的环形结构，每个测站与相邻的两个测站间具有双向通信链路；集中式CKF算法采用的是图2a）所示的通信拓扑结构，数据融合中心仅接收量测信息，不参与量测过程。

给出3种算法的滤波初始状态向量与误差协方差矩阵：

通过统计各个时刻的位置均方根误差与速度均方根误差来验证所提算法的有效性，其中位置均方根误差计算公式为：

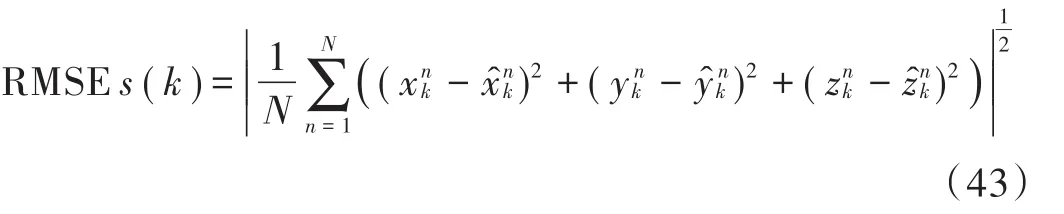
仿真结果如图4，图5所示，给定相同的估计初值与噪声矩阵情况下，其中图4为3种算法的速度均方根误差，图5为统计的3种算法的位置均方根误差。通过观察误差曲线，发现多雷达系统跟踪载入弹道目标的收敛速度明显高于单雷达系统。其中，集中式算法的实时跟踪精度最高，分布式算法相较于集中式跟踪精度有稍微下降，但是远高于单雷达测站的测量精度。

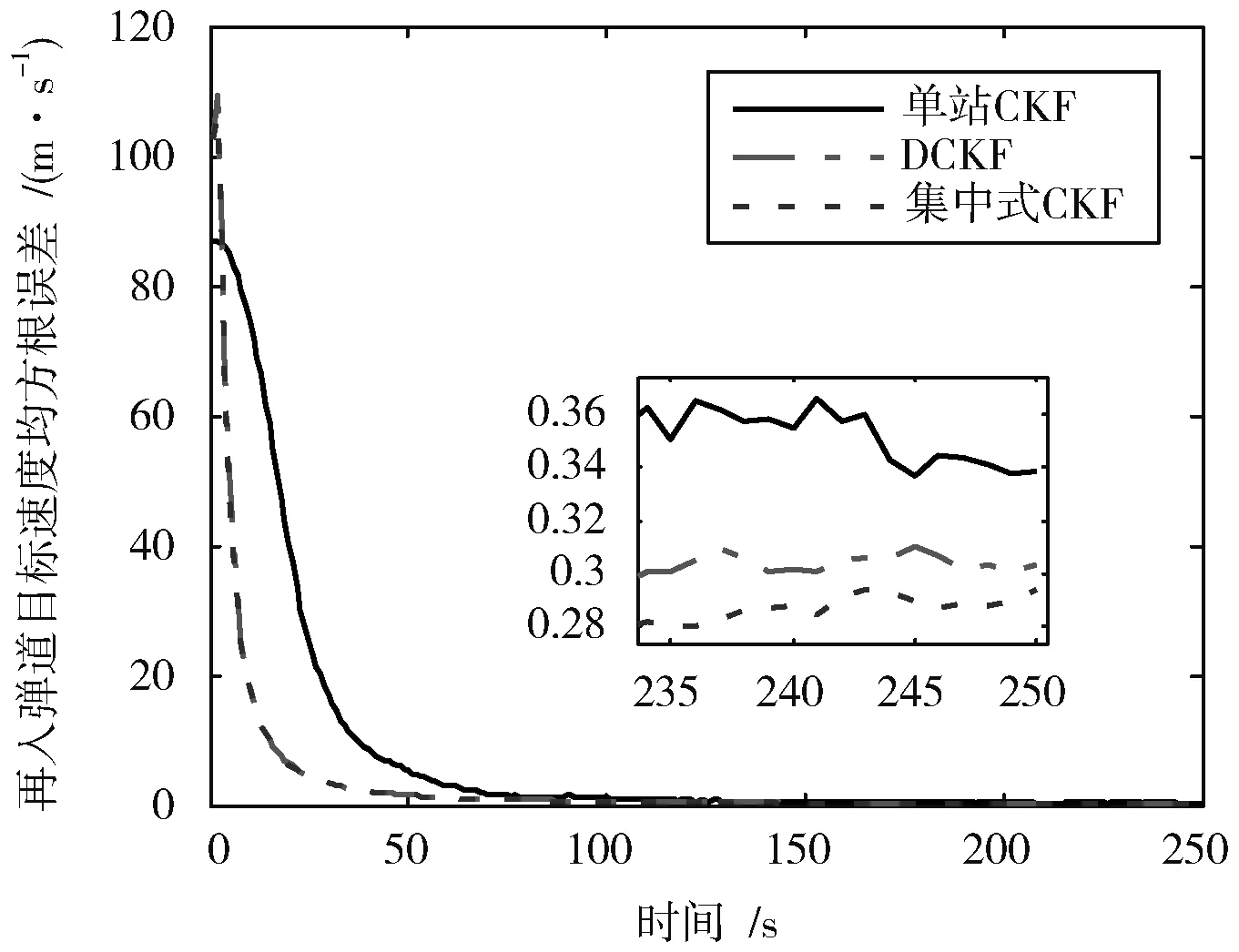
图4 弹道目标速度均方根误差Fig.4 RMSE of ballistic target velocity

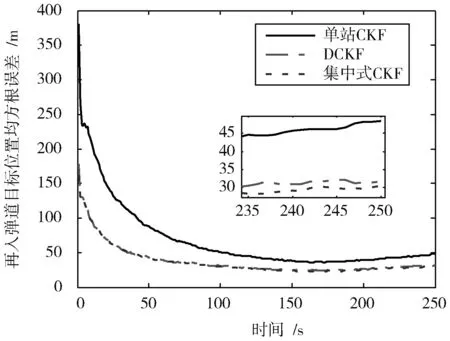
图5 弹道目标位置均方根误差Fig.5 RMSE of ballistic target position

表1统计了3种算法最后100 s仿真结果的平均值。从表1中能直观地看出，基于CKF的分布式再入弹道目标实时跟踪算法在降低通信量与计算量的前提下保持了较高的跟踪精度，相比于单站CKF算法，速度RMSE降低了0.1 m·s-1，位置RMSE降低了14 m；与多站集中式CKF算法精度相近。

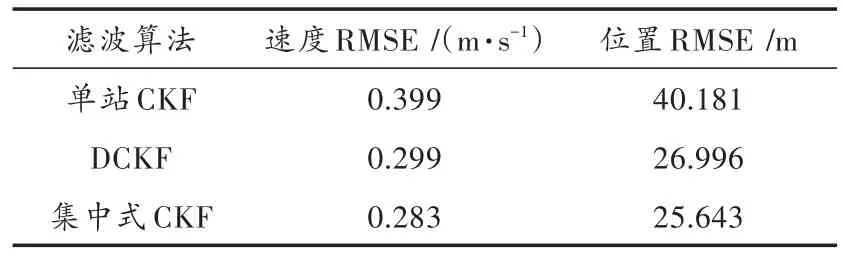
表1 150～250 s速度与位置均方根误差均值Table 1 Mean of RMSE of position and velocity with in 150～250 s

表2为相同仿真条件下，蒙特卡洛打靶次数为300次时，2种算法进行250 s再入目标跟踪时的耗时统计，侧面反映出了2种算法的计算量大小。通过对比发现，DCKF算法的计算用时较集中式CKF算法有明显减少，表明对同一目标进行相同时长跟踪时，DCKF算法具有显著降低运算量的优势。

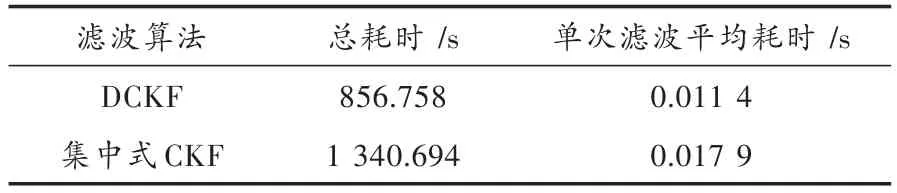
表2 跟踪250 s时2种算法计算耗时比较Table 2 Comparison of time consumption of two algorithms after reentry target tracking for 250 s

4 结 论

本文提出一种基于CKF的多雷达分布式弹道目标跟踪算法，通过统计线性误差传播的方法将CKF嵌入扩展信息滤波器得到容积信息滤波器，然后利用一致性算法将多量测值集中式滤波进行分布式等价表示，以更新状态估计与误差协方差矩阵得到DCKF算法。该算法中，信息交互仅存在于具有通信链路的相邻雷达之间，每个雷达单独执行滤波计算，获得与集中式方法相近的跟踪精度，仿真结果验证了本文算法的有效性。