一种适用于电缆通信的自适应比特分配算法
2018-11-13刘豆豆刘得军
刘豆豆,刘得军,程 星,闫 松,王 辰
(中国石油大学(北京),北京 102249)
0 引 言
随着正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)[1-2]在无线通信领域的不断发展与成熟,以及其高效率的调制模式,该技术在有线通信领域也得到广泛的应用。在石油测井方面,井下仪器与地面仪器之间的数据传输及通信、井下仪器的供电均采用电缆传输。在长距离电缆传输中,电缆带宽有限,信道具有选择衰落特性,每个子信道的数据传输能力不同[3],但是在电缆通信中,通常各个子信道采用统一固定的调制方式,这样系统的传输能力主要由深度衰落的子信道决定。井下环境多变,信道特性在一定的时间内会发生变化,为确保传输准确性,本文将自适应分配技术应用到电缆通信中,每隔一定时间对信道特性进行估计,根据各个子信道特性采用不同的调制方式,从而优化系统性能,提升传输速率[4]。
根据RA(Rate Adaptive)准则,在发送功率和系统传输性能误比特率(Bit Error Rate,BER)一定的前提下,实现信息传输速率最大化[5]。在该准则下通常多采用的自适应算法有Chow算法[6-7]和注水算法[4]。注水算法适用于非离散比特分配,而实际调制中星座点数是离散的,则考虑Chow算法,但是Chow算法由于算法限制,优化余地有限。本文在满足电缆传输要求的前提下,提出一种算法复杂度低的比特分配算法,本文统一称为比例贪婪算法。
1 比例贪婪算法模型
1.1 算法思想
比例贪婪算法流程图如图1所示。
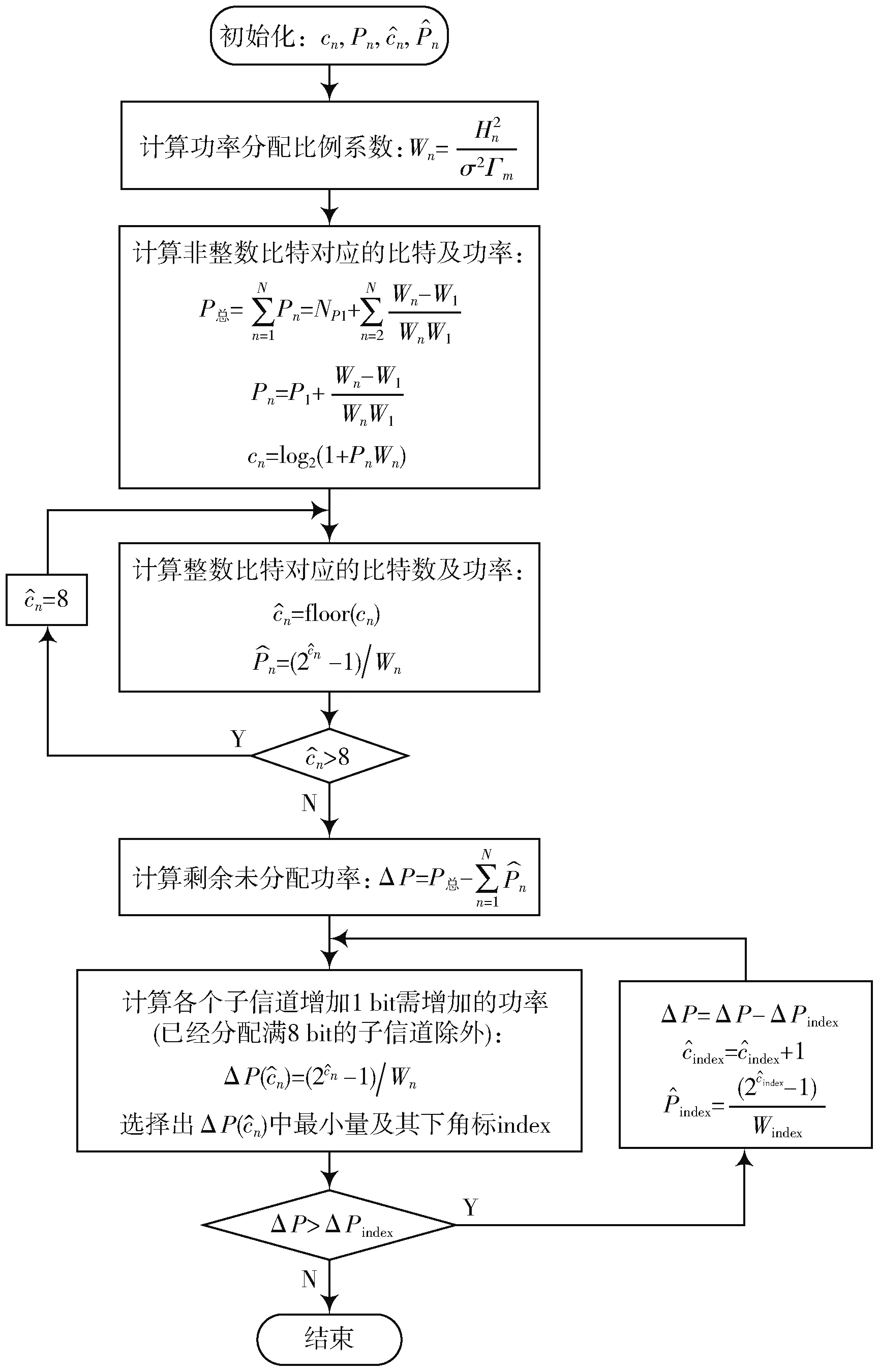
图1 比例贪婪算法流程图Fig.1 Flow chart of proportional greedy algorithm
该算法首先根据信道估计特性以及信噪比间隔确定各个子信道的功率分配,其中信噪比间隔与调制方式有关,根据各个子信道分配的功率,分别求出各子信道比特分配数目,然后将求出的比特数目向下取整,得到整数比特分配,根据得到的整数比特返回求对应的消耗功率(由于比特数目都是向下取整,故消耗的功率比最初分配的功率小),求得消耗功率总和,然后再求出剩余未分配的功率,根据贪婪算法逐比特分配剩余未分配的功率,直到剩余功率不能再分配任何一个比特[8]。
1.2 算法步骤
1)功率分配
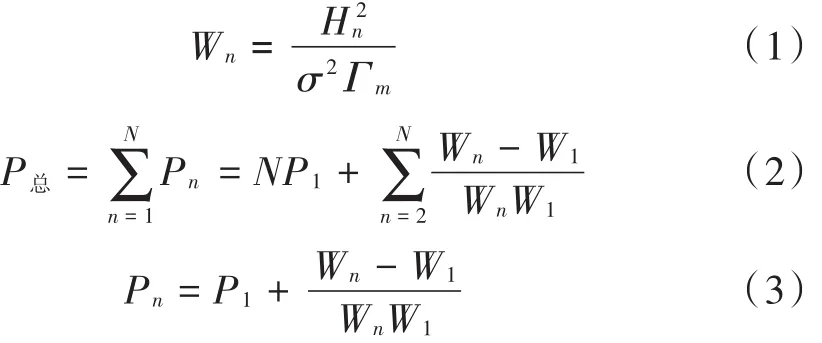

2)比特分配

3)比特取整,if≥ 8,则=8,不再变化。

4)整数比特对应功率
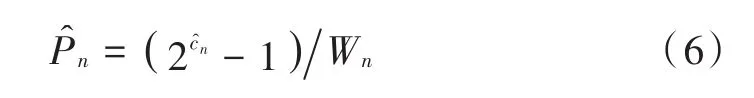
5)求剩余未分配功率

6) 根据贪婪算法分配剩余功率 ,=+1 ,if=8,则不再增加。

7)重复步骤4)~步骤6),直至剩余功率不够分配任意比特。
1.3 算法分析
由功率分配比例系数可知,功率分配不仅与信道的信噪比有关,同时也受信噪比间隔的影响。对于M-QAM调制,信噪比间隔又与子信道选择的调制方式和误码率有关[10-11],所以对于自适应比特分配系统,每个子信道信噪比间隔不一定一致。经过计算,信噪比间隔随着子信道调制方式(分配比特数)变化见表1。
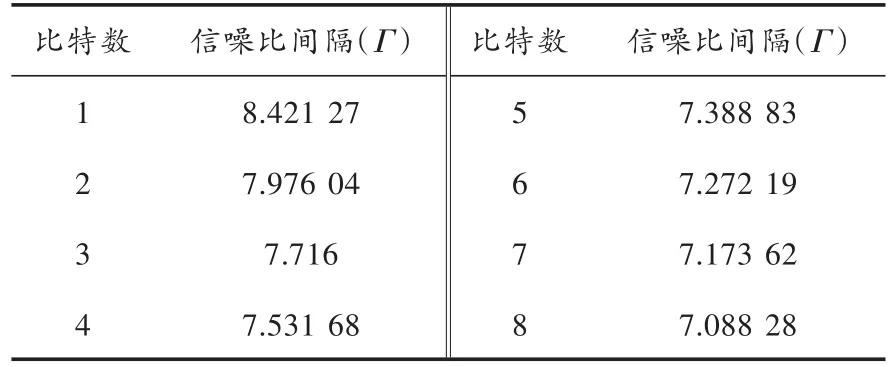
表1 比特数与信噪比间隔之间的对应关系Table 1 Correspondence between the bit number and SNR gap
从表1可以看出,信噪比间隔随着调制方式的改变变化并不是很大,对子信道功率分配的影响比较小,但其影响不容忽视。由式(4)可知,子信道比特分配与功率分配变化趋势一致,因此信道频域响应也是子信道比特分配的主要影响因素。
2 算法仿真
2.1 比特分配仿真结果
本文OFDM仿真模型:子载波个数N=256,循环前缀为64,调制方式M-QAM(M可以取值:2,4,8,16,32,64,128,256)。根据电缆特性变换频率,分析采用1个训练序列帧得出分配方案,其后3个有效信息帧直接应用该分配方案进行调制和解调,可以有效确保数据传输准确性。图2为比例贪婪算法在信道特性较差与较好时比特分配的仿真结果。

图2 比特分配结果Fig.2 Allocation results of bits
从图2可以看出,比特分配的结果和信道的频域响应变化趋势大体一致,但因有信噪比间隔的影响,还存在略微区别。信道特性比较好时,最高调制可以达到256QAM调制,但是信道特性较差时,每个子信道衰减较大,最高调制方式下降到64QAM。
2.2 对比分析
本文在对比例贪婪算法仿真的同时,将其与Chow算法和固定比特分配算法作比较,并计算出3种算法在不同信噪比条件下的误比特率,如图3所示。在相同的信噪比之下,比例贪婪算法误比特率介于固定比特分配算法和Chow算法之间[12-13],并且在SNR=35时大致衰减到10-4。
同时,以贪婪算法为参考,将该算法与Chow算法的计算量进行分析比较[14-15],如表2所示。

图3 各方法在不同信噪比下误比特率Fig.3 BER of each method at different SNRs

表2 算法计算量比较Table 2 Comparison of computational amount of algorithm
表2中,N代表子信道个数,S1代表比例贪婪算法最后几个比特分配时的迭代次数,S2代表贪婪算法逐比特分配的迭代次数,C代表在找到最佳余量前人为设置的迭代次数,S3为迭代结束后为使总比特数等于目标比特数而进行的搜索次数。由于比例分配过程已经分配了大部分功率,用贪婪算法逐比特分配的只剩下比特取整之后的小部分功率,所以S1值很小;贪婪算法每一比特都要迭代一次,所以S2等于分配的总比特数。通过3种算法计算量的大体估计,可以发现贪婪算法复杂度相当高,与比例贪婪算法和Chow算法不在一个数量级,而Chow算法一般迭代次数至少10次,计算量至少是比例贪婪算法计算量的3倍,如图4所示。

图4 算法计算量对比Fig.4 Comparison of computational amount of algorithm
3 结 语
电缆信道特性随时间变化速度比无线信道慢很多,因此本文提出一种适用于电缆信道系统的自适应比特分配算法——比例贪婪分配算法。在系统总功率和误比特率要求下,使系统传输速率达到最大。由于运用比例系数先分配大部分功率,该算法只在最后几个比特分配的过程中涉及迭代,计算量大大降低。并且之前的算法把信道比间隔视为固定值,忽略了其对功率分配的影响,该算法将信噪比间隔考虑在内,更准确地得到各个子信道的功率分配和比特分配。
