强冲击条件下铁路路基动态响应敏感度分析

吴卫民，马大为，朱忠领

（南京理工大学机械工程学院，南京 210094）

0 引言

近年来我国铁路得到飞跃的发展，铁路线纵横交错。在如此大而复杂的铁路系统中，铁路运行的安全尤为重要。在列车受到垂向强冲击载荷时，铁路路基受到较大的影响。

目前的方法是：在受到垂向冲击载荷时，用液压支腿将其加到铁轨上或者将其加到道床上。无论是哪一种的方式都会对路基产生较大的影响，导致铁路路基产生较大的变形，较高的应变率。而铁路路基内部的相互挤压的应力[1]作用使得各个材料产生不同程度的破坏。这样会影响稳定性和列车行驶的安全。结合目前公路场坪研究的进展[2-3]，研究方法主要为在显示动态计算，这种方法具有较大的建模难度，计算消耗时间较长，难以满足其快速高效的计算需求。

本文在研究铁路各层材料的特性、塑性损伤本构关系，建立了与铁路路基相对应的数值模型；通过试验设计以及响应面（RSM）模型方法，建立了高效计算模型；并且对其动态相应的主要因素进行敏感度分析。

1 数值模型的建立

本文对铁路路基进行研究[4-5]，路基从上往下依次为铁轨、轨枕、道床、基床表层、基床底层、基床以下路堤和地基。其中轨枕有一部分是嵌在道床里的，不同的深度将产生不同程度的影响。轨枕及其以下各个层的厚度为 H1，H2，H3，H4，H5，H6；相对应的每层材料的弹性模量分别用 E1，E2，E3，E4，E5，E6，铁轨采用国家标准的材料，用E0表示；轨枕在道床里的深度用H0表示，见图1所示：

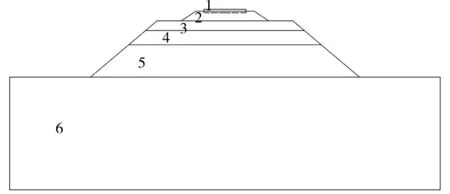
图1 铁路路基结构示意图

道床顶面的宽度为3.6 m，道床边的坡度取标准值1∶1.75。基床顶面的宽度为8.8 m，基床及基床以下路堤的边坡坡比取1∶1.5，地基深度取值20 m。轨枕[6-7]又称枕木，以前用的材料多为木材，现在改为混凝土。轨枕的作用是支撑钢轨以及保持钢轨的位置，同时把钢轨传递的巨大压力传递给道床。道床为轨道的重要组成部分，道床是指在轨枕下面、基床上面的石渣垫层，材料一般为级配碎石，道床的厚度为0.6 m。基床一般都分为基床表层和基床底层。道床下0.6 m为基床表层，表层下0.9 m为基床底层，其材料[8]分别为A、B组填料，其具体的弹性模量，泊松比以及密度见表1所示。

随机性和非线性是其受力的基本特征[9-10]，若采用线弹性模型则难以满足其计算要求。在处于动态响应时为提高其计算精度和效率，各层之间采用的是连续的形式进行模拟，而非连续层之间的力学特性则不予考虑[11-12]，路基底面设置为固定端约束，在此基础上建立铁路路基的数值模型见图2所示。

列车存在自身的重量，使得铁路路基受到稳态的载荷，故应给予初始应力场。并在此基础上对列车受到垂向冲击载荷时进行动态的仿真，其主要是研究路基位移相应的峰值，示意图见图3所示。

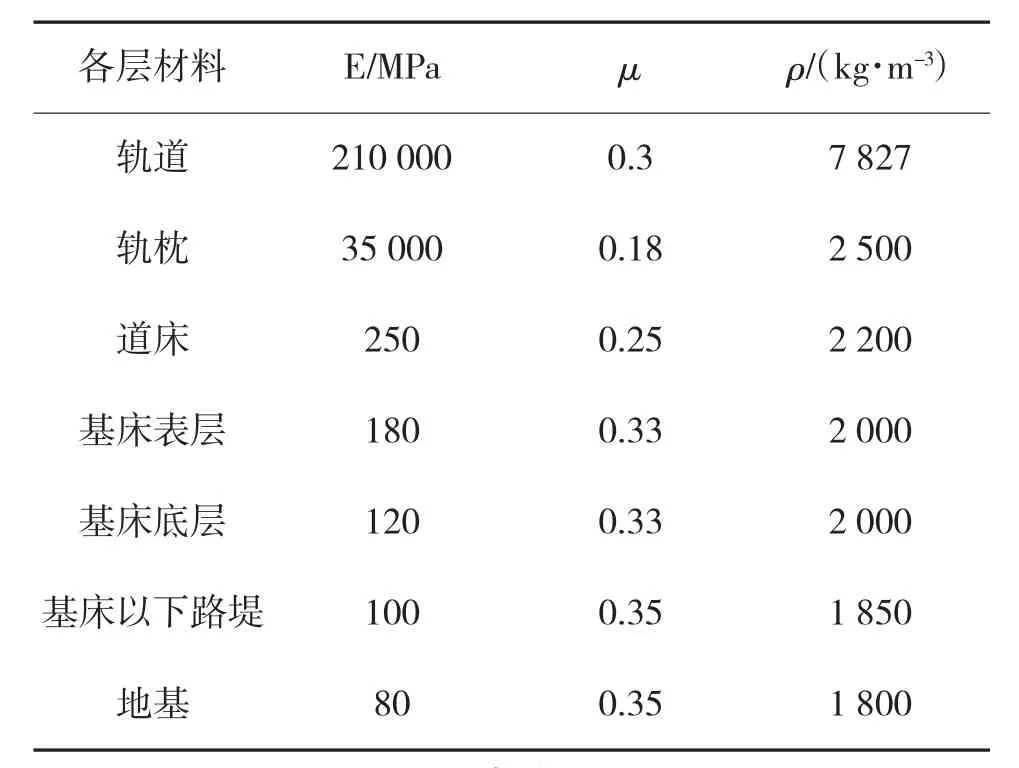
表1 各层材料的物理力学参数

图2 路基的数值模型

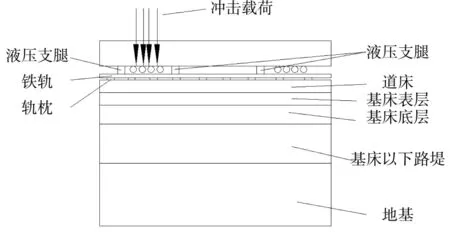
图3 受冲击载荷时的示意图

2 近似模型的建立

建立近似模型其实就是利用相对较简单的近似函数来代替实际的模型。由于模型比较复杂，近似模型正确的建立可以提高计算的精度和减少计算的时间。为了在较短的计算时间内得到更精确的近似模型，在建立近似模型前，先采用拉丁超立方设计方法对数据进行采样。

2.1 近似模型

铁路的路基由道床、基床表层、基床底层、基床以下路基和地基各部分组成。其密度、弹性模量、泊松比和厚度的数值如表1所示，把其弹性模量和材料的厚度作为输入变量，根据实际的路基情况给出了其变化的范围，如表2所示。

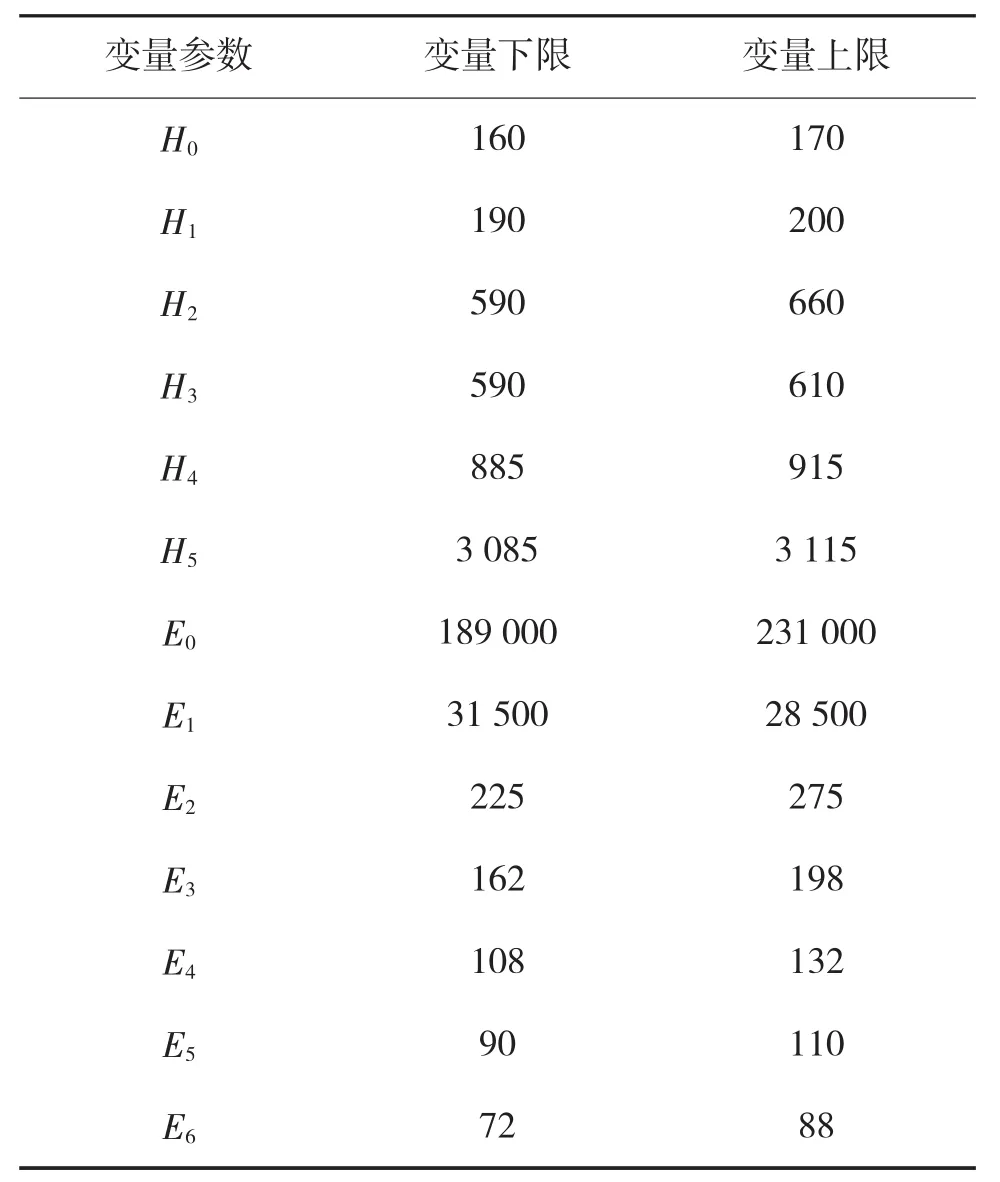
表2 参数变化范围

为了提高精确度和准确性，尽量使铁路路基位移变形较小，增大其稳定性。故此选择路基响应的位移峰值作为所建立的近似模型的输出参数。为了提高建立近似模型的准确性，选取100个数据组作为样本建立近似模型，其流程图见图4所示。

图4 近似模型的建立流程图

2.2 模型的验证

由于非线性和变量的个数是影响近似模型的拟合效率和拟合精度的主要因素，用近似值和真实值之间的差异程度（r）检验拟合的精度，其定义为：

式中：ne为模型误差验证的样本点数；yg为真实的相应值；为近似模型的观察值；y为真实相应的均值；其中r值越小表示近似模型的拟合度越高。

近似模型总方差主要是由近似模型本身和拟合误差组成的。方差分析采用离均差平方和（S2）

式中：yg表示第g个样本的真实值；y表示样本y点的均值；表示近似模型第g个样本点的相应值；R2近似模型的拟合精度；

R2值越接近1，表明拟合模型越精确。本文中的R2=0.98，接近1，故此可以认为所建的近似模型较为准确，见图5所示。

图5 近似模型误差分析

3 动态位移响应影响因素的敏感度分析

3.1 影响位移响应的因素

将影响移响应的参数整理，归一化等处理，可以得出其主要影响因数和次要影响因数。其处理后的数据结果见下页表3。表中的，式中的U0为原模型中的位移响应最大值；U为在其参数去极限时的位移响应值。

由表3的结果可以看出各个因素的变动对路基位移响应的影响，其中E6，E5和H2对位移响应的影响较大。故此可以认为E6，E5和H2为位移响应的主要因素。

表3 位移响应结果

3.2 主要因素的敏感度分析

根据结果显示E6，E5和H2为影响路基位移响应的主要因素。先取这3个主要因素按照一定比例增长的数值，并带入近似模型中，得出路基位移响应变化比例S与影响因素的取值变化比例T的关系，见图6。通过分析得出E6对路基位移的影响最大，其次是E5，在3组中H2对位移影响最小。E6为地基的弹性模量，宏观上可代表地基的软硬程度，故有载荷作用时其敏感度最大；E5为基床以下路基，其敏感度也较大；H2为道床的厚度，当H2增大时，载荷的传递距离也变大，受力面积增大，故路基位移减小。当3组数据进行横向对比时，可以发现3组数据中的E5和E6的变化范围比例大小相等。但在相同比例下，E6对路基的敏感度值大于E5对路基的敏感度值。并且可以发现H2变化范围最小，其敏感度也最低。综合分析这3组因素对路基动态响应的敏感度为 E6＞E5＞H2。

3.3 次要因素的敏感度分析

利用同样的方法对其次要因素的敏感度进行分析，选取 E4、H3、E2和 E3进行横向分析，其弹性模量E和厚度H均与位移响应呈反比，见图7所示。

E2为道床的弹性模量，E3为基床表层的弹性模量，E4为基床底层的弹性模量，H3为基床表层的厚度，对这4组次要因素进行横向比较，得出其位移响应的敏感度为 H3＞E4＞E2＞E3。

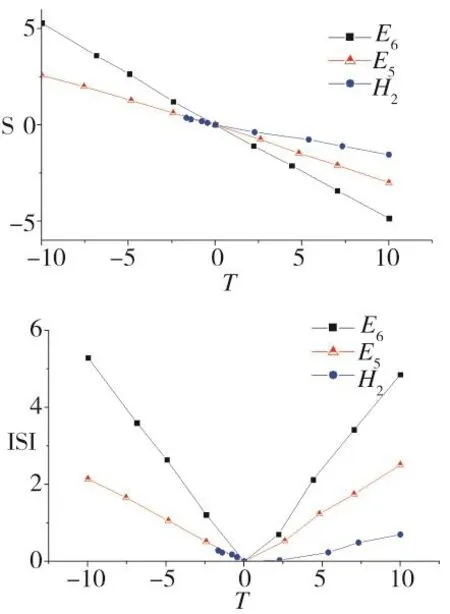
图6 主要因素的敏感度分析

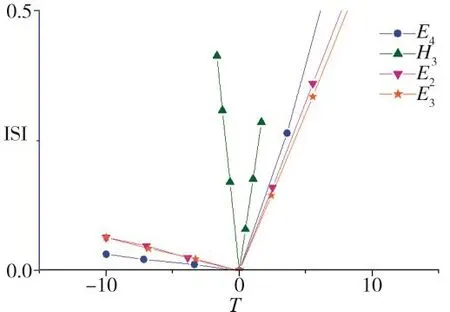
图7 次要因素的敏感度分析

4 结论

通过改变铁路路基各层的参数，得到影响位移响应的各个因素并对其加以分析，得到以下结论：

1）所建立的近似模型的误差主要是来源于近似模型本身以及拟合误差。结果表明近似模型的结果D与计算所得的结果D0相对误差的最大值为0.58%，并且得到拟合精度达R2=0.98，故所建立的近似模型默认为正确可行的；

2）铁路路基各层材料弹性模量的参数以及厚度均与响应位移呈反比，其主要的影响因素为E6、H2和 E5，并且其敏感度的排序为 E6＞E5＞H2；

3）E4、H3、E2和 E3为次要的影响因素，弹性模量E和厚度H均与位移响应呈反比，这4组的敏感度影响顺序为 H3＞E4＞E2＞E3。

本文初步对铁路路基的敏感度进行了分析，对铁路受垂向冲击载荷时，铁路路基的响应具有一定的意义，为路基的设计与优化提供了支撑。