基于兰切斯特方程的战斗时滞分析

杨戈方

（陆军边海防学院，昆明 650207）

0 引言

我国古代的《汉书·项籍传》和现代一些军事强国以及我周边的一些国家都提出先发制人的战略思想；现代高技术战争，强调“先敌发现，先敌打击，先敌压制”，其深刻的作战机理必须引起我们的高度重视。先发制人的战略思想主要体现是当战争开始时，使敌方延迟一段反应时间，己方先动而谋优势，先动制敌于死地。先发制人的战略思想在定量的分析中，主要在文献[1-6]中有过一些研究，其主要的方法是利用改进的兰切斯特方程或者时滞的兰切斯特方程对作战其中的一方进行延迟一段反应时间，即战斗时滞，用解析法、数值计算以及仿真模型计算等方法研究双方的交战，得到先发制人的定量研究结果，但是这些研究还不够全面，未给出一般条件，个别还存在不严密的地方。同时，对后发制于人的战略思想还没有见到定量研究，在《荀子·议兵》、《孙子兵法》和毛泽东军事思想中有专门的后发制人论述，古今中外的很多战例都是运用后发制人战略思想的典范。为了更加全面地研究先发制人和后发制人的作战机理，运用兰切斯特方程进行解析分析，从弱势的一方对先发制人以及后发制于人的战略思想进行更为深入和全面的分析研究，给出迟滞时间的一般条件。

1 建立兰切斯特方程

1.1 兰切斯特方程

设红蓝双方进行对抗战斗，可建立以下兰切斯特方程[7-9]：

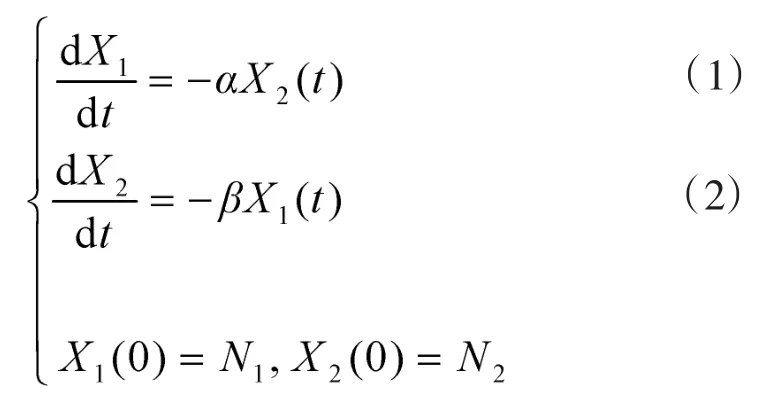
1.2 兰切斯特方程的求解

1.2.1 平方律

式（1）除以式（2）得：

解得：

式（3）也可以写为：

由平方律知：谁初始战斗力大，谁就取胜。

1.2.2 兰切斯特方程的解

对式（1）两边求导得：

将式（2）带入式（4）得：

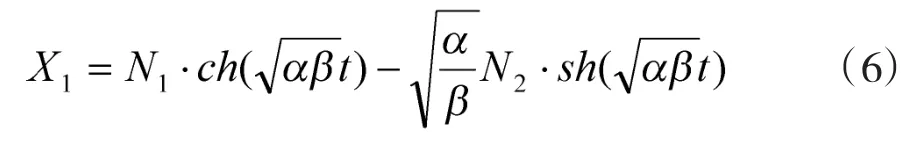
2 兰切斯特方程的战斗时滞分析

2.1 先发制人情况下兰切斯特方程战斗时滞时间

假设红方先发制人，在战斗刚开始，迟滞蓝方T个时间单位，即在这T个时间单位内，α=0，并且，则兰切斯特方程为：

解得：

即当红方先发制人，红方迟滞蓝方的时间T满足式（8）时，红方可获得胜利。

2.2 后发制人情况下兰切斯特方程战斗时滞时间

假设红方后发制人，当红蓝双方战斗T1个时间单位后，红方再迟滞蓝方T个时间单位，即在这T个时间单位内，α=0，并且。

在T1、T时刻时，由式（6）得红方初始兵力均为：

在T1时刻时，由式（7）得蓝方初始兵力为：

由兰切斯特方程：

解得：

红方要战胜蓝方，则在T时刻的红方初始战斗力必须大于蓝方初始战斗力，即：

解得：

即当红方后发制人，红方迟滞蓝方的时间T满足式（9）时，红方即可获得胜利。

2.3 先发制人情况下兰切斯特方程战斗时滞时间小于后发制人情况下战斗时滞时间

定理 1：由 2.2的式（8）、式（9），当 T1≠0则有：

定理 2：当 T1=0时，式（9）即为式（8）。

以下进行定理1的证明。

定理1证明：

由式（8）、式（9）得：

即：

即证：

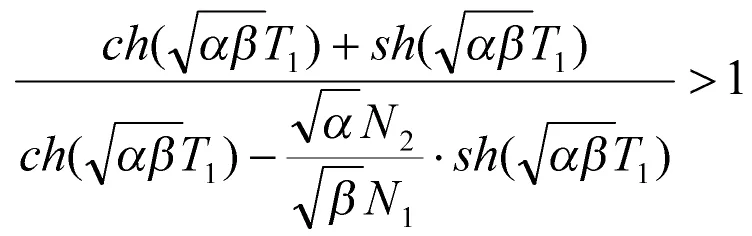
即：

定理2证明：略。

3 算例

根据以上得到的先发制人和后发制人的迟滞时间的条件式（8）和式（9），下面通过4个算例分析说明。这里运用MATLAB[10]画出红蓝双方战斗对抗兵力变化的X1，X2的图像，即兵力变化图1～图4。其中，由“*”画出的线是红方兵力变化曲线；由“.”画出的线是蓝方兵力变化曲线。

3.1 先发制人算例

例1设α=0.9，β=0.4，N1=10，N2=10，T=0.8，由2.1中的条件知，在红方先发制人的条件下，要使红方战胜蓝方，T必须满足式（8）。

因为：

所以在红方先发制人的条件下，蓝方战胜红方。如图1所示。

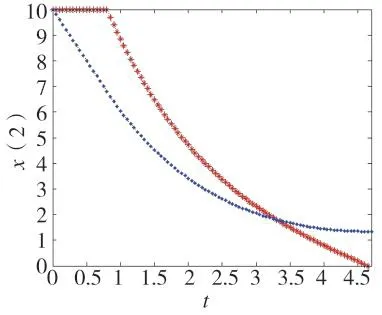
图1 当T=0.8时战斗双方兵力变化图

例2设 α=0.9，β=0.4，N1=10，N2=10，T=0.9，由2.1中的条件知，在红方先发制人的条件下，要使红方战胜蓝方，T必须满足式（8）。

因为：

所以在红方先发制人的条件下，红方战胜蓝方。如图2所示。

图2 当T=0.9时战斗双方兵力变化图

从例1和例2看出，先发制人条件下，迟滞时间的不同导致胜负结果的不同。即使红方初始战斗力弱于蓝方，只要迟滞时间T满足式（8），红方即可获得胜利。

3.2 后发制人算例

例3设 α=0.9，β=0.4，N1=10，N2=10，T1=0.2，T=1.1，由2.2中的条件知，在红方后发制人的条件下，要使红方战胜蓝方，T必须满足式（9）。

因为：

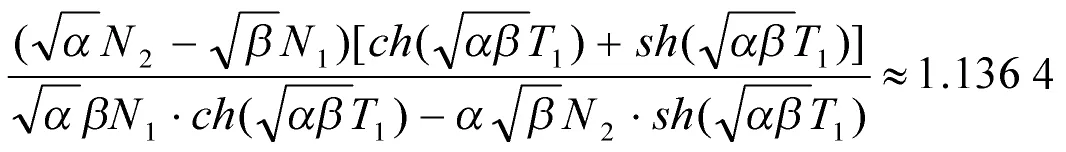
所以在红方后发制人的条件下，蓝方战胜红方。如图3所示。

图3 当T1=0.2，T=1.1时战斗双方兵力变化图

例4设α=0.9，β=0.4，N1=10，N2=10，T1=0.2，T=1.3，由2.2中的条件知，在红方后发制人的条件下，要使红方战胜蓝方，T必须满足式（9）。

因为：

所以在红方后发制人的条件下，红方战胜蓝方。如图4所示。

图4 当T1=0.2，T=1.3时战斗双方兵力变化图

从例3和例4看出，后发制人条件下，迟滞时间的不同同样导致胜负结果的不同。即使红方初始战斗力弱于蓝方，只要迟滞时间T满足式（9），红方即可获得胜利。

从例2和例4看出，在相同的条件下，先发制人和后发制人在迟滞时间分别满足式（8）和式（9）时，红方均获得胜利，但是先发制人情况下的最小迟滞时间要小于后发制人情况下的最小迟滞时间，符合2.3中的定理1。

4 结论

运用兰切斯特方程对战斗时滞的时间、时刻进行了分析研究，根据推导，给出了弱势一方的先发制人和后发制人的一般条件。根据一般条件，弱势一方在先发制人或者是后发制人的情况下，对不同的具体条件的战斗情况，可以求出迟滞的不同时间，为军事训练和作战决策提供定量分析的手段和依据。这里仅讨论了一方的战斗时滞，而且是被压制方在被压制的时间段内无任何反击能力，还可以讨论双方交替的战斗时滞，以及被压制方在被压制的时间段内有一定反击能力的情况，以上各种情况，有待更深入的研究。