认知雷达网联合传感器选择和功率分配*
2018-11-13俞晓波郭宝峰
俞晓波,左 燕,郭宝峰,谷 雨
(杭州电子科技大学信息与控制研究所,杭州 310018)
0 引言
认知雷达系统通过接收端感知周围环境,并将信息反馈至信息处理中心,并结合先验信息自适应地调节雷达发射端和接收端的资源配置,以提高系统的整体跟踪性能[1]。发射端目标探测和接收端信息处理方式以协作的方式构成一个动态闭环的认知雷达系统[2]。认知雷达网络利用多个认知雷达协同工作来完成增强远程探测能力的任务,相比于单雷达大大提高了跟踪性能和定位能力。在认知雷达的发展过程中,如何合理分配雷达网络内有限的传感器资源,充分发挥传感器的认知能力,最大限度地获取所需目标信息提升跟踪性能已成为军事领域研究的重点。
文献[3]给出了多雷达目标定位估计均方根误差(MSE)的全局后验克-拉美罗下界(PCRLB)。随后,文献[4]推导了多雷达系统目标跟踪问题下运动目标的位置和速度估计MSE的PCRLB。以上分析结果指出,多雷达系统的目标定位和跟踪精度与雷达数目,雷达带宽,信噪比(SNR)相关。而SNR与雷达的发射功率、衰减因子、雷达散射截面积有紧密关系[5]。因此,理论上增加认知雷达系统中雷达数目和雷达发射功率,均可以达到提升系统跟踪性能的效果。在实际的应用场合中,考虑到组网内有限的雷达探测资源,如机载监视雷达装备电池,雷达的发射功率有限。同时考虑多目标和计算负载,对雷达系统内的传感器进行合理分配具有重要意义[6]。
传感器资源管理的核心是基于某一优化准则对传感器资源进行合理科学的分配[7]。在目标跟踪问题中,PCRLB定义为Fisher信息矩阵的逆,它给出了目标状态估计可实现的最佳精度的下界[5]。该指标不依赖于目标跟踪的具体滤波算法,而且具有较低的计算复杂性[8],因此,可以把它作为一种较好的雷达资源分配的优化准则。文献[8]将目标跟踪误差的克-拉美罗下界(PCRLB)指标引入协同跟踪模型,进行目标传感器优化分配。文献[9]给出了多目标跟踪下基于PCRLB的传感器分配策略。文献[10]研究了分布式网络结构下基于PCRLB的传感器分配问题。文献[11-12]在分布式多输入多输出(MIMO)雷达的平台下,提出了基于PCRLB的功率分配方法。将目标定位误差的PCRLB作为功率分配的函数,通过优化分配雷达的发射功率,使目标的定位精度最高。文献[13-14]研究目标跟踪下基于PCRLB的雷达功率分配问题。文献[15]在认知雷达框架下,提出了多目标跟踪的传感器和功率的联合分配问题,将该问题凸松弛后采用贪婪算法进行求解。
上述研究均以PCRLB为优化准则进行资源分配,然而文献[8-14]假设每部雷达以平均功率发射信号,通过选择最佳传感器组合提高目标跟踪性能,文献[11-14]假设系统中所有雷达参与跟踪,通过优化各部雷达的功率提高跟踪精度,传感器选择和功率分配联合优化可以进一步合理利用有限资源,提升目标跟踪性能。文献[15]同时考虑联合传感器选择和功率分配问题,采用贪婪算法求解优化问题,无法获得最优解[14]。本文在多认知雷达框架下,提出了一种基于PCRLB的认知雷达系统联合传感器选择与功率分配算法,同时结合凸松弛和循环最小算法对该问题进行求解,最后的仿真证明优化后的传感器组合方式和功率分配方案提高了目标的跟踪精度。
1 问题描述
1.1 目标运动模型
假设N个空间分离的运动目标在二维空间中做匀速运动,k时刻第q个目标的运动模型可描述为

其中,xqk表示 k时刻第q个目标的状态,,和分别表示k时刻第q个目标的位置和速度;目标状态转移矩阵,其中T表示采样周期;为k-1时刻零均值的白色高斯过程噪声,其协方差矩阵,ρ为过程噪声参数[16]。
1.2 测量模型

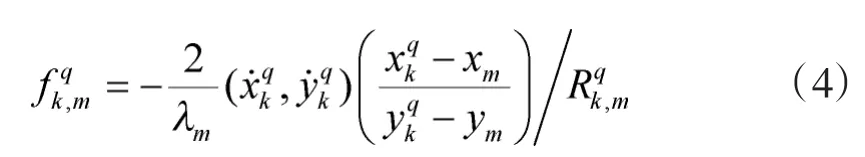
其中,λm表示第m部雷达的工作波长。
在实际中,雷达的测量往往含有随机误差。在k时刻,第m部雷达测量第q个目标得到的实际距离、方位角和多普勒信息分别为


考虑到在实际场景中每部雷达都有固有的跟踪能力,因此,在每一时刻需要选择参与跟踪的最佳传感器集合。定义传感器选择集合,它表示在k时刻被选中参与跟踪第q个目标的雷达子集。

多雷达系统第k时刻对第q个目标的测量集合可表示为



式(11)中量测方差根据式(6)计算。
2 基于PCRLB的多雷达系统联合传感器选择和功率分配
2.1 后验克-拉美罗下界(PCRLB)推导
PCRLB定义为Fisher矩阵的逆,给出了目标状态估计误差的协方差矩阵的一个下界,即无偏估计量
必须符合下面的要求[16]:

J表示为Fisher矩阵,并且

文献[17]提供了单目标贝叶斯信息矩阵J的迭代求解方法,以此类推,可以推导第q个目标的Fisher信息矩阵如下所示:

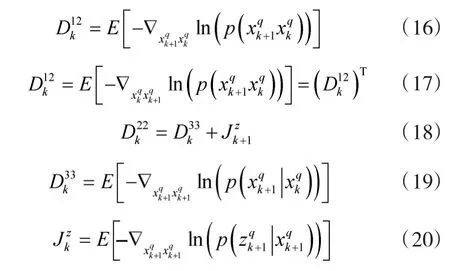
本文中,根据式(1)提供的运动模型和式(9)提供的量测模型,推导可得


PCRLB定义为Fisher矩阵的逆,本文研究联合传感器选择和功率分配问题,决策变量包括传感器组合方式

由式(25)和式(26)可知,PCRLB 给出了目标状态估计误差的下界,它为目标跟踪精度提高了一种有效的度量指标。PCRLB的计算不依赖于具体跟踪滤波算法,而且具有一步预测能力,具有较低的计算复杂性[8]。
2.2 基于PCRLB的联合传感器选择和功率分配优化算法
由式(25)和(26)可知,PCRLB 指标是传感器组合和雷达发射功率Pk的函数。以PCRLB的迹为代价函数,在满足各部雷达发射功率约束和雷达跟踪能力约束的前提下同时优化最佳传感器组合和功率分配,可以实现目标跟踪状态估计误差下界最小,提高目标的跟踪性能。本文以PCRLB为代价函数,对传感器和功率进行联合分配,结合凸松弛和循环最小算法对双变量非凸优化问题进行求解。
2.2.1 基于PCRLB的联合传感器选择和功率分配模型
由式(25)和式(26)可知,多雷达组网跟踪下各个目标的PCRLB的计算相互独立。在多目标跟踪情况下,要求确保任何一个的目标跟踪误差都不太大。因此,下一时刻不同组合方式和功率分配目标函数可定义为

在实际中,受通信带宽,传输速率和计算复杂性的限制,设定同一时刻最多只有L部雷达能够同时跟踪同一个目标,且每一部雷达跟踪能力有限,每部雷达只能同时跟踪η个目标。同时,考虑雷达的发射总功率能力有限,且每部参与跟踪的雷达发射功率限制在最大发射功率Pmax和最小发射功率Pmin之间。
在满足上述各部雷达发射功率约束和雷达跟踪能力约束的前提下,通过优化传感器组合和功率分配,实现目标状态估计误差PCRLB指标最小,建立优化模型如下:

2.2.2 凸松弛和循环最小化联合求解算法
基于PCRLB的联合传感器选择和功率分配模型是一个包含两个变量的非凸优化问题,本文提出结合凸松弛和循环最小算法对双变量优化问题进行求解,具体的流程如下所示:
步骤1功率均匀分配下的传感器(雷达)选择:

将指定的 Sk,opt代入式(27),可以得到功率分配问题(29)

采用单纯形算法求解,在多项式时间内获得参与跟踪的最佳传感器组合。由于决策变量整数的条件被松弛,选择优化结果中前L个最大的元素将其置为1,并将其余元素置0,生成次优选择子集Sk,opt,这时得到的 Sk,opt就是均匀分配下最佳的传感器组合方式。
步骤2给定传感器选择Sk情况下的雷达功率分配。
对上述凸优化问题(30),采用梯度投影法[18](见表1)求解,得到功率分配的最佳结果Pk,opt。
步骤 3 根据得到的 Sk,opt和 Pk,opt,计算出相应的目标函数值F(Sk)。将最佳功率分配结果返回,转步骤(1);上述过程迭代,直至前后迭代获得的目标函数值不再下降为止。
通过上述迭代算法,可以获得最佳的传感器组合方式和功率分配方案。

表1 梯度投影法
3 仿真结果与分析
为了验证本文所提算法的有效性,本节对在两种不同雷达布阵方式下的机动目标进行仿真。本文所提供的雷达场景中共包含6个独立的雷达,2个机动目标,即M=6,N=2。假设在同一时间对同一个目标进行跟踪的最大雷达数目L=2,且每部雷达的跟踪能力均为η=1。在整个监视期间,本文一共使用了12帧采样间隔T=6 s的数据用于仿真。假设每部雷达的工作参数一致且每个目标的初始位置和速度已知。雷达发射信号的有效带宽βm=1 MHz,相参脉冲个数Tm=32,工作波长λ=0.3 m,发射功率的上下界被设置为Pmin=0.01Ptotal和Pmax=0.6Ptotal。
下页图1给出了两个场景下雷达与机动目标的相对空间位置,场景1中,两个目标的初始状态分别为和,场景2中,两个目标的初始状态分别为和。图2中,无优化分配是指在雷达系统跟踪机动目标过程中,固定跟踪每个目标的雷达传感器子集,并且对被选中的雷达平均分配功率。由图2可知,通过联合传感器和功率优化分配算法之后得到的PCRLB与雷达资源无优化分配时相比明显减小,跟踪精度得到很大的提高。图2中(a)与(b)相比较,图(b)中的PCRLB明显下降更多,第2种雷达布阵方案下的雷达优化分配更好,说明雷达精度的提升幅度与雷达布阵有紧密关系。

图1 雷达与机动目标之间的位置关系

图2 目标跟踪的PCRLB变化

图3 传感器选择方式

图4 雷达功率分配情况
图3表示各个时刻雷达传感器的组合方式。以图3(a)为例,在 1≦k≦4,目标 1开始运动,1号和 2号雷达与目标的相对位置更好,所以选择1号和2号雷达进行跟踪。在5≤k≤10,目标1继续运动,3号雷达相对1号雷达的位置更好,所以代替1号雷达进行跟踪。在仿真的最后,相对于目标1的位置,6号雷达较2号雷达更好,所以代替2号雷达完成跟踪。由此得出结论,与目标的相对位置越好的雷达会被系统选中参与目标跟踪。
图4给出了被选中参与目标跟踪的雷达发射功率经过优化后分配情况,以图4(a)为例,在k=3时刻,1号和2号雷达对目标1进行跟踪,但2号雷达和1号雷达相比,与目标的相对位置更差,但是显然2号雷达分配到了更多的发射功率。由此从得出结论可以看出在跟踪同一目标的2部雷达里,系统倾向于分配更多的功率给相对位置更差的雷达。
4 结论
本文在认知雷达系统平台下,提出了一种目标跟踪下基于PCRLB的多雷达系统联合传感器选择和功率分配方法。首先推导了认知雷达系统目标跟踪下全局后验估计的克-拉美罗下界,该指标用于度量目标的跟踪精度。随后以PCRLB的迹为代价函数,构建基于PCRLB的联合传感器选择和功率分配模型。对于构建的非凸优化问题,设计了基于凸松弛的循环最小化算法。仿真结果证明,相比于雷达资源无优化分配方案,通过联合传感器选择和功率分配算法优化后的跟踪性能明显提升。本文考虑的传感器位置是固定不变的,机载雷达的路径优化对目标定位跟踪性能影响较大,飞机路径优化和雷达资源分配的联合优化是今后研究的重点。
