菱形截面T型触探探头贯入阻力研究
2018-11-12
(中国电力工程顾问集团华北电力设计院有限公司,北京 100120)
T型触探也叫全流触探,是原位测试软黏土不排水抗剪强度的一种方法。近年来在海域极低强度软黏土的原位测试中得到应用。Stewart和Randolph将T型触探应用到工程现场软黏土不排水抗剪强度测试中。国内王冉冉采用室内试验和离心机试验,对探头尺寸、贯入速率等影响因素进行了研究,与十字板试验、圆锥贯入仪等测试手段进行了对比。Zhou和范庆来等采用数值模拟方法研究了贯入速率、地基土强度各向异性及其软化效应的影响。
传统T型触探探头截面为圆形,测试结果解译有严格的理论依据,测试效率高,能得到沿深度的连续不排水抗剪强度值,但测试结果受探头表面粗糙度的影响较大,对应于完全光滑和完全粗糙两种极限条件,测试结果差值与均值比达26%。实际工程中,受加工以及现场磨损的影响,很难控制探头的粗糙度,一定程度上限制了该试验方法的应用。采用其它形状探头的触探仪,以减小系统误差,一直是工程和学术界努力研究的方向。
基于极限分析原理,本文求得了菱形截面探头阻力的精确解,分析了系统误差随菱形轴长比的变化,找到了最优的轴长比区间,得到了菱形截面探头工作所需的计算参数,提出了具体工作方法。
1 基本假设
设无限长菱形截面探头长半轴长为a,短半轴长为b。探头位移方向为y,位移速度为V0,位于充满软黏土的无限空间内(图1)。软黏土不排水抗剪强度为Su。
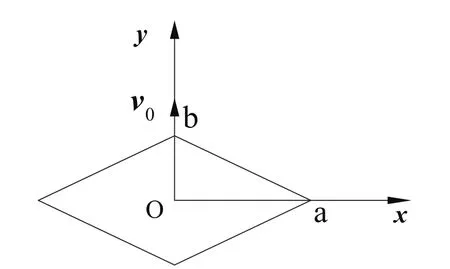
图1 探头剖面及位移
为了求得图1所示条件下探头贯入阻力系数,采用两项假设:(1)软黏土强度服从Tresca屈服条件,仅有不排水抗剪强度Su一个指标;(2)探头为无限长杆,匀速压入土中,可简化为平面应变问题。探头贯入过程中,软黏土只产生局部塑性变形,无排水发生,体积保持不变,满足理想刚塑性体的Tresca屈服条件,根据极限分析法可以得到较可靠的结果。
探头土界面土单元的摩尔应力圆见图2。当土单元处于极限状态时,滑移线与探头表面的夹角为。其中,sinΔ=λ。对于粗糙和光滑状态,滑移线与探头表面的夹角分别为0和。
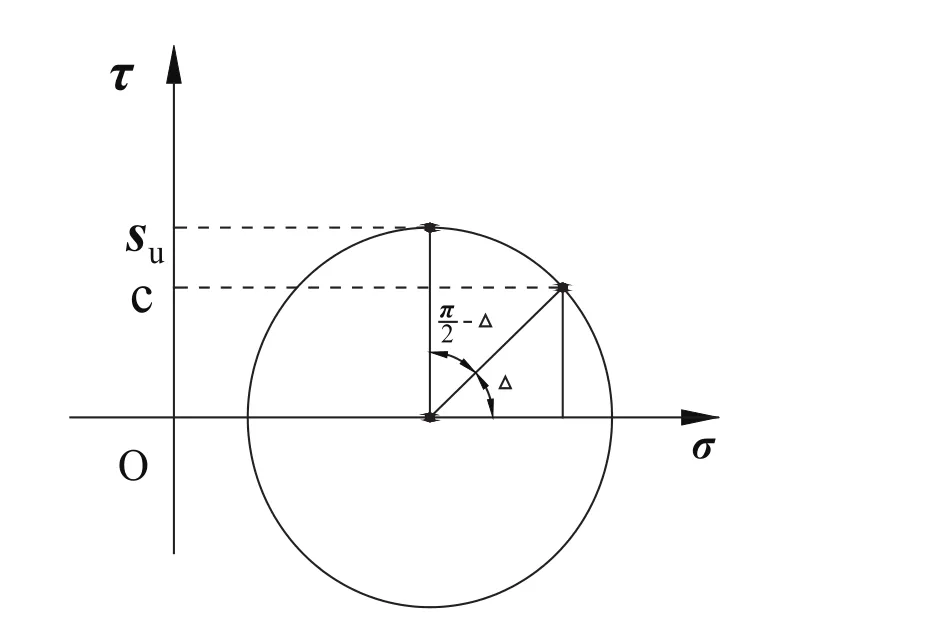
图2 探头土界面土单元摩尔应力圆
根据图2,得到探头表面与周边土体之间的粘着力c与不排水抗剪强度有如下关系:

式中:λ为探头表面粗糙度,0≤λ≤1。当λ=0时,表示探头表面光滑;当λ=1时,表示探头表面粗糙。
为简洁起见,本文只分析表面粗糙和光滑2个极限条件。极限条件下滑移线场见图3。
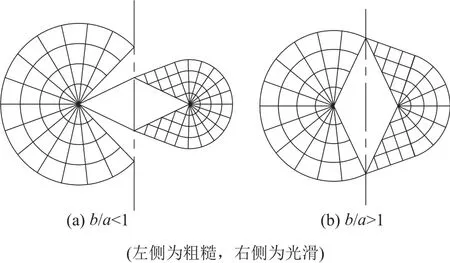
图3 极限条件下滑移线场
2 下限解
2.1 粗糙条件
当b/a<1时,根据图3所示滑移线场,粗糙条件下的变形机制见图4。在第Ⅰ象限内形成三角形刚性核ABQ,该区域内土体无相对滑移发生,与探头一起运动。BCDQ区域为同心圆柱壳区域,中心为Q点,相互转动的角速度随半径的增大而减小。BQ线与x轴的夹角为π/4。
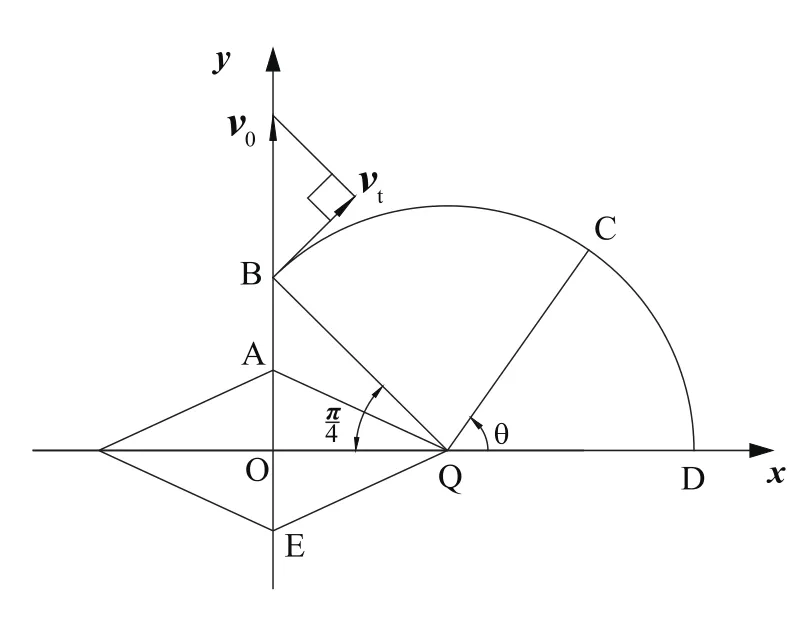
图4 粗糙条件变形机制(b/a<1)
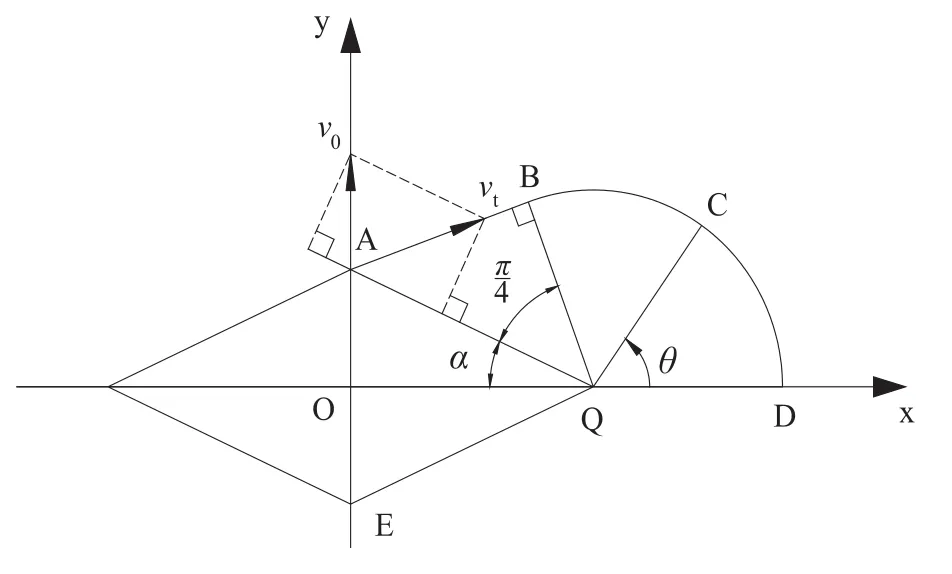
图5 光滑条件变形机制
设菱形水平中心线深度处的平均应力为σ0。对于第Ⅰ象限,QD线上平均应力为σ0。根据滑移线性质,QC线上的平均应力为σ0+2Suθ,QB线与QD的夹角为3π/4,QB线上的平均应力为σ0+3/2 πSu。QB线所受阻力在垂直方向上的分量为PQBnⅠ:
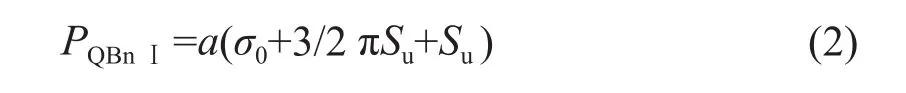
同理,第Ⅳ象限QE线上的平均应力为σ0-3/2πSu。则QE线所受阻力在垂直方向上的分量PQEnⅣ(与运动方向相同为负,下同)为:
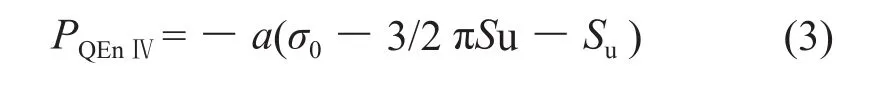
根据对称性,粗糙条件下,对于b/a<1的菱形探头,其运动过程中所受阻力下限解为:
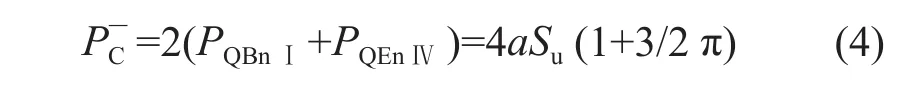
与b/a<1相似,求得b/a>1的探头阻力下限解:
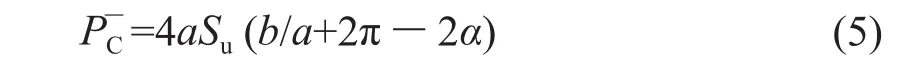
式中 :α=atanb/a。
2.2 光滑条件
根据图3所示滑移线场,光滑条件下的变形机制见图5。在第Ⅰ象限的滑移线场由均匀应力场ABQ和同心圆柱壳区域BCDQ组成。BQ线与菱形探头边线QA的夹角为。
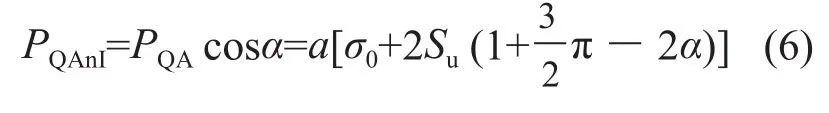
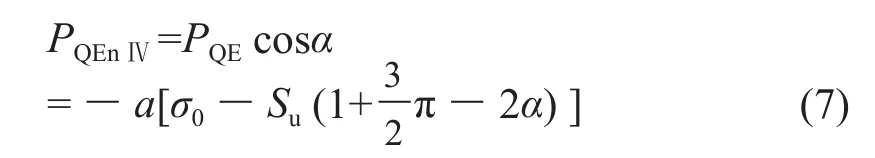
根据对称性,光滑条件下,菱形探头运动过程中所受阻力下限解为:
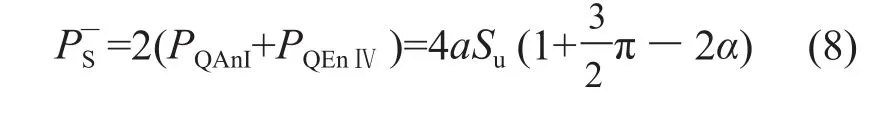
3 上限解
3.1 粗糙条件
对于b/a<1的菱形,根据图4的变形机制,QB线的速度曲线BCD以外土体的速度为0,BCD曲线以内,土体运动速度为vt,方向与区域内直线滑移线相垂直。Q点为奇异点。刚性区ABQ区域内无相对滑移。
设速度间断线BCD的长度为LBCD,间断线两侧的相对速度其内能消散率为ΔWBCD:
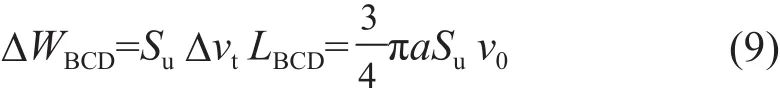
设同心圆柱区半径QB的长度为LQB。可以认为该区域是由无数条长为LQB,两侧为相对速度Δvtdθ的速度间断线窄条组成。则QBCD区域内的内能消散率为ΔWQBCD:
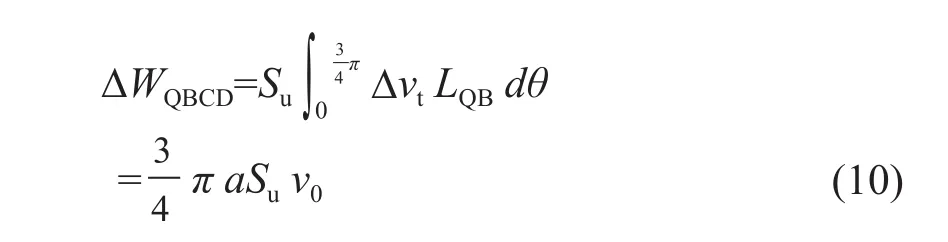
速度间断线QB线上的内能消散率ΔWQB为 :
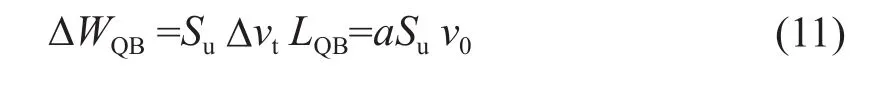
并将以上3部分内能消散率加在一起,并考虑到对称性,可得到总的内能消散率W为:
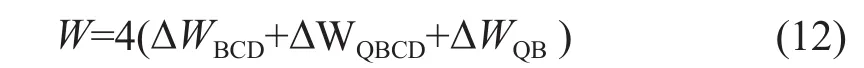
外功率等于菱形探头阻力PC+与速度v0的乘积。外功率与内能消散率二者应相等。由此得到粗糙条件探头阻力上限解PC+:与b/a<1相似,对于b/a>1的菱形,得到粗糙条件探头阻力上限解PC+:对比式(4)和式(13),式(5)和式(14)可知,探头阻力下限解与上限解PC+相同,所得阻力为精确解。
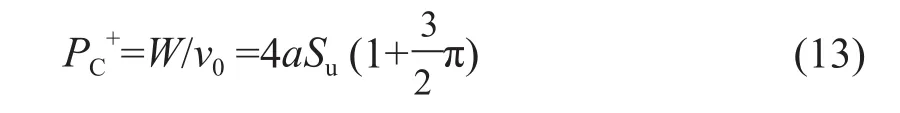
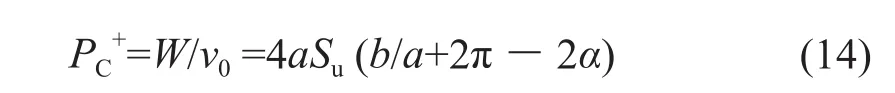
3.2 光滑条件
设速度间断线AB的长度为LAB,间断线两侧的相对速度其内能消散率ΔWAB为 :
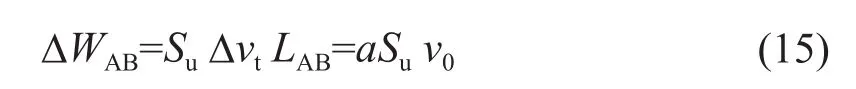
设速度间断线BCD的长度为LBCD,间断线两侧的相对速度其内能消散率ΔWBCD为:
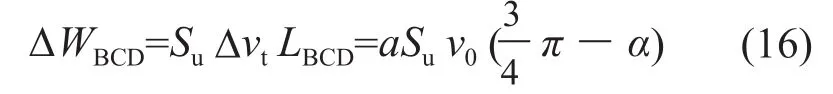
设同心圆柱区半径QB的长度为LQB。可以认为该区域是由无数条长为LQB,两侧为相对速度Δvtdθ的速度间断线的窄条组成。则QBCD区域内的内能消散率ΔWQBCD为:
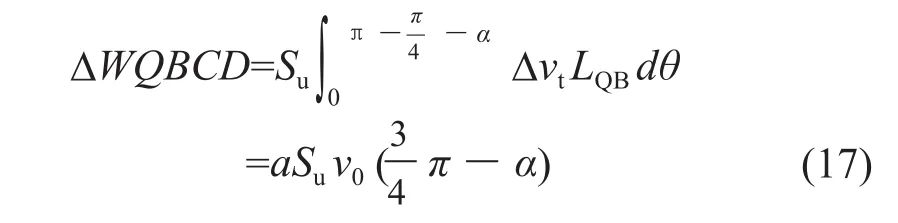
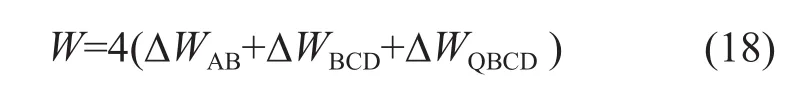
并将以上3部分内能消散率加在一起,并考虑到对称性,可得到总的内能消散率W为:外功率等于菱形探头阻力PC+与v0速度的乘积。外功率与内能消散率二者应相等。由此得到光滑条件探头阻力上限解PS+:
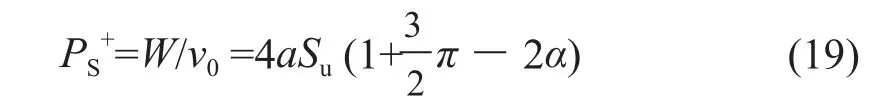
对比式(8)和式(19)可知,探头阻力下限解与上限解相同,所得阻力为精确解。
4 上下解对比与分析

表1 不同条件下菱形探头阻力系数
从探头使用看,表面光滑与粗糙条件下,阻力系数差值越小越好。为此,绘制光滑与粗糙两种条件阻力系数差值与阻力系数平均值之比随轴长比的变化曲线(见图6)。
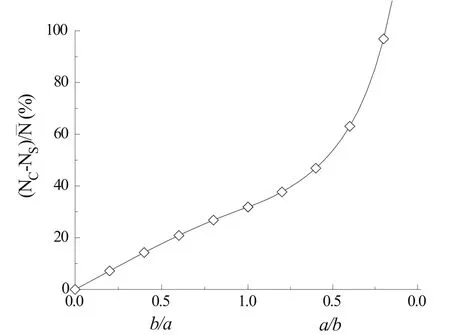
图6 阻力系数差值与平均值之比
从图6看出,菱形截面探头阻力系数差值与平均值之比,随着轴长比b/a的减小而减小,系统误差减小。当轴长比为0.8时,菱形截面探头阻力系数差值与平均值之比为26%,与传统圆形截面探头相当。考虑探头强度和变形影响,轴长比可取0.5。当轴长比取0.5时,菱形截面探头阻力系数差值与平均值之比为13%,明显优于圆形截面探头。
5 实施方式
工程实践中,菱形截面探头与静力触探仪探头的连接可采用锥槽式和丝扣式两种方式连接。
见图7,锥槽式在菱形截面探头侧面中部设置一顶角为60°的圆锥形容置槽。测试时,双桥静力触探机探头与菱形截面探头容置槽相切合。
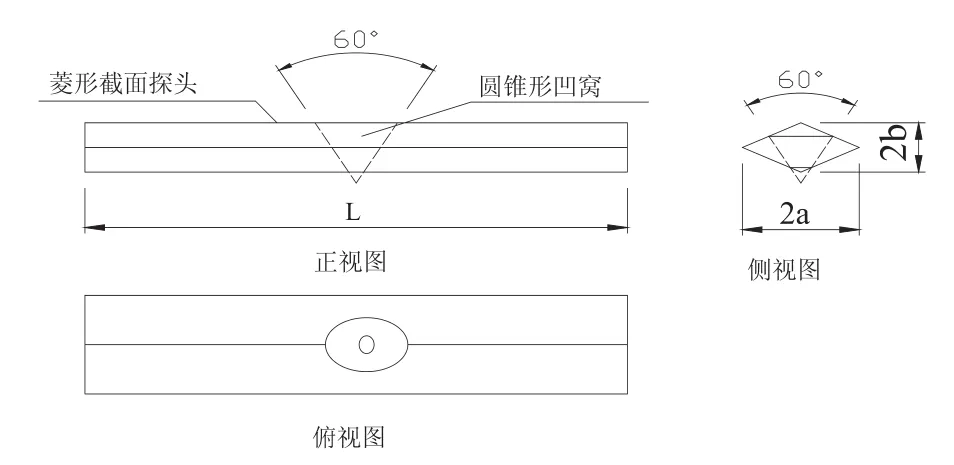
图7 锥槽式探头
见图8,丝扣式在菱形截面探头侧面中部设置与静力触探机探头端部相连接的螺丝扣。摘下双桥静力触探探头顶帽,将此螺丝扣与静力触探探头端部相连。
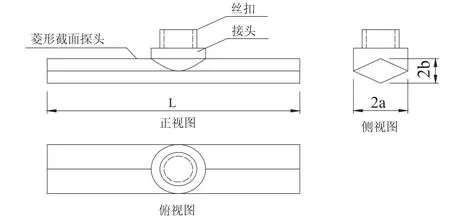
图8 丝扣式探头
下压过程中,通过探头压力传感器测读探头锥尖阻力值。该值为菱形截面探头所受地基土阻力除以静力触探探头顶帽横截面积后的数值,单位为MPa。因此将锥尖阻力乘以该面积,即得菱形截面探头在下压过程中所受阻力P。
探头阻力P与探头长度L、菱形截面探头轴长a和b、软黏土地基不排水抗剪强度有关,见式(20)。
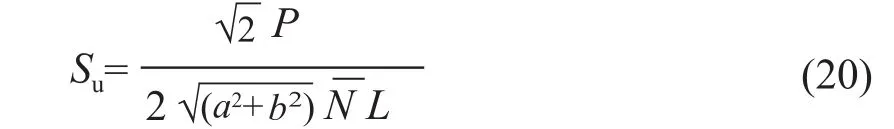
式中:N为阻力系数,与轴长比b/a有关,实际工作中取光滑与粗糙条件下的平均值进行计算。当轴长比b/a取0.5时,N-=13.28。根据式(20)可得软黏土不排水抗剪强度。测试过程中,沿深度一般每10 cm测一读数,测试速度一般取1.2 m/min。
6 结论
(1)假定软黏土服从Tresca强度条件,基于极限分析原理,求得了菱形截面T型触探探头阻力系数的解析解。
(2)研究表明随着菱形截面探头轴长比的减小,探头表面粗糙度对阻力系数的影响逐渐减小。当轴长比小于0.8时,菱形截面探头受表面粗糙度的影响小于传统圆形截面探头。工程实用轴长比可取0.5。
(3)提出了锥槽式和丝扣式两种菱形截面探头与静力触探探头之间的结合方法,提出了现场测试方法。
