功率分流风电齿轮传动系统可靠性分配

黄鼐， 潘骏， 贺青川

（浙江理工大学机械与自动控制学院，杭州310018）

0 引言

国内的风电齿轮箱主要是依据相关的齿轮标准进行设计制造，缺少可靠性设计方法，难以保证兆瓦级风电齿轮箱较长的寿命要求。可靠性分配是可靠性设计的重要环节，这里主要研究风电齿轮传动系统的可靠性分配方法。

传统的分配方法有等分配法、比例分配法、AGREE分配法[1-4]，它们均用于简单系统的可靠性分配。对于复杂系统的可靠性分配问题，用传统方法难以准确进行可靠性分配。针对系统复杂性、多层次等特点，可以应用层次分析法进行可靠性分配。

层次分析法是一种定量和定性分析结合起来的系统分析方法，运用其在可靠性分配方面的研究有很多。文献[5]~[7]运用层次分析法时，是将复杂系统简化成串联系统再进行可靠性分配。本文研究的风电齿轮传动系统结构复杂，在一、二级传动中有多个行星轮，在分配得到行星轮子系统的可靠度后，需进一步分配单个行星轮的可靠度，所以只运用层次分析法难以解决该传动系统的可靠性分配问题。

1 风电齿轮传动系统的层次结构体系

这里针对功率分流型风电齿轮传动系统进行可靠性分配，其结构如图1所示，主要由准行星轮系（1、2、3组成）、差动轮系（4、5、6组成）、定轴轮系（7、8组成）组合而成，主轴功率一部分通过一级齿圈输入，另一部分通过二级行星架输入，再经高速级齿轮7、8传递到输出轴。

在风电齿轮传动系统的设计中，轴和轴承的安全系数选择较大，导致它们的可靠性比较高，一般不易出现失效，传动系统的整体可靠主要取决于各级传动齿轮，所以将主要针对各级齿轮进行可靠性分配。

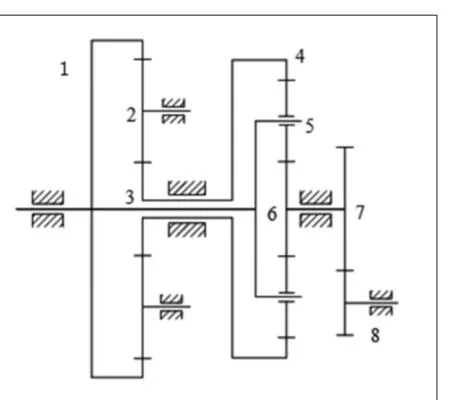
图1 功率分流风电齿轮传动系统结构简图

综合考虑以上的分析结果，以风电齿轮传动系统的整体可靠度作为目标层D，以影响系统可靠度分配的重要程度、技术水平、维修难易、成本造价4个因素作为准则层B，以传动系统中的一级齿圈、一级行星轮、一级太阳轮、二级齿圈、二级行星轮、二级太阳轮、三级主动斜齿轮、三级从动斜齿轮为对象层A，建立出层次分析的模型，按照层次分析分配方法的步骤得到满足风电齿轮传动系统整体可靠度要求的分配结果。风电齿轮传动系统的层次结构模型如图2所示。

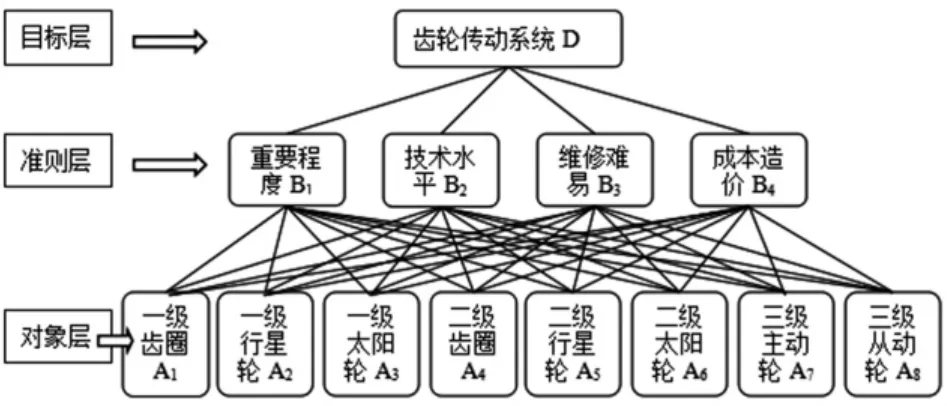
图2 风电齿轮传动系统层次分析结构模型

2 层次分析法原理

本文采用模糊层次分析方法，三标度来作为判断矩阵的标度，这就可以较容易地对因素作出相对重要的评判，并且优先判断矩阵转换成的模糊一致性矩阵满足一致性条件，所以这种方法简便、更易操作[8-10]。其具体步骤如下：

1）利用三标度法建立互补型模糊判断矩阵F，其也被叫作优先判断矩阵：

式中：甲表示第i行相对应的元素；乙表示第j列相对应的元素；n表示准则层中拥有的元素数量。

2）将上述的优先判断矩阵F转换成模糊一致性矩阵Q。先求矩阵F的行和再使用下列转换公式：

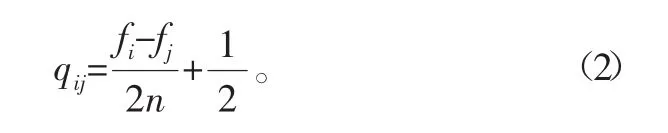
则可以求得模糊一致性判断矩阵表示如下：

3）使用行和归一的方法求出准则层的权重向量。模糊一致性判断矩阵Q的每行元素之和（其中并不包含元素自身间的比较）及矩阵Q不包含主对角线元素的总和可分别表示为：

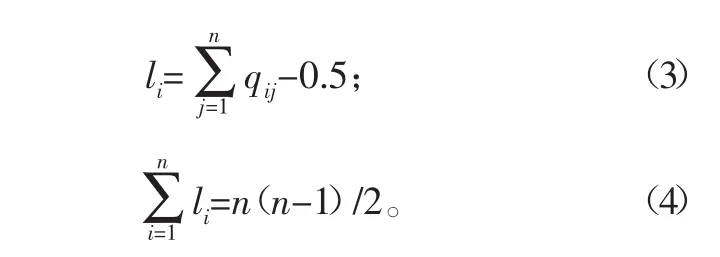
其中，li表示元素i相对于上一层元素的重要程度，所以将它进行归一化处理就可以得到准则层的各项权重指标：

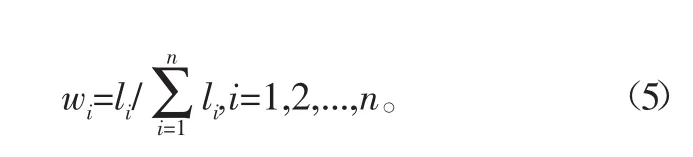
则得到准则层的权重向量表示为

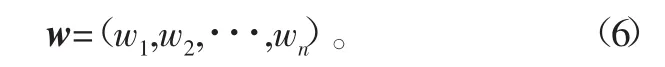
4）计算对象层的综合权重向量。重复利用上述3项操作过程，不断求出对象层各元素在准则层每个单一元素影响下的权重向量其中m是对象层的元素数量。将对象层相对于准则层的权重向量组合成矩阵表示为式中：Ps为目标层允许的失效概率；Pi为对象层第i个元素分配得到的失效概率；Wi为对象层第i个元素的综合权重。

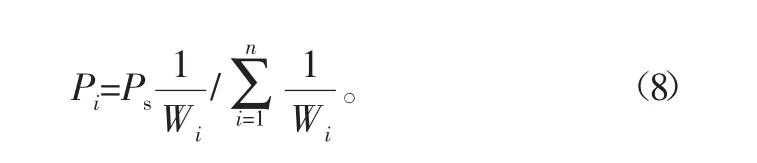
最后可以计算出对象层中第i个单元所应分配的可靠度为

3 风电齿轮传动系统可靠性分配

根据传动系统的层次结构模型和模糊三标度中的优先关系，比较准则层的每个因素对于目标层齿轮传动系统可靠性分配的影响大小。根据专家分析判断结果，整理得出影响风电齿轮传动系统可靠性因素之间的权重关系如下：重要程度＞维修难易＞技术水平＞成本造价，即B1＞B3＞B2＞B4。根据风电齿轮传动系统的具体情况及专家经验，得到对象层相对于准则层相对关系如下：

相对重要程度的关系：二级行星轮＞二级齿圈＞三级从动轮＞三级主动轮＞一级行星轮＞一级齿圈＞二级太阳轮＞一级太阳轮，即A5＞A4＞A8＞A7＞A2＞A1＞A6＞A3。

技术水平高低的关系：二级齿圈＞一级齿圈＞三级从动轮＞三级主动轮＞二级行星轮＞一级行星轮＞二级太阳轮＞一级太阳轮，即A4＞A1＞A8＞A7＞A5＞A2＞A6＞A3。

维修难易程度的关系：二级行星轮=一级行星轮＞二级齿圈=一级齿圈＞二级太阳轮＞一级太阳轮＞三级主动轮=三级从动轮，即A5=A2＞A4=A1＞A6=A3＞A7=A8。

成本造价高低的关系：二级齿圈＞一级齿圈＞三级从动轮＞三级主动轮＞二级太阳轮＞一级太阳轮＞二级行星轮＞一级行星轮，即A4＞A1＞A7＞A8＞A6＞A3＞A5＞A2。

整理分析上述关系，按照层次分析法的步骤，计算得到对象层相对于目标层的综合权重：

根据得到的综合权重向量，对风电齿轮传动系统的可靠性指标进行分配，根据相关的研究资料可知，达到20 a寿命时该齿轮传动系统的可靠度水平在0.8左右。因此当目标层可靠度指标要求为0.8时，即其失效概率P为0.2，根据层次分析法的步骤5），得到各齿轮单元应分配的可靠度为:则对象层元素相对于目标层的权重向量可以表示为

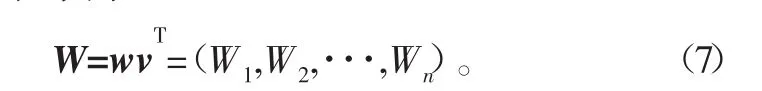
5）根据综合权重向量分配对象层的可靠性指标。根据对象层各元素的综合权重关系分配得到每个元素的允许失效概率P，再依据失效概率P就可以求得对象层各元素的可靠度。允许失效概率P与对象层每个元素的权重关系可以表示为

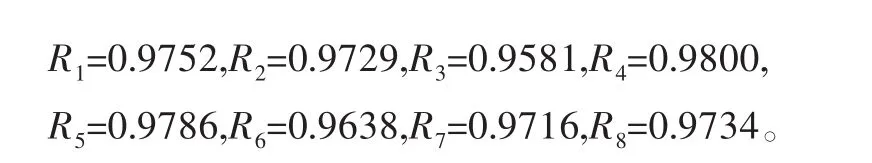
4 行星轮子系统可靠度分配

风电齿轮传动系统中行星轮的个数大于3个，特别是第一级行星齿轮传动，为了减少齿轮承受的载荷，一般都使用多个行星轮，用来提高行星传动的承载能力。在可靠度分配时，当考虑各行星轮相互独立时，单个行星轮分配的可靠度偏高，这与实际情况不相符，因此需考虑各行星轮间的相关性，可以使用Copula方法分配单元相关条件下的可靠度[11-15]。

当机械系统为串联系统时，其组成单元工作寿命间的相关性表现出来的多是正相关。设串联机械系统有n个组成单元分别记为X1，X2，…，Xn，则其失效概率为可靠度为机械系统的相关结构为CopulaCθ（u1,u2,···,un），θ为单元相关性的参数，当系统运行环境和状况不同时，单元的相关结构Cθ与相关性参数θ也会发生改变。

串联系统中任一单元的失效将导致整个系统的失效，则串联系统的可靠度可表示为

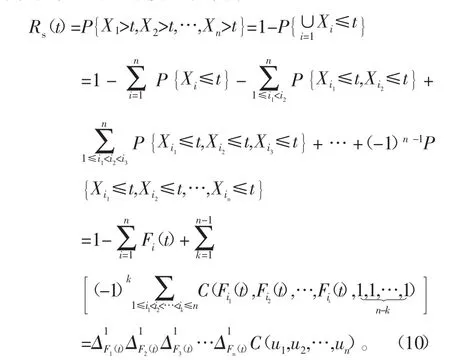
在机械串联系统中一般使用Gumbel Copula模型，即

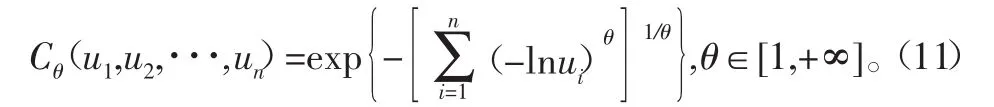
式中，θ为表示变量相关性的参数。

这里的功率分流型风电齿轮箱第一级传动中行星轮2有8个，第二级传动中行星轮5有4个，由于行星轮的参数和承受载荷均相同，故行星轮2和行星轮5中的各行星轮失效概率分别相等，分别为F2（t）和F5（t）。选取Gumbel Copula模型，考虑各行星轮间失效相关，得到如下：

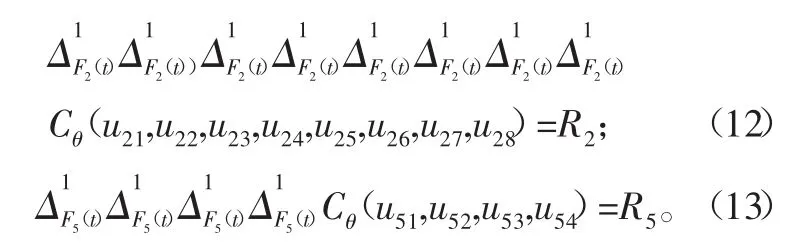
由于相关性系数θ未知，当其在0～1之间取值时，第一级和第二级传动中单个行星轮可靠度的变化如图3、图4所示。

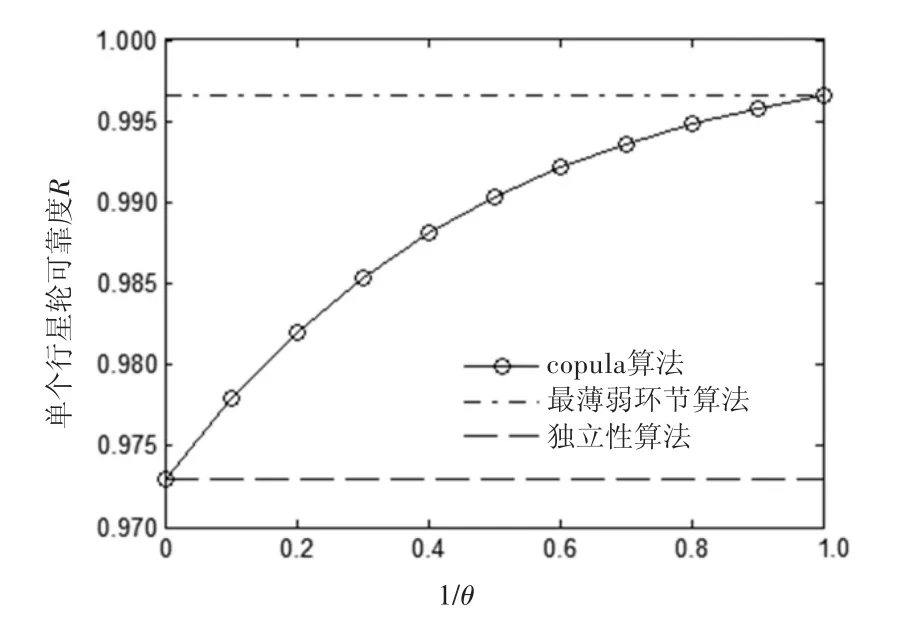
图3 第一级传动中单个行星轮分配的可靠度随相关系数的变化

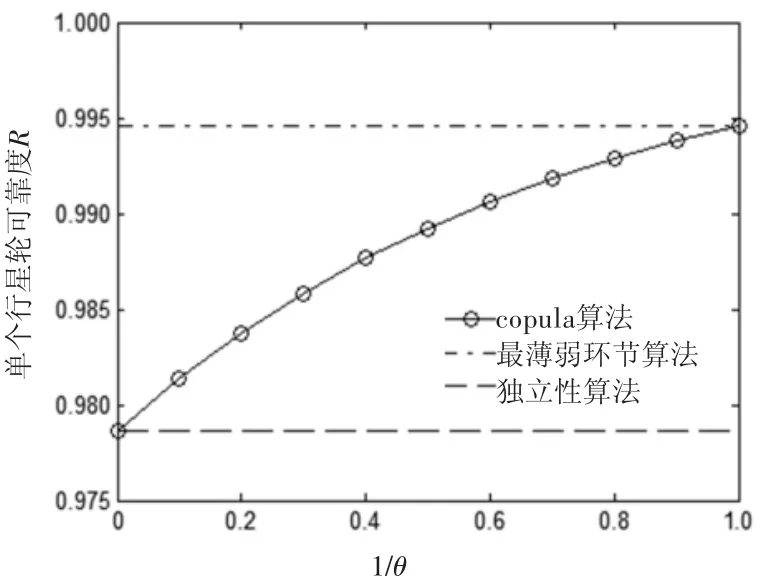
图4 第二级传动中单个行星轮分配的可靠度随相关系数的变化

由图中可知，当θ→+∞时，Copula算法与最薄弱环节算法重合，表现为单元完全相关；θ=1时，Copula算法与独立性算法重合，表现为单元完全独立。该齿轮传动系统中，行星轮间的失效呈现强相关性，对图中copula算法的曲线分析可以发现，相关系数1/θ的取值在0.2～0.4之间较为合理。

5 结 论

本文运用层次分析法理论，研究风电齿轮传动系统可靠性分配问题。主要考虑重要程度、技术水平、维修难易、成本造价4个因素的影响，对传动系统中的各齿轮进行可靠度分配，为风电齿轮传动系统的可靠性设计奠定基础。由于该功率分流齿轮传动系统第一、二级中有多个行星轮，这里考虑多个行星轮间的相关性，运用copula分配得到单个行星轮可靠度，这与工程实际更符合。