基于干曲线方程的桉树立木单株材积测算研究
2018-11-10吴志华尚秀华王睿陈鸿鹏刘果谢耀坚
吴志华,尚秀华,王睿,陈鸿鹏,刘果,谢耀坚
基于干曲线方程的桉树立木单株材积测算研究
吴志华1,尚秀华1,王睿2,陈鸿鹏1,刘果1,谢耀坚1*
(1.国家林业和草原局桉树研究开发中心,广东 湛江 524022;2.中南林业科技大学风景园林学院,湖南 长沙 410004)
以3个不同林龄的桉树品系16株样木为材料,以2种区分段所得干曲线方程,构建立木三维立体结构并对其单株材积测算方法,就所获得5种单株材积以及其形数进行了计算比较。结果表明:来自不同2种区分段所建立的干曲线方程模型拟合效果好,最大多数的模型决定系数2大于0.99,SEE(Standard Error of the Estimate)较小,能很好对样木的树干干形进行解析;但不同的区分段差别较大,其中1 m区分段所获得树干曲线方程拟合效果(2>0.98)优于1.3 m区分段;5种单株计算方法所得材积(2种区分段求积法、2种三维立体结构求积法与常规桉树二元材积法)之间没有显著差异,但存在着极显著的线性相关性;对4个林分的形数分析表明,不同林分立木在胸高形数差异显著,表现出胸高形数随着林分林龄增大而逐步减小的趋势。在胸高形数上5种单株材积测算存在着差异显著。1 m区分段下所得三维立体所得材积V4以及胸高形数均与其相应的区分求积法所得材积V2和胸高形数接近,因此可利用1m区分段建立干曲线方程获得树干三维立体结构,测算接近真实的单株材积。
桉树;区分段方法;干曲线方程;树干三维立体结构;单株材积;形数
立木材积是反映单株木体积的指标,立木材积的大小是评估森林生态变化、健康状况以及森林经营利用的最重要的指标之一[1]。在森林调查中,通常根据胸径、树高两因子对林木材积的计算,分别获得立木一元材积表和二元材积表。但编表通常需要花费大量人力、物力去收集资料,以确定材积式的参数[2],由于这些参数受到区域、树种、林龄等因素影响,因此其适用范围是有限的。在森林资源调查、评估及经营管理等上,如何高效精确地测算立木材积显得很重要。干形即树干的形状,重要的测树因子,不但影响树干材积大小和质量,而且还是某些测树用表编制的核心问题[3],其变化直接影响到林木材积及材种出材量。干形被认为是通直立木树干三要素(高、粗、形)之一,干曲线方程(又称削度方程)能很好反映树干饱满情况,是林分生长与收获预估模型体系中的重要组成部分[4],随着计算机的发展,怎样获得理想、简洁的干形表达式并用于实际仍是目标[5]。形数是树干材积与等底、同高的圆柱体体积之比,反映树干饱满程度的重要干形指标[3],同时又是与立木材积及林分蓄积量密切相关的重要因子。了解树干干形能够很好地展示树干剖面,对林木材积计算、锯材加工和出材率以及培育指导等方面具有重要的意义。
桉树()是我国南方最重要的速生、丰产的人工林树种之一[6],其木材被广泛用于制浆造纸、单板旋切和实木利用。桉树在我国发展迅速,当前人工林面积达4.5 × 106hm2,年产2.0 × 107m3木材,为我国木材生产做出了重要贡献[7]。有关桉树材积表的研究已见报道,如岑巨延[8]建立了广西桉树立木材积模型;施恭明等[9]应用交叉建模检验技术,筛选建立福建省桉树人工林二元材积方程;甘世书等[10]分别采用分段建模的方法建立海南省桉树立木材积模型;冯强等[11]以山本材积式作为基本模型,对可变参数的动态模型进行了模型建立。这些桉树材积模型均为拟合二元材积方程且研究文献不多,特别是立木材积无损精测与建模方法研究很少,这不利于桉树产业发展的需求。为此,本研究提出以3个不同林龄的桉树品系16株样木为材料,以2种区分段所得干曲线方程,构建立木三维立体结构并对其单株材积测算方法,就所获得5种单株材积以及其形数进行了计算比较,旨在建立准确、方便、快速的单株材积方法,为以后桉树人工林的生产、经营和管理等提供技术支撑。
1 研究材料及方法
1.1 试验林概况
试验林位于广东省湛江市遂溪县岭北镇南方国家级林木种苗示范基地内(N 21°30',E 111°38')。造林初植造林密度均为1 667 株·hm-2,林分保存率在85%以上。
1.2 采样方法
每个测定林分建立10 m × 10 m样地,对不同林龄树种桉树人工林林木进行每木检尺后,测定林分立木树高H、胸径DBH等生长性状,根据调查的林木选取代表整个林分平均水平且生长正常的 4 株样木作为解析木。确定南北方向,将解析木伐倒。
1.3 样木处理
解析木伐倒后,用皮尺量测树高,用直径卷尺测量胸径及伐根直径,将解析木树干从地面按照1 m分段测量树干周径,并按照1.3 m区分段对不同的木段大小头进行两个垂直方向的周径测量,以用于干曲线方程(削度方程)建立以及单株材积计算。
1.4 材积计算公式
1.4.1 桉树二元材积计算
以速生桉单株材积公式计算[11]单株材积(V1),具体计算公式:
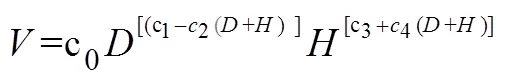
式中:为单株材积;为胸径;为树高;c=1.091 54×10-4,c=1.878 92,c=5.691 86×10-3,c=0. 652 598,c=7. 847 54×10-3。
1.4.2 桉树区分求积法的材积计算
分别对采用1 m区分段和1.3 m区分段所得的木段采用区分求积法(sectional measurement method)计算材积,即让各区分段的干形更接近于正几何体,以平均断面近似求积方法测算各分段材积和,再加上看作圆锥体的梢头部分体积,即得到全树干材积。以区分求积法得到1 m区分段所得单株材积为V2,以1.3 m区分段的所得单株材积为V3。计算方式为:
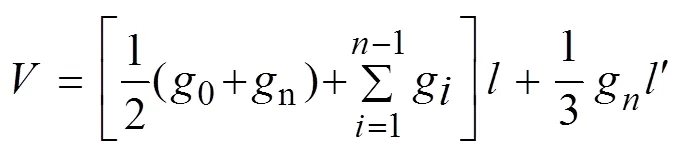
式中:g为树干底断面积:n为梢头底断面积;g为各区分段之间的断面积,、分别为区分段长度及梢头木长度。
1.4.3 基于桉树三维立体结构的材积计算
分别采用1 m区分段,1.3 m区分段建立每样木立木干曲线方程=(),干曲线方程即建立树干断面半径与树高关系,分别采用200个各种非线性拟合方程进行最小二乘法拟合分析,选择模型决定系数2大于0.90,SEE(Standard Error of the Estimate)非常小且模型显著且简洁的函数。
根据立木树干横断面形状看作为圆形,树干是干曲线围绕干轴(假设过树干中心有一条纵轴线)所形成的三维立体结构。因此树干所形成三维立体结构的材积为:
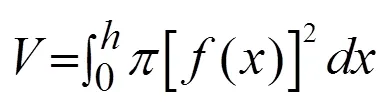
式中:()为干曲线方程,为树高。
1.5 胸高形数计算
桉树胸高形数(f1.3)按照如下公式计算:
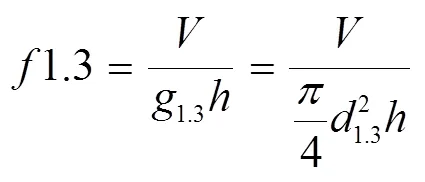
式中:为立木的单株材积,1.3为胸高形数:1.3为胸高直径:为树高。
1.6 数据处理
使用Excel 2007软件对树高、胸径、单株材积进行计算,并依据各种材积方法计算其胸高形数。使用Datafit 9.0 软件对解析木的树高、胸径进行非线性等拟合回归分析,获得干曲线模型,干曲线模型参数,方程参数统一保留4位小数。不同方法计算的材积统一保留1位小数。以SPSS 17.0 对4种不同林分的5种获得的材积以及相应的胸高形数以及实验形数进行双因子建模和效应等分析。
2 结果分析
2.1 样木的生长情况
由表1可知。树高最大值19.1 m,最小值9.2 m,平均值12.7 m,胸径分布7.2 ~ 14.0 cm,以实测的胸径平均计算,样木的平均胸径为10.5 cm。除尾巨桉林分生长高于同林龄的赤桉外,各树种树高和胸径大小均随林分林龄增加而增加。
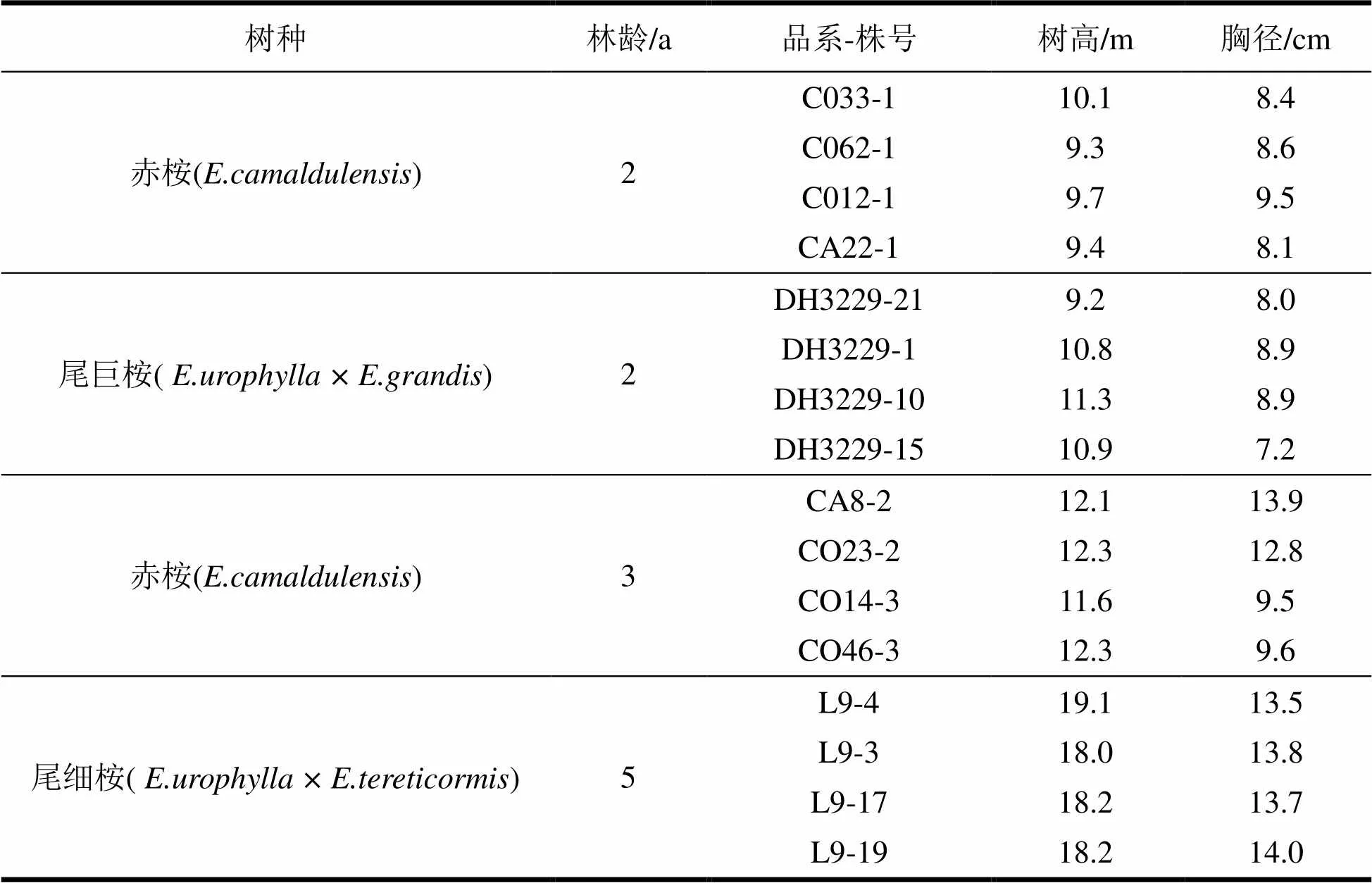
表1 4个不同林分的生长情况
2.2 不同区分段解析木的干曲线方程
分别采用1 m和1.3m区分段建立每样木立木干曲线方程=及其参数。由表2可知,所建模型均非常显著,最大多数的模型决定系数2大于0.99,最大值仅为0.595 2,表明模型拟合效果好,标准误非常小。分别比较两种区分段,发现1 m区分段所获得树干曲线方程只需=2+0.5和=3+0.5两种函数即可,且拟合效果好,决定系数均在0.98以上,而1.3 m区分段除了主要使用=3+0.5函数,还需要=a2.5+c0.5与=+2.5+c函数,且总体拟合效果略差。在不同林分样木间,仅从决定系数大小来看,差异不大。总体而言两种区分段所获得的干曲线模型可靠,能很好对样木的树干干形进行解析。
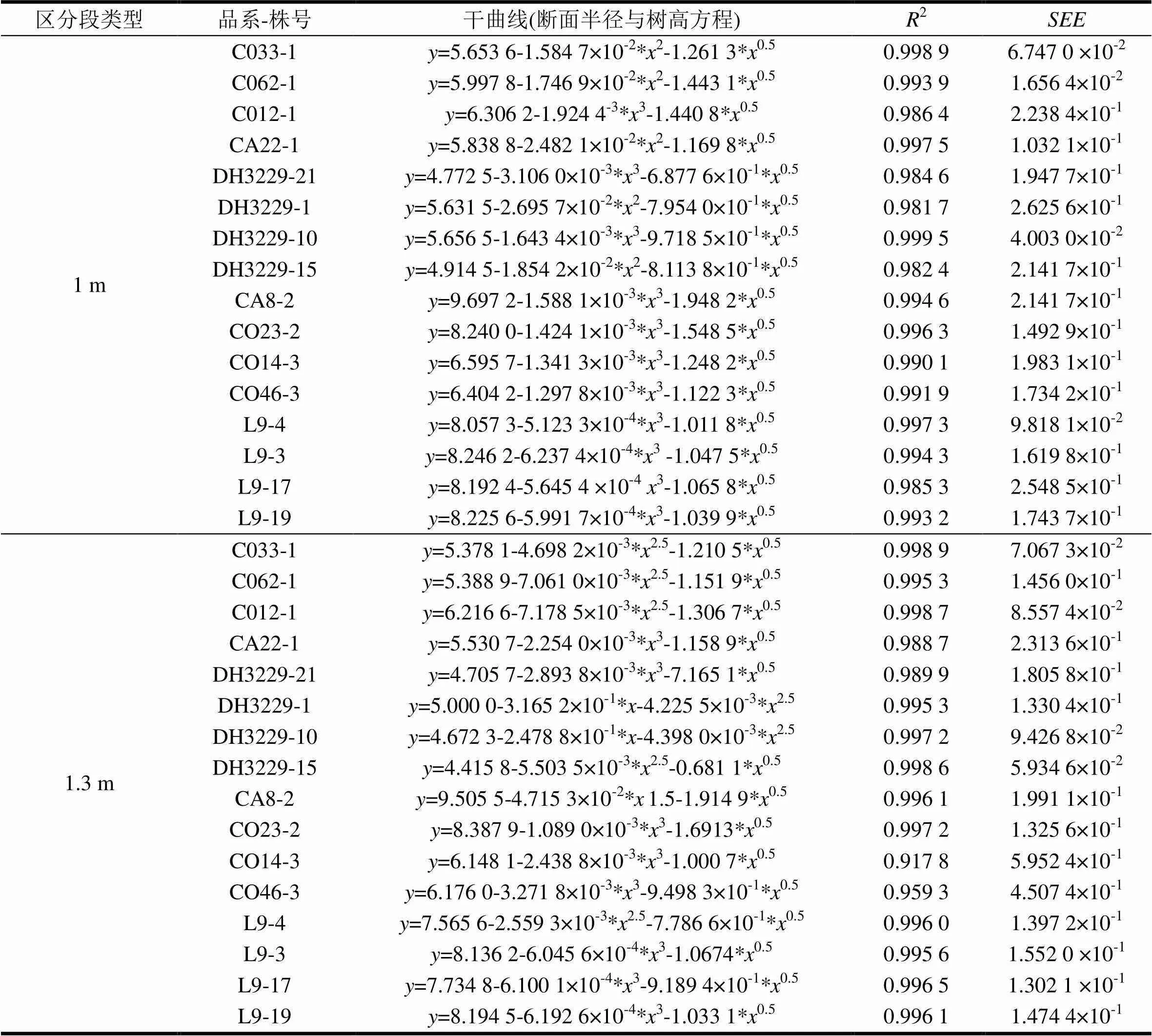
表2 不同区分段所得的各立木的干曲线方程及其参数
注:表中干曲线方程中为树干断面半径,为树干底面到计算断面。
2.3 基于2种区分段所得干曲线方程的材积计算
分别采用1 m与1.3m区分段建立每样木立木干曲线方程=,发现模型效果非常好。图1和图2为尾细桉L9-4在1 m与1.3 m区分段所得的断面半径散点图及其干曲线拟合方程。干曲线自基部向梢端的变化大致可归纳为:凹曲线(0 ~ 5m)、平行于x轴的直线(5 ~ 10 m)、类似于抛物线(>12 m)曲线类型。1 m与1.3 m区分段拟合曲线在基部部分存在着差异,其他差异不明显,因此所得到三维立体结构几乎一致(图2)。因此在此基础上可以建立相应的三维立体结构,并对其材积计算。分别根据不同单株材积方法分别获得测试立木不同的材积(表3)。
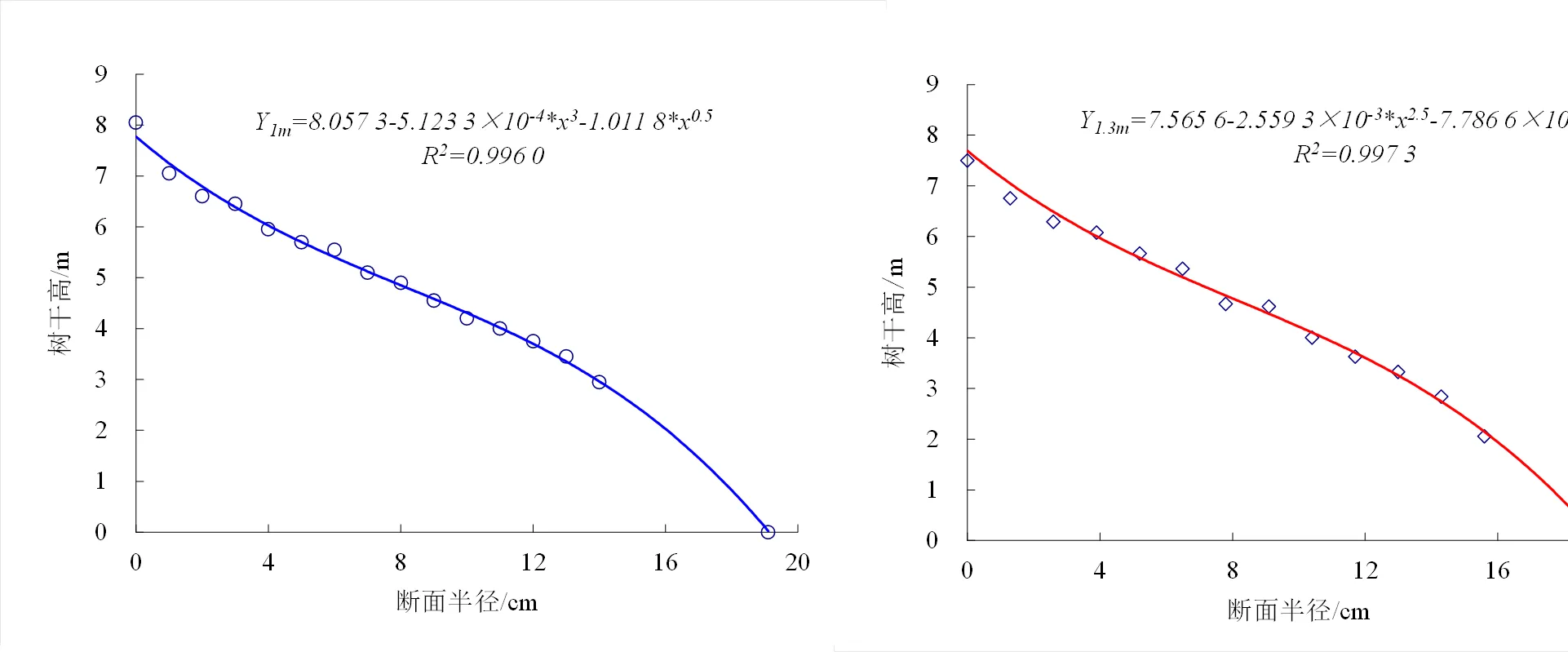
图1 1 m和1.3 m区分段所得的立木L9-4的断面半径以及干曲线拟合线
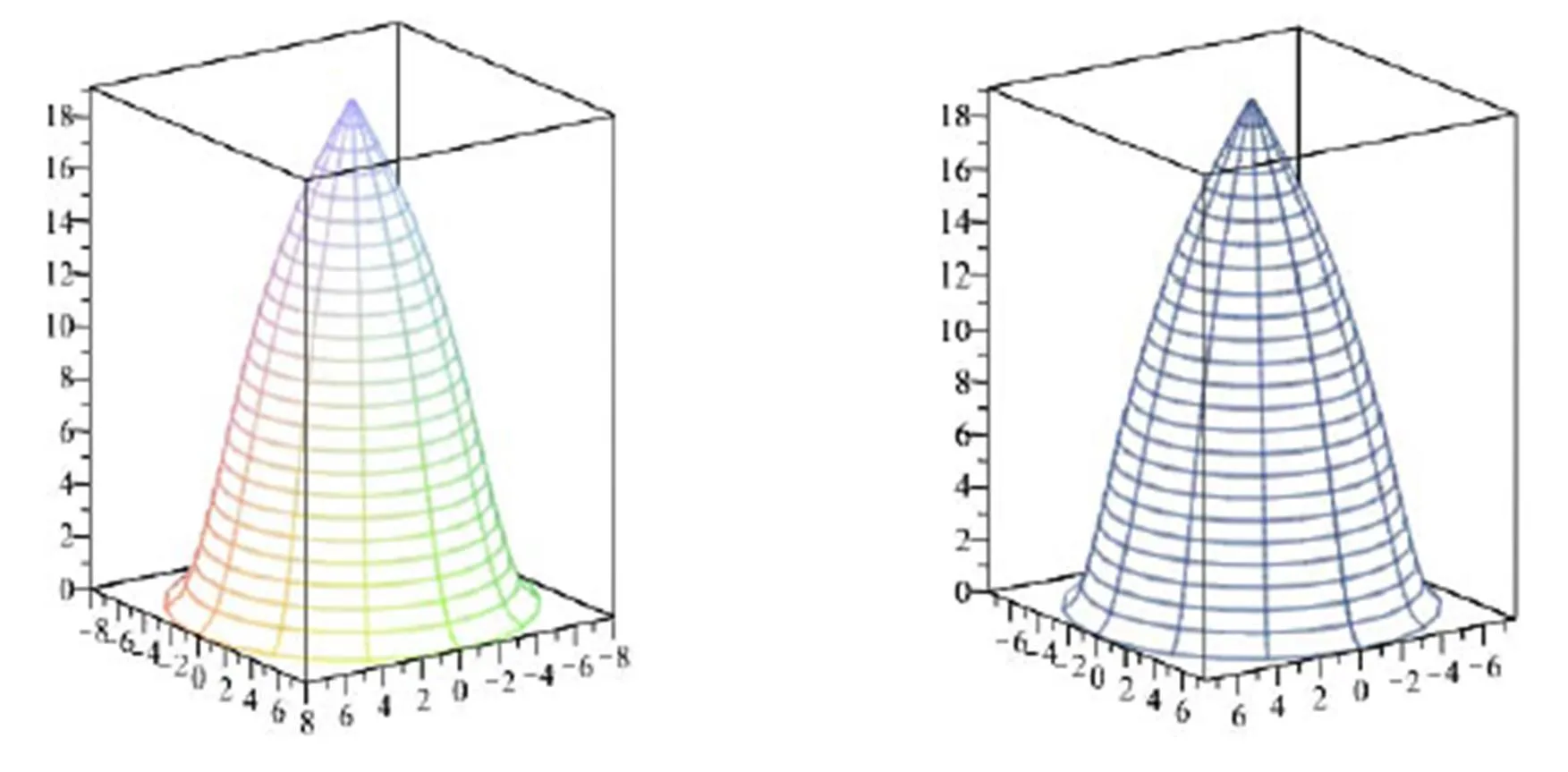
图2 立木L9-4在不同区分段所得的三维立体结构图
注:1 m区分段(左)、1.3 m区分段(右),底面坐标为断面半径(cm)而纵坐标为树高(m)。
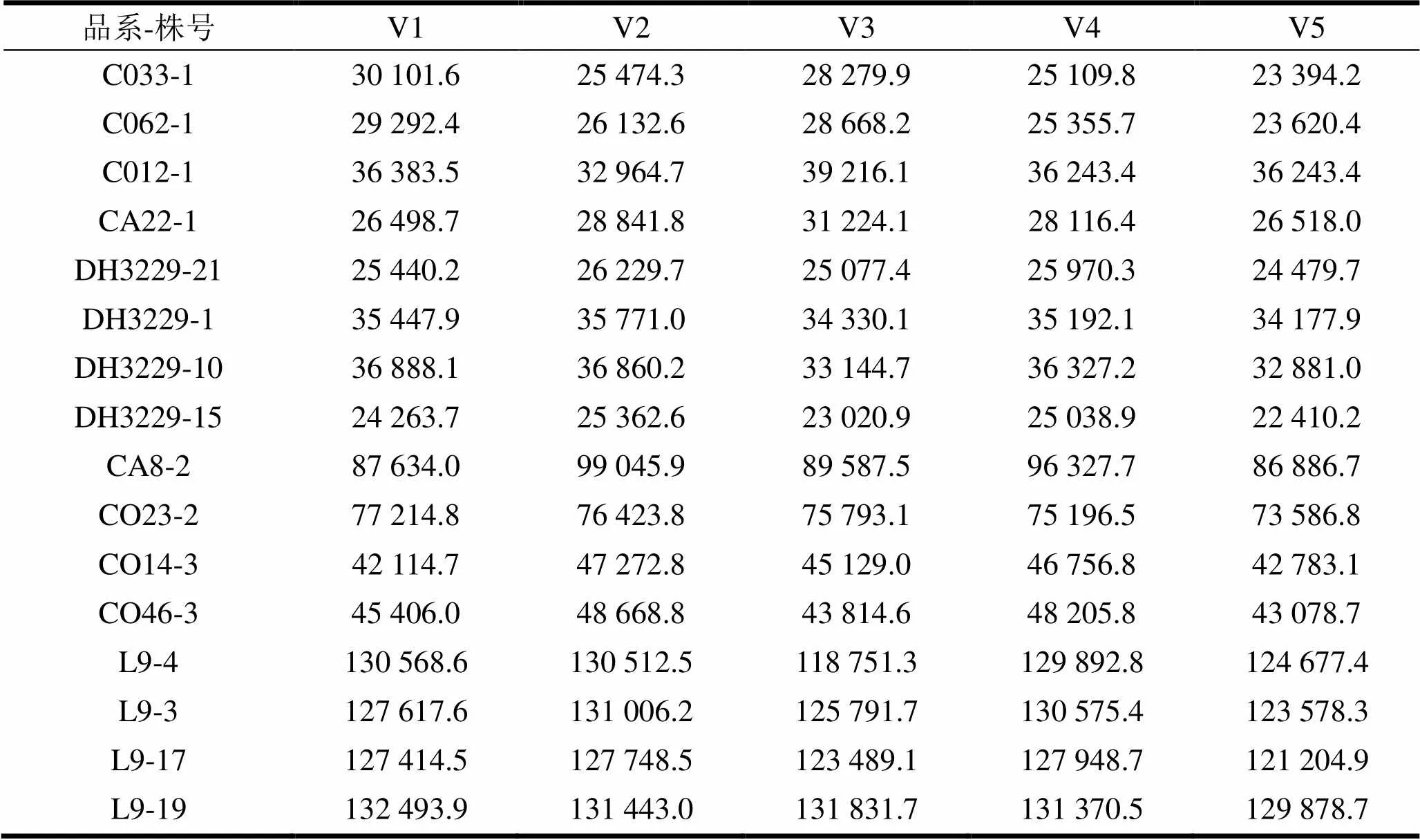
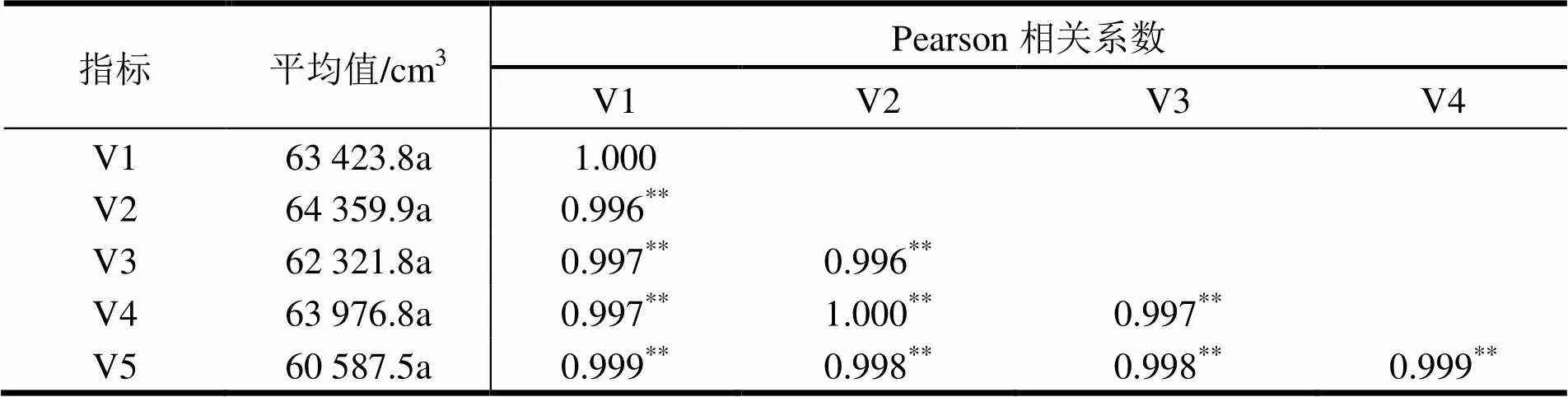
表3中V1为桉树二元材积公式计算结果,V2、V3分别为1 m、1.3 m区分求积法所得材积,V4、V5分别为1 m、1.3 m区分段的干曲线所得的三维立体结构所计算的材积。从5种材积比较来说,在不同样木之间不存在着一致性的规律,由于来源不同林分的样木之间差异很大,加之同一林龄的立木之间差异,因此对其5种材积之间的差异进行方差分析,发现不显著(表4)。另外5种材积之间存在着显著共线性关系,即各材积之间的Pearson相关系数均为大于0.99,且极显著(<0.01),特别是V2和V4两者的平均值相差不大,其相关系数为1,相关性极高,很难以对其差异区分。因此就各方法所获材积计算立木的f1.3以进一步比较。
2.4 5种材积所得的胸高形数f1.3比较
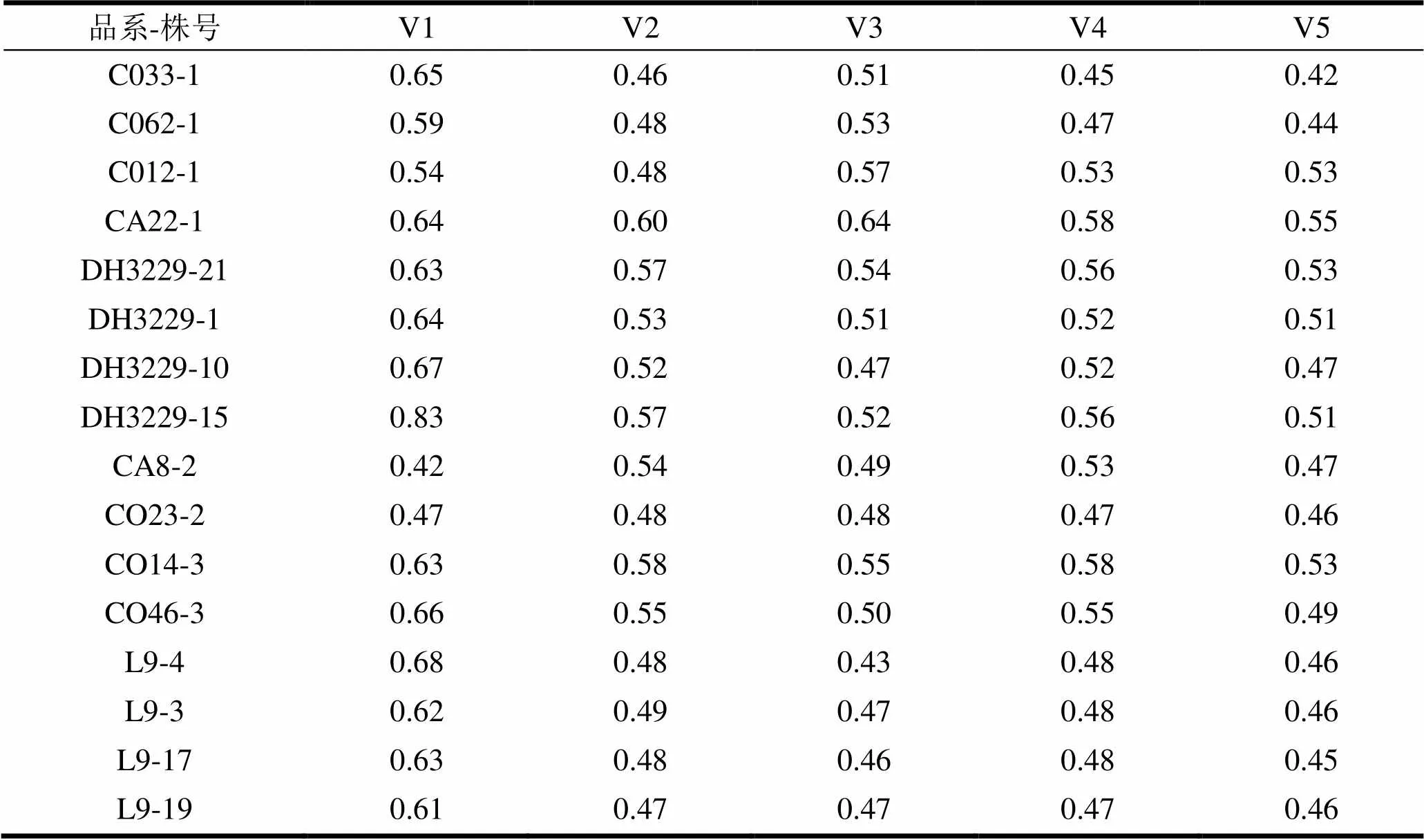
由表5可知,由桉树二元材积方程所得到胸高形数f1.3其变异范围为0.42 ~ 0.83,平均值为0.62。由1 m、1.3 m区分段的区分求积法计算的f1.3,变异范围明显要窄些,变异范围分别为0.46 ~ 0.60和0.43 ~ 0.64,f1.3平均值分别为0.52和0.51;而由1 m、1.3 m区分段的干曲线所得的三维立体的材积V4、V5所测算的f1.3明显稍低,V4所得的f1.3分别为0.51,且变异范围0.45 ~ 0.58,V5所得的f1.3为0.48,变异范围0.42 ~ 0.55,不同林分立木之间变异趋向减小。
表3 几种计算方法所获得立木材积 cm3
品系-株号V1V2V3V4V5 C033-130 101.625 474.328 279.925 109.823 394.2 C062-129 292.426 132.628 668.225 355.723 620.4 C012-136 383.532 964.739 216.136 243.436 243.4 CA22-126 498.728 841.831 224.128 116.426 518.0 DH3229-2125 440.226 229.725 077.425 970.324 479.7 DH3229-135 447.935 771.034 330.135 192.134 177.9 DH3229-1036 888.136 860.233 144.736 327.232 881.0 DH3229-1524 263.725 362.623 020.925 038.922 410.2 CA8-287 634.099 045.989 587.596 327.786 886.7 CO23-277 214.876 423.875 793.175 196.573 586.8 CO14-342 114.747 272.845 129.046 756.842 783.1 CO46-345 406.048 668.843 814.648 205.843 078.7 L9-4130 568.6130 512.5118 751.3129 892.8124 677.4 L9-3127 617.6131 006.2125 791.7130 575.4123 578.3 L9-17127 414.5127 748.5123 489.1127 948.7121 204.9 L9-19132 493.9131 443.0131 831.7131 370.5129 878.7
表4 几种计算方法所获得立木材积平均值以及其相关系数
指标平均值/cm3Pearson相关系数 V1V2V3V4 V163 423.8a1.000 V264 359.9a0.996** V362 321.8a0.997**0.996** V463 976.8a0.997**1.000**0.997** V560 587.5a0.999**0.998**0.998**0.999**
注:表中不同数字后小写字母表示在0.05水平上差异显著,数字后**表示在0.01水平上相关性显著。
表5 几种计算方法所获得立木胸高形数
品系-株号V1V2V3V4V5 C033-10.650.460.510.450.42 C062-10.590.480.530.470.44 C012-10.540.480.570.530.53 CA22-10.640.600.640.580.55 DH3229-210.630.570.540.560.53 DH3229-10.640.530.510.520.51 DH3229-100.670.520.470.520.47 DH3229-150.830.570.520.560.51 CA8-20.420.540.490.530.47 CO23-20.470.480.480.470.46 CO14-30.630.580.550.580.53 CO46-30.660.550.500.550.49 L9-40.680.480.430.480.46 L9-30.620.490.470.480.46 L9-170.630.480.460.480.45 L9-190.610.470.470.470.46
进一步比较不同来源的立木以及5种材积测定所得形数之间的差异,分别建立材积测定方法(因子A)、立木林分类型(因子B)两因子因子模型。由表6可知,所建立的因子模型显著,f1.3的值小于0.001。从形数看,不同因子对f1.3的影响均显著,不同材积测定方法所获得f1.3估测存在着显著的差异。即立木林分类型(B)之间的差异,表明不同的树种和林龄对立木的干形影响显著,且两因子之间存在着显著的交互作用,即不同的测定方法对不同林龄树种的材积估算差异影响较大。
表6 f1.3因子模型统计表

项目平方和自由度均方F值P值 模型0.268 9190.014 25.670 2< 0.000 1 A0.035 940.009 03.600 70.010 7 B0.141 630.047 218.905 1< 0.000 1 A × B0.091 4120.007 63.051 30.002 1
分别就两种因子影响下模型所得立木形数进行重新比较,发现V1和V4中f1.3随着林分林龄增大而逐步减小,而V2、V3和V5中f1.3虽有高有低,但总的趋势也是如此。1 m区分段在区分求积法与三维立体空间所得计算的材积更为接近,因此1 m区分段相对于1.3 m区分段,更能反映树干特性,材积更接近真实材积。2 a生的赤桉V4所得的f1.3,相比同林龄的尾巨桉V4所得的f1.3明显要高些,由于尾巨桉无性系比较均匀,干形明显优于来源于不同家系的赤桉,f1.3大小可能与树种特性有关。赤桉不同林龄比较,除了V5稍增加外,V1-V4均表现出随林龄增大而f1.3减小的变化规律,特别是5 a生尾细桉f1.3,明显的低于其他林分,进一步说明f1.3随着林龄增加呈降低的趋势。
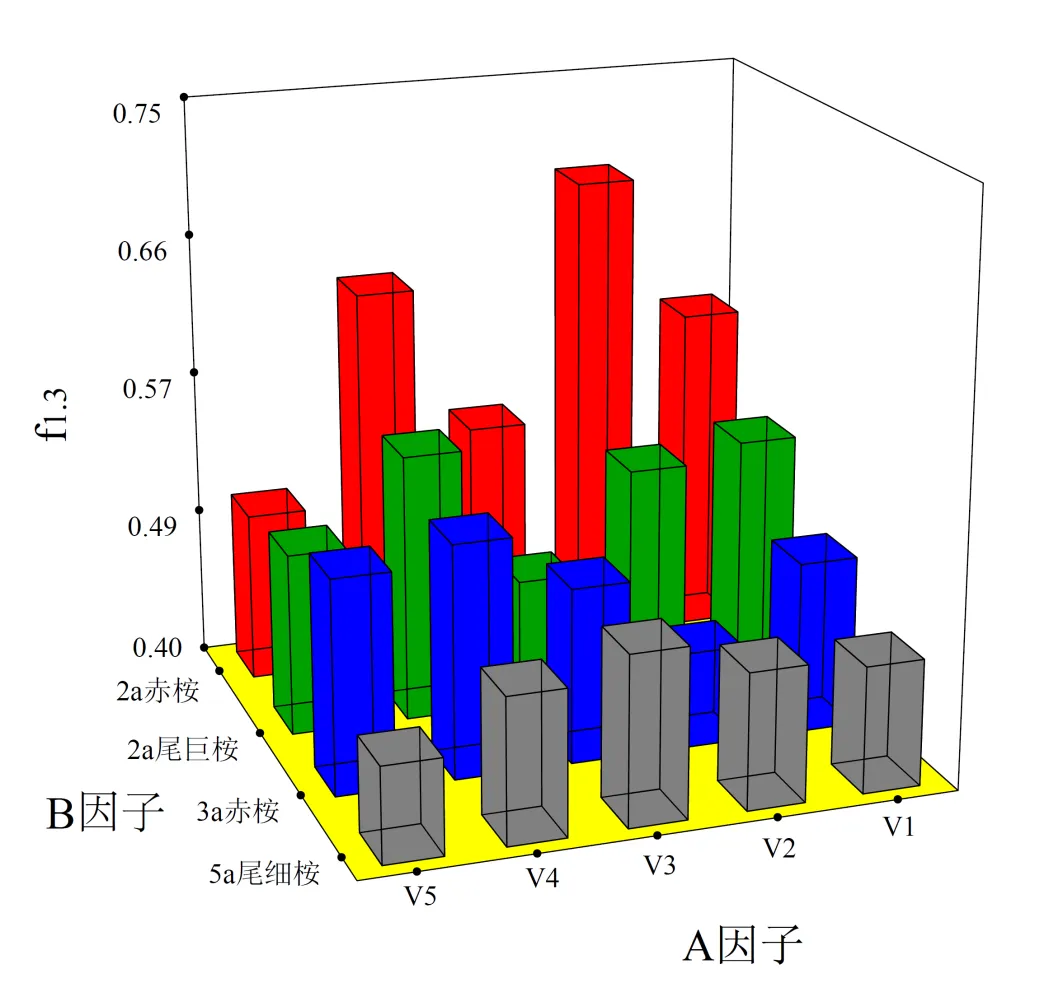
图3 不同因子影响下胸高形数的模型值
3 小结与讨论
按照干曲线发展阶段,以大致分为三类:1)简单干曲线方程;2)分段干曲线方程;3)可变参数干曲线方程。简单曲线方程的优点是容易拟合,预测精度较好[1]。由于把树干的不同部位可以近似地看作不同的几何体,简单曲线方程不一定能满足要求,因此,还要采取分段干曲线方程以及可变指数干曲线动态模型以描述树干的形状,其模拟精度较高,但是也较为复杂,在这复杂的模型结构中就存在一些不确定性[1]。
桉树相对其他树种来说,干形较好,因此本研究中采用简单的干曲线方程拟合发现效果较好,但不同的区分段差别较大,其中1 m区分段所获得树干曲线方程主要为=2+0.5和=3+0.5,且拟合效果好(2>0.98),而1.3 m区分段除了使用=3+0.5函数外,还需要=+2.5+0.5,=2.5+函数,且个别立木拟合效果略差,相比而言,1 m区分段比1.3 m区分段更优于获得树干形态。
5种计算方法所得材积之间没有显著差异,但存在着极显著的线性相关性,以 1 m 区分材积、1.3m区分材积近似立木实际材积,由其干曲线所建立三维立地材积与传统的区分求积所得材积基本接近,无明显差异,而1 m区分段所得三维立体材积与区分材积差异更小。
对4个林分的形数分析表明,不同林分立木在胸高形数差异显著,表明林木干形受树种、林龄以及立地环境等多重因素影响,表现出胸高形数随着林分林龄及林木的生长变大而逐步减小的趋势,这与已有的报道[12]是一致的。5种单株材积测算发现所得胸高形数差异显著。1 m区分段所得三维立体所得材积V4与相应的区分求积法所得材积V2以及胸高形数也接近,因此可利用1 m区分段建立干曲线方程获得树干三维立体结构,测算接近真实的单株材积。
[1] 杜婧,冯仲科,樊潇飞,等.基于1stOpt软件的二元立木材积方程的研究[J].中南林业科技大学学报,2014,34(4):64-67.
[2] 王铁牛,郑小贤,田格日勒.针叶树理论材积式的适用性研究[J].华北农学报,2004(S1):50-55.
[3] 孟宪法,李悦黎,白林波.树干形状应用研究进展[J].陕西林业科技,2000(3):60-65.
[4] 段爱国,张建国.树木干形模拟技术探讨[J].林业资源管理,2013(4):37-41.
[5] 曲佳,张雄清.国内外树干干形的研究进展[J].林业科技通讯,2015(7):3-7.
[6] LUO J Z, ARNOLD R J, LU W H, et al.Genetic variation inandfor early growth and susceptibility to the gall waspin China[J].Euphytica,2014,196(3):397-411.
[7] 谢耀坚.真实的桉树[M].北京:中国林业出版社,2015.
[8] 岑巨延.广西桉树人工林二元立木材积动态模型研究[J]. 华南农业大学学报,2007(1): 91-95.
[9] 施恭明,洪端芳,严思钟,等.福建省桉树二元立木材积表研制[J].林业勘察设计,2013(2):6-12.
[10] 甘世书,贺鹏,肖前辉,等.利用分段建模方法建立海南省主要树种立木材积模型[J].中南林业科技大学学报,2018,38(5):18-22.
[11] 冯强,方良.海南桉树立木材积模型研建[J].中南林业调查规划,2014,33(3):47-51.
[12] 钟德军,李淑阁,杨景辉,等.落叶松树干干形的研究[J].河北林果研究,2004(2):126-129.
Volume Assessment of Standing Eucalypt Trees Based on Stem Curve Equations
WU Zhihua1, SHANG Xiuhua1, WANG Rui2, CHEN Hongpeng1, LIU Guo1, XIE Yaojian1
(1.,,,; 2.)
Sixteen sample trees of various ages representing threespecies were used to develop standing tree stem taper equations, and then to calculate individual tree volumes and form factors by two sectional methods. The stem curve equations established from the two sectional methods proved to fit well with, the coefficients of determination being over 0.99, and their SEEs(Standard Error of the Estimate) were small indicating the stem form of the sampled trees to be well defined by the stem curve equations developed. However, the fit of the stem curve equations differed between the two different sectional methods, with the equation from the 1 m sectional method having higher coefficients of determination than did the 1.3 m sectional method. There were no significant differences among the 5 kinds of individual volume estimates, which included two methods of sectional measurements, three-dimensional structure volume estimation using two sectional methods, and a conventional method based on a binary standing volume equation. However, significant differences were found among the form factors of four stands, and the form factor values gradually decreased as stand age increased. There were also significant differences in the form factors among 5 kinds of individual volume estimates; V4 estimates obtained from the 1 m sectional method were close to V2 estimates. It was concluded that the three-dimensional stem structure could be ascertained best using a stem taper equation obtained using the 1 m sectional method, and individual tree volumes estimated using this equation were close to actual individual tree volumes.
; sectional method; stem curve equation; three dimensional structure of stem; individual tree volume; form factor
S758.5
A
国家重点研发计划(2017YPD0601202);国家自然科学基金项目(31570615)。
吴志华(1974— ),男,在读博士,副研究员,主要从事林木逆境生理研究,E-mail:wzhua2889@ 163.com.
谢耀坚(1961— ),博士,研究员,主要从事森林培育与林木遗传育种,E-mail:cercxieyj@163.com
