基于等高线的地形特征提取算法研究

任振娜

（武警指挥学院，天津 300250）

[关键字] 等高线数据；Delaunay三角网；地形特征；提取

1 引言

地形特征是指对于描述地形形态有着特别意义的地形表面上的点、线、面，它构成了地形变化起伏的骨架。其中，地形特征点包括：山峰点、谷底点、鞍部点等，地形特征线包括：山脊线、山谷线等。地形特征是地形地表在空间分布、延展的具有骨架化控制作用的重要结构化信息，在地图制图、地貌形态识别、水文分析等领域具有重要的支持作用。由于历史的原因，现有的地形数据更多的是等高线，DEM建立的数据来源也主要是等高线，这样如何基于等高线建立DEM模型，如何基于建立的模型提取地形结构特征便成为一个感兴趣的问题。

总体思路：首先利用等高线数据构建不规则三角网DEM模型，然后通过对三角网进行分析，提取地形结构特征[1]。而本文是在基于等高线一次性构建Delaunay三角网模型的基础上，进一步分析了模型的特点，研究了山脊线和山谷线的提取算法。

2 基于等高线一次性构建Delaunay三角网模型算法描述

2.1 算法中用到的概念

定义1：约束边，本文中称由等高线上的相邻两点确定的线段为约束边。

定义2：约束边的起始点和终止点，设约束边是由等高线上相邻两个点M，N逆时针相连而成，则称M点是约束边的起始点，N点是约束边的终止点。

定义3：基边，以某一边为基准边，在点集中选取第三点与其构成一个三角形，该边就称为基边。

定义4：左右三角形，以约束边的起始点→终止点的方向为基准方向，约束边与位于基准方向右侧的点组成的三角形称为右三角形，该点称为该条约束边的右侧第三点，约束边与位于基准方向左侧的点组成的三角形称为左三角形，该点称为该条约束边的左侧第三点。

定义5：平三角形，是指三角形的三个顶点都在同一条等高线上。

2.2 基于等高线构建Delaunay三角网算法[2]

算法的具体过程描述如下：

步骤1：将每一段等高线上的点数据以其X，Y坐标，进行逆时针排列，相邻两点构成一条约束边。记录点数据到点数据链表,记录约束边数据到边链表中，并将每一条等高线数据作为一个子元素记录到等高线数据链表。

步骤2：根据点数据链表创建点数据格网索引。

步骤3：置标志位于边链表的表尾。

步骤4：在等高线链表中，依次将每一个子元素中的每一条约束边作为基边，应用夹角最大准则生成左右三角形。更新点数据信息，记录新生成的边到边链表，记录新生成的三角形到三角形链表，更新基边信息。

步骤5：从标志位的下一条边开始(即第一条非约束线段)，依次取出边作为基边，向左应用夹角最大准则生成新的三角网，更新点数据信息，记录新生成的边到边链表，记录三角形信息，更新基边信息。

步骤6：从标志位的下一条边开始，依次对同时存在左右三角形的非约束边，判断该边与其左右侧第三点组成的边是否相交，如果相交，则应用简化的LOP优化算法对三角网进行优化处理。

3 地形特征提取算法

3.1 特征点提取算法

山脊线和山谷线上的点在等高线上的特征表现为等高线局部曲率最大点，也就是等高线弯曲变化的特征点。曲线特征点的提取算法有多种。其中Split法是一种较常用的曲线特征点提取算法。该法从原理上讲属于整体算法，它所提供的曲线特征点能够保证曲线变形在规定的限差之内。

Split法的基本思想是[3,4]：先用曲线的最左边和最右边的两个点作为起始点(对于闭合曲线)将闭合曲线分为两部分，对于非闭合曲线选择其两个端点作为起始点。起始点确定后，顺序计算曲线上位于两个起始点之间的每一个点距两个起始点连线的垂距，并找出最大垂距点。若该点处等高线张角小于给定的阈值，则该点为特征点。它将原曲线分为两部分，对每一部分确定新的起始点，即用该点分别与原两个起始点构成两对新的起始点，用相同的方法对这两段曲线找出各自的特征点。Split法的原理可用图1表示。

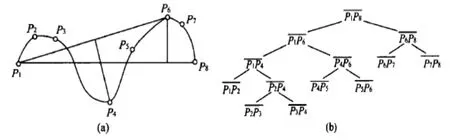
图1 Split法的原理

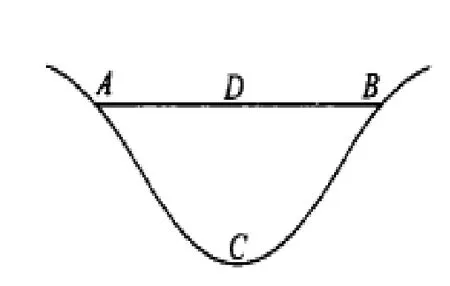
图2 识别山脊点山谷点原理图

3.2 山脊点和山谷点的识别算法

应用Split法，即可找出特征点。找出特征点后，还要对其进行分析判断，找出哪些特征点是山脊点，哪些特征点是山谷点。

最直观的判断山脊点山谷点的方法如图2所示，即计算特征点C处等高线张角范围内某点D的高程，并与C点高程比较，如果D点的高程大于C点高程，则C点为山脊点，反之，C点为山谷点。此种方法看似简单，但计算D点高程算法复杂，计算量大，影响判断效率。本文建立的Delaunay三角网模型是以等高线线段为约束边构建的，因此，模型中每一个平三角形三个点均落于一条等高线上；每一个非平三角形三个点分别位于两条等高线上。因此，在识别山脊点和山谷点时，主要步骤如下：

步骤1：从等高线链表中，依次选出第n条线段ln和第n+1条线段ln+1[5,6]，以及两条线段的三个端点dn、dn+1、dn+2。

步骤2：计算以ln为起始方向线，顺时针到ln+1的角度值。

步骤3：当角度值>195°（195°是阈值）时：根据ln找到其右三角形的第三个点，当第三个点的高程值小于dn+1的高程值，则点dn+1是山谷点，更新点信息；当第三个点的高程值大于dn+1的高程值，则点dn+1是山脊点，更新点信息；当第三个点的高程值等于dn+1的高程值，则转入步骤5。

步骤4：当角度值<165°（165°是阈值）时：根据ln找到其右三角形的第三个点，当第三个点的高程值小于dn+1的高程值，则点dn+1是山脊点，更新点信息；当第三个点的高程值大于dn+1的高程值，则点dn+1是山谷点，更新点信息；当第三个点的高程值等于dn+1的高程值，则转入步骤6。

步骤5：根据ln找到其左三角形的第三个点，如果第三个点的高程值大于dn+1的高程值，则点dn+1是山谷点，更新点信息；如果第三个点的高程值小于dn+1的高程值，则点dn+1是山脊点，更新点信息；如果第三个点的高程值等于dn+1的高程值，则转入步骤7。

步骤6：根据ln找到其左三角形的第三个点，如果第三个点的高程值大于dn+1的高程值，则点dn+1是山脊点，更新点信息；如果第三个点的高程值小于dn+1的高程值，则点dn+1是山谷点，更新点信息；如果第三个点的高程值等于dn+1的高程值，则转入步骤8。

步骤7：从ln开始，围绕dn+1依次找其右三角形，直至右三角形的某一点高程值不等于dn+1的高程值为止。当该点高程值小于dn+1的高程值，则点dn+1是山谷点，更新点信息；当该点高程值大于dn+1的高程值，则点dn+1是山脊点，更新点信息。

步骤8：从ln开始，围绕dn+1依次找其右三角形，直至右三角形的某一点高程值不等于dn+1的高程值为止。当该点高程值小于dn+1的高程值，则点dn+1是山脊点，更新点信息；当该点高程值大于dn+1的高程值，则点dn+1是山谷点，更新点信息。

3.3 山脊线和山谷线的生成

3.3.1 连接山谷线

连接山谷线是按照由高向低逐条等高线来搜索的，其搜索过程如下：

步骤1：先从高程最高的等高线起，找出没有向下连接的山谷点dn，以及与其相连接的两个点dn-1、dn+1和两条线段ln、ln+1。

步骤2：以围绕dn，搜索边ls从ln开始，向右搜索三角形的第三点d3，当d3不是山谷点时，ls=d3dn，继续向右搜索三角形的第三点，直至d3是山谷点或者ls=ln+1时为止。

步骤3：当存在山谷点d3时,将dn与d3相连接。

步骤4：重复1、2、3步，直至所有的山谷点都向下搜索不到新的山谷点为止。

3.3.2 连接山脊线

连接山脊线则是由低向高逐条等高线来搜索的，其搜索过程如下：

步骤1：先从高程最低的等高线起，找出没有向上连接的山脊点dn，以及与其相连接的两个点dn-1、dn+1和两条线段ln、ln+1。

步骤2：以围绕dn，搜索边ls从ln开始，向左搜索三角形的第三点d3，当d3不是山脊点时，ls=d3dn，继续向左搜索三角形的第三点，直至d3是山脊点或者ls=ln+1时为止。

步骤3：当存在山脊点d3时,将dn与d3相连接。

步骤4：重复1、2、3步，直至所有的山脊点都向上搜索不到新的山脊点为止。

3.3.3 说明

连接山谷线时，在某点向下找不到可以连接的山谷点的原因可能是此山谷线到达了封闭的盆地底部或谷底线流入湖泊或海洋，另一种可能是等高线在这一部分分布太稀，数字化点太少而不能足够详细地描述地貌形态；连接山脊线时，在某点向上找不到可以连接的山脊点的原因可能是此山脊线到达了山顶；在某点搜索到的山谷线(山脊线)的下一点是别的山谷线(山脊线)上的点的原因是两条山谷线(山脊线)汇合在此点。

4 实验实例

为了检验本文算法的正确性和有效性，笔者在VisualC++编程环境中对上述算法进行了实践。本实验采用的数据是某一地区的147条数字化地形等高线。图3为原始等高线数据，图4为基于等高线数据构建的局部Delaunay三角网，图5为提取的山谷线，图6为提取的山脊线。从图4-6所示的实验结果可以看出，用本文所提出的算法提取出的山脊线和山谷线是较为准确的，与实际地形也是相符合的。

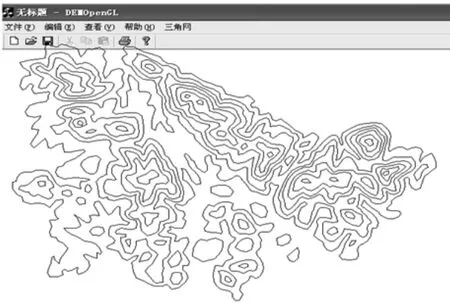
图3 等高线数据

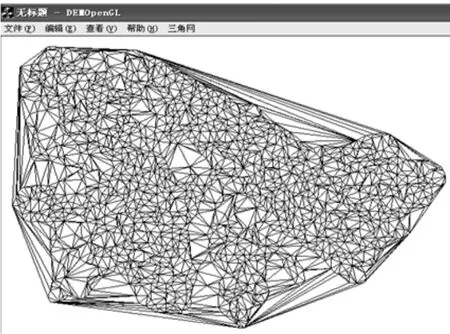
图4 Delaunay三角网模型

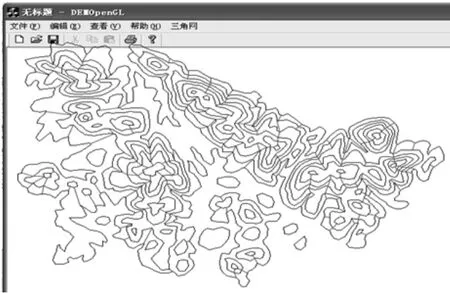
图5 提取的山谷线

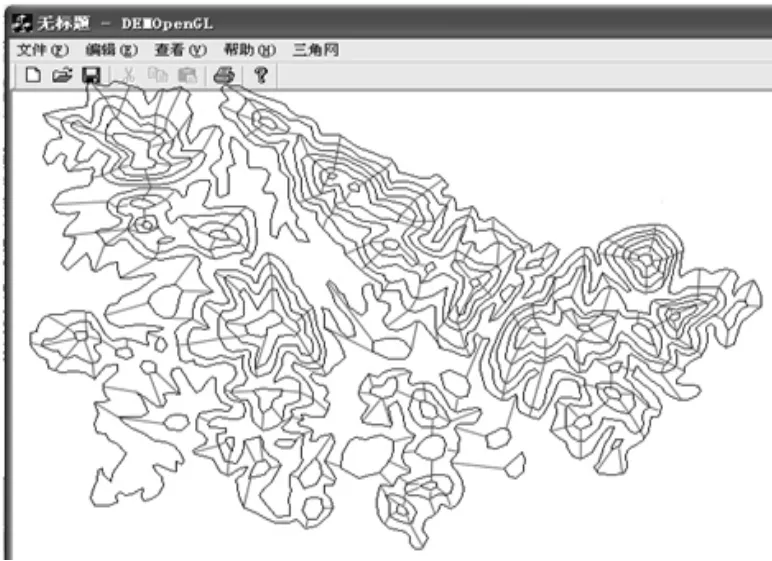
图6 提取的山脊线