基于海洋表面反射原理的多跳高频无线电传播探索

张路莹 许亚迪 刘家林 张 兴 郑文青

（山东科技大学，山东 济南 230031）

1 引言

高频(HF)的定义是从3mhz到30MHz。两个远点可以使用高频无线电波进行信号传输。当发射的信号频率小于MUF（最大可用频率）时，无线电波可以通过电离层反射回地球表面。MUF主要与电离层数有关，电离层数受季节等外部因素影响。当无线电波通过海面时，海洋湍流影响海水的电磁梯度、海洋的局部介电性和渗透性，并改变反射高度和角度。

2 模型的建立与求解

有效的漫反射区域通常是椭圆形的，由镜面反射周围的漫反射点形成。通过查阅资料可得

其中

通过查阅资料,在无穷小的有效扩散面积内，漫反射系数ρroughness和镜面反射系数ρs存在以下关系

在波涛汹涌的海面上，第一次反射后无线电波的能量损失为

初次经过平静的海面或汹涌的海面反射后能量损失的比值为

利用递归得思想可建立第一个反射和最后一个反射之间的函数关系。由于整个反射过程可以逐级分解，每个反射都只与前一个反射有关，所以我们可以利用第一个反射进行推理。由此我们可以找到相应的跳限值。

在地球表面的一点上发射的无线电波首先通过电离层。电离层的数量随季节和一天的时间而变化。当无线电波信号通过多层电离层进行折射后，入射角和反射角会产生角度差。角度差与波速和传播路径长度有关。传播路径越长，角度差越大。

信噪比(SNR)是信号总能量与噪声总能量的比值。能量损失主要是由于漫反射产生的海杂波引起的，所以这里的海杂波就是噪声。噪声的强度可以近似地用能量损失值代替。

反射角为

电离层吸收信号功率

最后一个反射递归方程为

其中

第一次完全反射后的能量值为

最后一个反射角为

根据信噪比的定义，我们知道

因此，我们可以建立反射递归模型，利用MATLAB求解递归方程，得到不同情况下的hops极限值。

平滑地形反射后的无线电波能量损失为

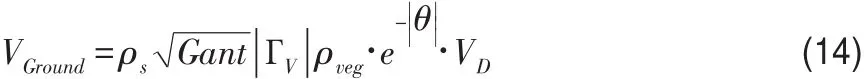
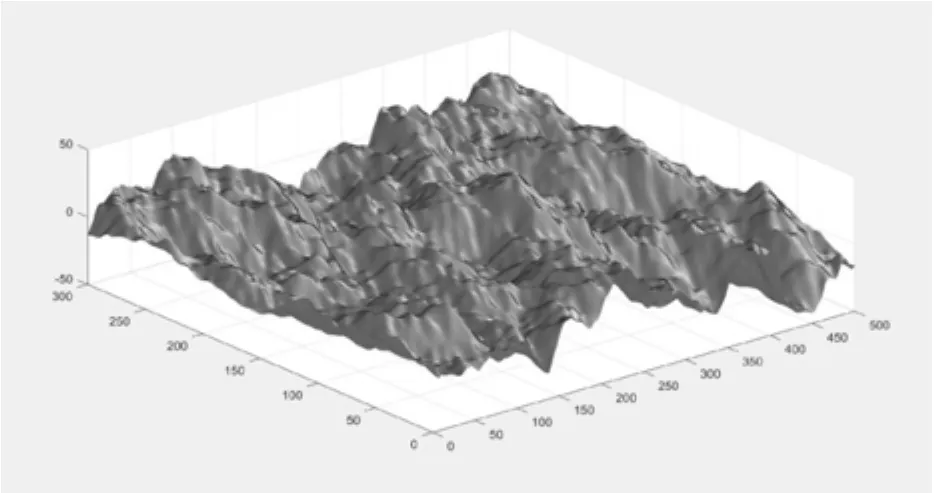
图1 崎岖的山地地形

图2 对应海面图

利用MATLAB可以读出换算系数ξ=24.28。

由以上可知，地面信号的反射能量损失明显大于海洋的损失。此外，地形越崎岖，能量损失越大。且粗糙地形的能量损失与波涛汹涌的海面能量损失相似，平缓地形的能量损失与平静的海面的能量损失相似。

当一艘船偏离某一信号发射站传送信号的最大范围时，它便不能从该发射站接收到有效的信号。这意味着这个特定信号的多条路径将无法被维护。

在之前的分析中，本文在平静海洋中建立了反射递归模型，计算出最大跳数。此处，穿过海洋的船就是接收点。将R作为目标函数，可得

我们可以看到，传输信号的强度必须大于信噪比。同时，信号传输必须在MUF以下。

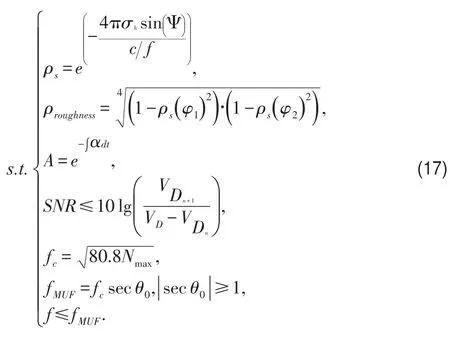
3 模型分析

3.1 模型优点

本文充分利用无线电波反射的原理及特性，直接结合其相关公式，对平静海面和汹涌海面两种不同的情况进行比较，能够直接得出两种情况下的信号强度差异与各个变量之间的关系。仅对反射过程中所损耗的能量进行分析，极大地简化了运算，避免了因参数过多而带来的干扰问题，同时又能够更直观地反映出无线电波信号经过平静海面和汹涌海面反射后能量损耗的差异。由于递推模型所得结果仅与前一状态结果相关，有效保证了运算结果的精确性和可靠性。故计算最大跳数时建立的递推模型能够更直观地反映出信号在当前反射过程中的能量损耗值与前一次反射过程中的能量损耗值之间的关系。同时，利用MATLAB数学软件随机画出崎岖地形图，并将其与不同海风级数下的汹涌海浪图比较，可以直观地分析出两者对无线电波信号的反射差异。同时，本文所建立的最优化模型能够很好地体现出所求量与各种约束条件之间的关系，使得计算的结果更加精确。

3.2 模型缺点

本文运用了过多原理、定理及相关公式，使得递推方程的参数较多，导致计算总量庞大，计算过程繁琐复杂，最终结果不易得出，对计算机依赖较大。同时，由于是利用MATLAB数学软件直接随机给出的地形图，因此其计算的结果不具有普遍性，可能并不适用于某些特殊类型的地形地势。除此之外，本文所建立的最优化模型是由递推模型改进而来，为保证结果的精确性引入了较多参数，且各参数间无法替代或消除，导致模型表达式十分繁琐，计算过程非常麻烦。