基于反余弦函数变换的优化GM(1,1)模型应用研究
2018-11-09,
,
(广东财经大学华商学院,广东 广州 511300;,湖南理工学院数学院,湖南 岳阳 414006)
0 引 言
邓聚龙教授提出的灰色系统理论[1]经过30多年的发展,已经在各个领域得到广泛应用,灰色预测模型具有建模简单、样本小、可检验等优点,人们用该方法解决了大量的实际问题。但是灰色GM(1,1)自身还存在一些缺陷,有时对事物的发展预测有些偏差,也有一定的局限性,所以近年来,很多学者从不同方面对该模型进行了改进,主要通过优化背景值和初始条件、改进灰导数、数据变换技术等途径对模型进行优化,并取得了良好效果,如文献[25]。
在文献[5]的基础上,结合反余弦变换和灰色预测模型新陈代谢思想对GM(1,1)模型进行优化,对文献[5]的数据继续计算,并与传统的GM(1,1)模型以及文献[5]模型结果进行对比,说明新的优化模型能使预测精度得到优化。
1 传统灰色预测模型的建立
基于灰色理论的GM(1,1)模型建立过程如下:
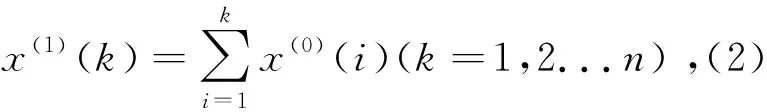
(3)建立关于x(1)的一阶白化微分方程:
(1)
并利用最小二乘法求解识别参数a和b,a为灰系数,b为作用量:[a,b]T=(BTB)-1BTYn
其中Yn=[x(0)(2),x(0)(3),...x(0)(n)]
(4)求出a和b后,可以求得方程(2.1)的时间响应序列(预测模型)
(2)
(5)还原模型为
(3)
2 优化灰色GM(1,1)模型的建立
2.1 原始数据序列的数据变换
文献[5]在满足数据变换的四原则“减小光滑比、调节级比压缩、保持序列凹性不变、还原误差不增大”下,构建了反余弦函数变换,证明了利用该函数变化对原始数据进行处理可以提高数据序列的光滑度。
2.2 初始值优化
初始值是影响GM(1,1)模型模拟与预测精度的一个重要因素,文献[2]引入新陈代谢思想优化GM(1,1) 模型,将初始条件由x(0)(1)用x(1)(k)的第个n分量x(1)(n)代替,能提高模型的预测精度。
2.3 优化后的GM(1,1)模型建立过程
(1)设原始序列a(0)=(a(0)(1),a(0)(2),…a(0)(n)),a(0)(k)>0,k=1,2...n,对其进行标准化处理,使其处于区间(0,1)内,得到新序列:
x(0)=(x(0)(1),x(0)(2),…x(0)(n)),
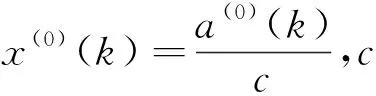
y(0)=(y(0)(1),y(0)(2),…y(0)(n)),
其中y(0)(k)=arccosx(0)(k),k=1,2...n
(2)对y(0)进行一次累加生成新的数据序列:
y(1)=(y(1)(1),y(1)(2),…y(1)(n)),
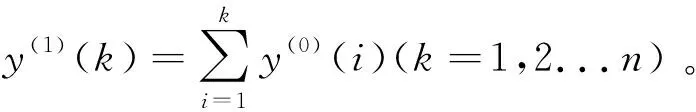
(3)对y(1)做紧邻均值生成序列:
z(1)=(z(1)(1),z(1)(2),…z(1)(n)),
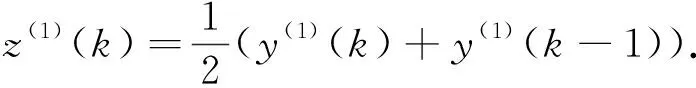
(4)依据GM(1,1)建模原理文献,建立对应的微分方程:
(4)
(5)令初始值y(1)(n),求解上述微分方程得到时间响应序列:
(k=1,2,...n)
(5)
(6)还原模型为:
(6)
(7)再由y(0)(k)=arccosx(0)(k),k=1,2...n得
x(0)(k)=arccosy(0)(k),k=1,2...n
(7)
3 实例应用
为了说明优化后的GM(1,1)预测精度更高,以文献[5]的数据建模见表1。
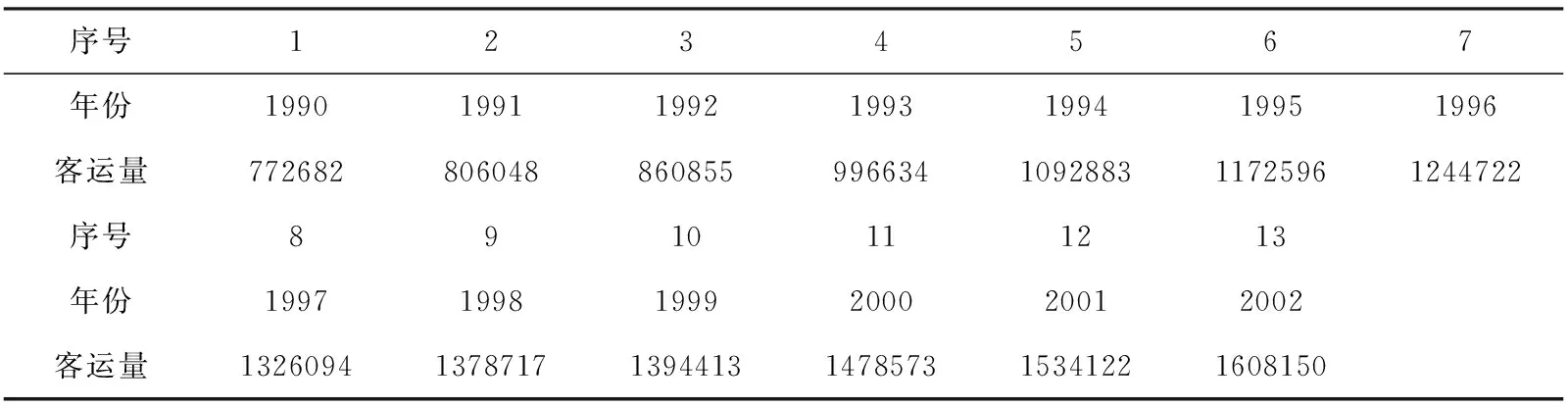
表1 1992-2002年我国客运量
文献[5]从理论上证明了用非零常数乘以原始序列进行GM(1,1)建模得到的预测值等于直接用原始序列进行建模的预测值乘以相同常数,由此说明对原始数据乘以一常数再进行建模不会改变模型的预测精度,所以将原始数据做如下标准化处理:
(8)
通过(8)将数据处理为:
(1.0990,1.0768,1.0398,0.9444,0.8726,0.8096,0.7492,0.6760,0.6249,0.6089)
一般来说,利用GM(1,1)模型进行预测,精度较高的仅仅是最近的几个数据,随着时间的推移和事物的发展,该模型的预测精度就会减弱,所以应用时,引入灰色理论中的新陈代谢思想,弥补这种不足。
运用表一中前10个数据,建立反余弦变换的GM(1,1)预测模型,后面3个数据用于模型的检验。用MATLAB计算得到反余弦变换的GM(1,1)预测模型为:
(9)
结合相应的数据变换得到预测值为:
结合灰色理论的新陈代谢思想,删除标准化后的第一个初始值1.0990,同时加上新得到的0.5486,得到预测值0.5017.再逐个预测,并做相应的数据还原处理,结果如表2所示。
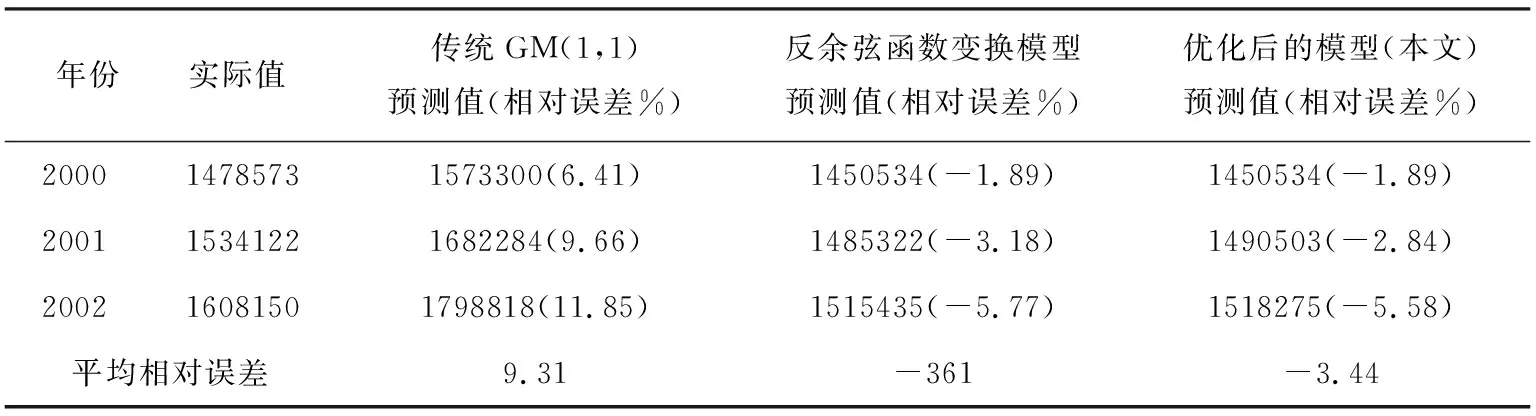
表2 三种不同模型预测结果及其相对误差比较
4 结 语
由三种模型预测平均相对误差可知,利用反余弦变换有效地改善了原始数据的光滑度,在反余弦函数变换的基础上,引入灰色理论中的新陈代谢思想后,提高了模型的预测精度,具有更加良好的实用性和有效性。
