具有部分缺失数据混合瑞利分布参数的估计
2018-11-09,,,
, , ,
(吉林师范大学数学学院,吉林 四平 136000)
0 引 言
瑞利分布是统计学中一种重要的连续概率分布,当今有许多学者对瑞利分布进行统计研究,Abbas Pak等[1]在Estimation of System Reliability under Bivariate Rayleigh Distribution中研究了二元瑞利分布的可靠性估计问题。杨慧超等[2]对缺失部分数据的两个Rayleigh分布参数进行矩估计与检验。在对观测数据做统计分析时,常会碰到数据缺失的情况,田霆等[3]对定时截尾缺失数据下指数分布进行统计推断。探究当缺失部分数据时混合瑞利分布总体的参数估计问题,利用矩估计的方法求出参数的矩估计,给出其渐近正态性,并且随机模拟的结果也表明了参数估计是正确的。
1 矩估计及其渐近性质
假设有四个混合瑞利分布[1],其密度函数分别为
首先设定为常数0.2,(1-q)为常数0.8,然后分别取δi>0(i=1,2)为两个总体的未知参数,ηi(i=1,2)为另两个总体的未知参数,接着依次对混合瑞利分布独立观测n次,从每个分布总体抽取样本进行观测时,记1-p为缺失样本时的概率。Xi是第一个总体的第i个样本观测值,i=1,2,…,n,且(Xi,θi)是第一个混合瑞利分布第i个总体观测值,假设没有观测到第i个样本记θi=0,如果不是这样记θi=1,Yi是第二个总体的第i个样本观测值,i=1,2,…,n,且(Yi,βi)为第二个混合瑞利分布总体的第i个总体观测值,若没有观测到第i个样本记βi=0,如果不是这样记βi=1。
下面对参数δ1,δ2进行矩估计。根据(Xi,θi),i=1,2,…,n,可以建立如下的矩估计方程[2]
其中
解出方程得
同理可得得到另一组观测值(Yi,βi)后,得到η1,η2的矩估计
对如上参数δi(i=0,1),ηi(=0,1)的矩估计,下证相合性以及渐近正态性[3]。
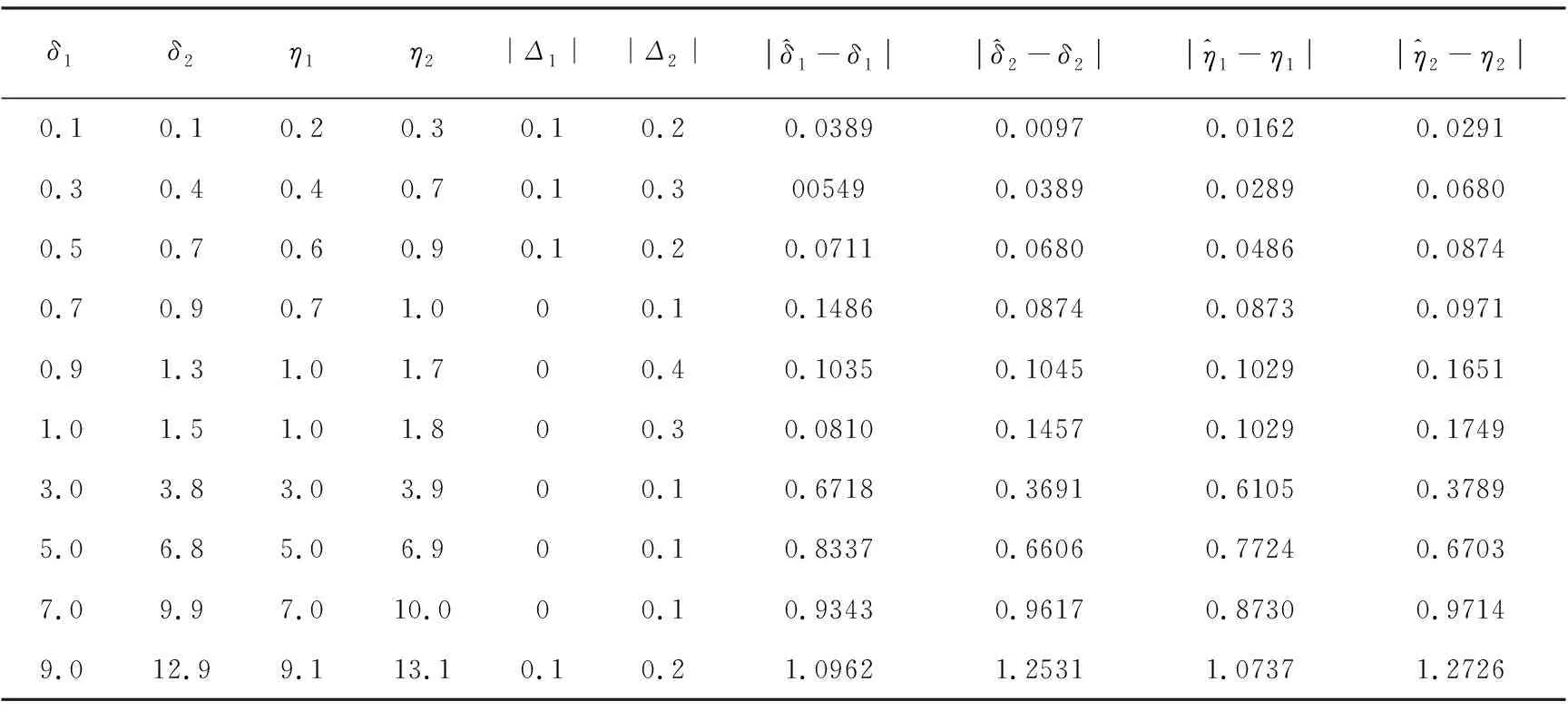
证明: 因为{Xi,θi,1 并且 同理得出 因此得出 令∑=E(W1-EW1)(W1-EW1)T,于是根据多元中心极限定理得出 令 于是得出 根据引理1 并且 同理令 根据引理1 并且 同理证出 表1 随机模拟结果 通过上述得出当缺失部分数据时,混合瑞利分布的参数矩估计具有渐近正态性,由矩估计的方法得到的随机模拟结果见表1,参数估计值的误差也都相对很小,充分表明矩估计的方法具有稳健性。


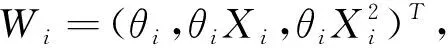

2 随机模拟