均匀剪切流中粒子无规行走的分子动力学模拟研究

， ,

(北京航空航天大学a.航空科学与工程学院;b.航空科学与工程学院；c.国家计算流体力学重点实验室， 北京 100191)

0 引 言

对于模拟真实的稀薄气体分子与真实物面的相互作用[1]，要选择一个计算区域。为保证流动充分发展，这个计算区域至少要大于分子平均自由程[2]。分子平均自由程与分子扩散系数成正比，而扩散系数又与分子无规行走距离相关，但是在均匀剪切率情况下，平均自由程与剪切率是什么关系还不是很清处，因此要研究平均自由程和剪切率的关系，通过分子动力学模拟的方法[3]来研究不同均匀剪切率Couette流与分子无规行走曲线的斜率的关系，这样可以为该计算区域大小的选择提供一个参考，节省计算量。

1 模拟细节

1.1 基本参数设定

选用一般力场中最常见的非键结形式为Lennard-Jones(LJ)势能[4]。此势能又称为12-6势，其数学表达式为：

(1)

σ与ε为势参数，令σ为无量纲特征长度，并对其他长度变量进行无量纲化，r为两粒子之间的距离。

模拟的物理模型如下如图(1)所示：

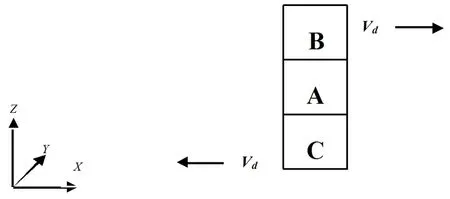
图1 分子动力模拟Couette流的模型

A盒子中粒子是所要计算的一系列粒子，而B盒子与C盒子中的粒子是A盒子中的镜像粒子，但是这并不会维持一个稳定的Couette流动，为了获得沿着z轴方向的速度梯度，选择让B盒子沿着x轴正方向开始以速度Vd运动，而C盒子沿着z轴负方向具有一个Vd的运动。在B盒子与C盒子的拖动之下，形成了具有一定剪切率的Couette流动。剪切率γ=Vd/Lz,其中Lz为A盒子的z轴高度。选择Lz为40。

分子的初始位置按照面心立方(FCC)晶体结构布置，粒子总数为2048个恒定。整个模拟的A盒子的尺寸大小为40*40*40。每个粒子初始速度给定。整个系统的温度是不变的。采用蛙跳算法来计算粒子的加速度，速度和位置时。选用Andersen的定温计算法[5]，运用常用的分子热运动公式Ct=3×k×T/2，其中εt为分子热运动平动动能，k为波尔茨曼常数，调节每一步的系统温度，使其保持定值。初始系统温度T的无量纲值为0.75。

为了保持粒子数密度守恒，应用改进的周期性边界条件[6]。而与该文章不同的是，没有忽略粒子x方向的受力。

2 模拟结果与讨论

2.1 无规行走曲线及斜率

y与z方向无规行走，可以通过这两个方向的热运动速度定义。当粒子初始位置布置好之后，要给粒子一定的热运动速度，再给予分子一有梯度的宏观速度。让其运动达到稳定后，再来计算分子的无规行走曲线。研究选用粒子宏观的运动速度为x轴正方向的。

在y轴和z轴方向，每个粒子在某一个时刻的无规行走位移用以下公式计算：

(2)

其中，X1为在某一时刻某一粒子的位置，X2为该粒子初始时刻的位置。N为粒子总数。无规行走是所有粒子的运动位移平方相加取平均值。

画出三个典型的速度梯度无规行走曲线与时间关系图。由于y、z方向无规行走曲线类似，都为直线，现只作出z方向无规行走曲线。如下图所示为运行106步的三种不同速度梯度Couette流动的z方向无规行走曲线。

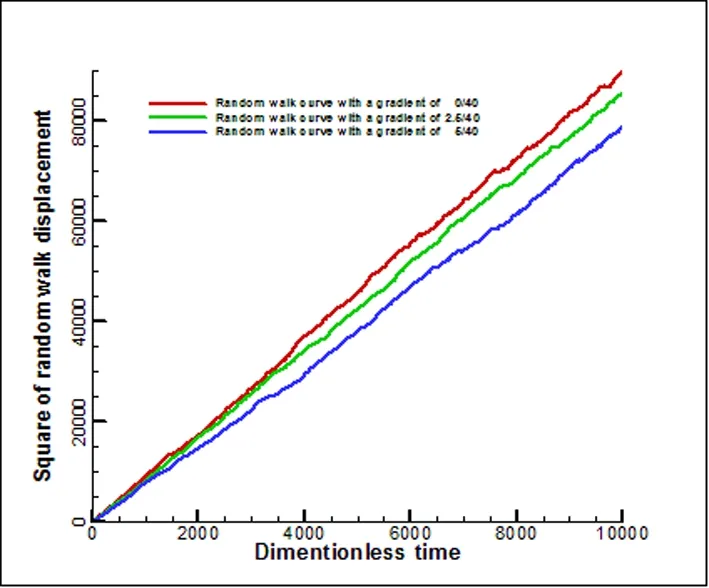
图2 无规行走位移的方均值与时间的关系

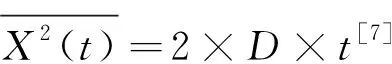
利用最小二乘法拟合不同速度梯度下的无规行走曲线。

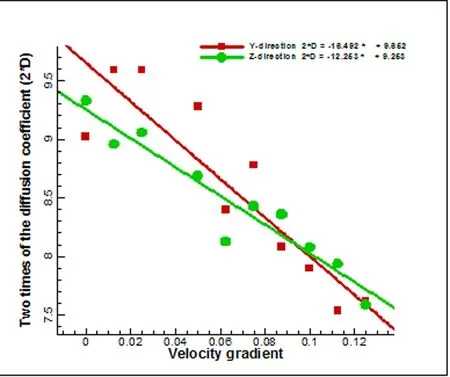
图3 无规行走曲线斜率与速度梯度的关系

从图(3)中可以看出，y、z方向的无规行走曲线斜率与速度梯度近似呈直线关系。随着速度梯度的增加，y、z方向无规行走曲线斜率线性减小。无规行走曲线斜率亦即上文提到的2D，D为扩散系数。这是因为粒子在运动时，因为速度梯度的增大，粒子从速度较低层向速度较高层运动时，速度较高层粒子运动速度快，沿着x方向单位时间扫掠过的空间增大，更有可能与扩散到此层的低速层粒子发生碰撞；反之，高速层粒子扩散到低速度层，沿着x方向单位时间扫掠的空间更大，更有可能与低速层的粒子发生碰撞。这样就会导致粒子在y、z两个方向碰撞增多，所以平均位移减小。而同一个剪切率的y轴无规行走曲线与z轴无规行走曲线斜率的差别不大。因为调温的作用，y方向与z方向的速度保持原来的量级不变，还是原来的热运动速度，并且二者都是随机的粒子向y轴运动就会以同样的概率向着z轴运动，二者是协调相关的。由于空间的对称性，可以证明没有速度梯度的时候，稀薄气体具有各项同性。而有速度梯度时这种各向同性趋势被打破，稀薄气体具有各项异性。从图中即可看出随着剪切率的增加，y方向无规行走曲线斜率比z方向的下降的更快。至于为什么会出现y方向无规行走曲线斜率比z方向的下降的更快的结果，有待进一步去研究探索。

这样来说，粒子y轴和z轴粒子仍然是以热运动速度在运动，而x轴的无规行走貌似不是很容易定义。可以从测量粒子无规行走位移的角度来定义无规行走速度，故需要在剪切流动中建立速度运动坐标系。本文定义的x方向无规行走速度是相当于每个粒子每个时刻x轴方向的绝对速度在初始宏观速度坐标系下的相对速度。即公式(3)：

定义无规行走速度Vb(式3)为初始速度V0下的相对速度

Vb=Va-V0

(3)

Vb表示粒子在此时的无规行走速度，Va为粒子的绝度速度,V0为粒子在初始时刻的x方向宏观运动运动速度。实际上粒子的无规行走速度相当绝对速度在初始宏观速度坐标系下的相对速度。

从速度梯度0/40,到速度梯度5/40，每增加0.5/40的速度梯度计算无规行走，如下图所示为运行106步的速度梯度γ=1/40的Couette流动的x方向无规行走曲线。

图(4)B即是图(4)A横纵坐标轴同时取对数的结果。从图(4)A中可以看出，x方向无规行走曲线斜率随着速度梯度的增大而增大，因为定义的x方向无规行走速度是相当绝对速度在初始宏观速度坐标系下的相对速度，当粒子运动到宏观速度更高的流层时，由于碰撞，它将获得平均速度增量Δv=γz。这样会导致x方向无规行走速度变大，因此无规行走位移增加。图(4)B为图(4)A在横纵坐标轴取对数之后的结果。可以看出图(4)B的为两段直线。第一段直线的原因是由于流动没有充分发展，碰撞次数不够多。位移与时间成线性关系，因此三种不同速度梯度的曲线严格重合,而且第一段直线的运算时间只是在104的量级,第二段直线是文中主要研究的,对第二段直线进行最小二乘拟合，拟合出气体分子无规行走位移的方均值与时间t的关系是：

(4)

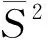
(5)

(6)

由于z方向具有速度梯度，当粒子从x方向宏观速度较低层向x方向较高层运动时，由于粒子之间的相互碰撞，假定粒子获得了Δv=γz的速度，由此式带入得到(6)：

(7)

(8)

将(8)式两边平方得到

(9)

此式中的γ2* 2 *Dz即为上文中的系数a，可见它并不单单与扩散系数有关。

在不同速度梯度下计算a的值，用tecplot作图并作出最佳拟合曲线：

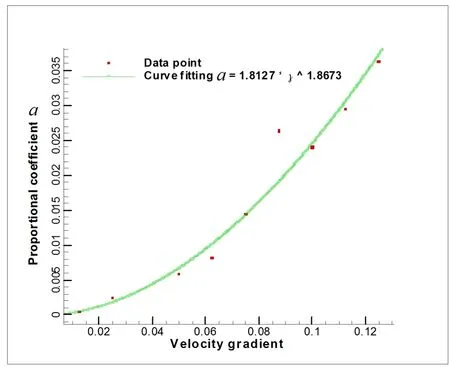
图5 无规行走曲线斜率与速度梯度的关系

从图(5)中可以看出，随着速度梯度的增大，比例系数a值呈现非线性增加。至于为什么会出现这样的结果有待进一步去探索研究。

3 结 论

通过分子动力学模拟的方法来研究不同均匀剪切流与分子无规行走曲线的斜率的关系。应用分子动力学的模拟方法，模拟出了均匀剪切流，利用分子无规行走曲线计算公式，计算出不同均匀剪切流的无规行走曲线，计算无规行走拟合曲线斜率。计算结果表明，在相同时间条件下，速度梯度越大，x轴方向无规行走曲线斜率增大，y轴z轴两个方向的无规行走曲线斜率越小，速度梯度越大对无规行走位移压缩越严重。而同一剪切率下的y轴无规行走曲线与z轴无规行走曲线斜率的差别不大。在x轴方向分子无规行走位移的方均值与时间t的三次方成正比，比例系数a与分子扩算系数Dz以及速度梯度γ有关，并随着速度梯度增大呈现非线性趋势；在y轴、z轴方向分子无规行走的方均值与时间t成正比，其比例系数即扩散系数的二倍即2*D随着速度梯度增加而线性减小。