耦合电感式高增益Boost变换器分析研究

， ，

1.(安徽新华学院，安徽 合肥 230000；2.安徽省煤炭科学研究院，安徽 合肥 230001)

0 引 言

近年来，新能源开发和利用备受关注。如在光伏和风力发电系统中，因其输出电压等级较低，不能满足需求，需直流变换器的参与来提高电压等级。

国内外专家提出很多高升压比和高效率的拓扑结构。文献[1]提出将串并联二极管电容网络与传统Boost电路结合，相同占空比下可提高升压比，但占空比范围有一定限制，且开关管电压、电流应力较大。文献[2-3]提出改进二次型Boost变换器拓扑，在电流连续模式下升压能力有所提升，但占空比增大，优势不明显。文献[4]提出利用开关电感的Boost变换器拓扑，提高了电压增益，但对开关管及二极管的电压应力减少不明显，且增加了原器件数量，电路可靠性差。

耦合电感式高增益直流变换器，通过改变占空比来改变输出电压，还可通过调节线圈匝比来提高升压比。同时主开关管的电压、电流应力大大减少，从而极大地减少了开关损耗。

1 电路分析

1.1 工作原理

耦合电感型高增益直流变换器拓扑图如图1所示。用耦合电感替换普通电感，由于耦合电感可以等效为原、副边匝比为N(n1/n2)的理想变压器与激磁电感Lm并联后再与漏感Lk相串联，其中Lk包含原边漏感及副边折算到原边的等效漏感。为了便于分析，将变换器进行等效变换，等效电路图如图2所示。下面将根据等效电路图分析其工作原理，分析之前需做出如下假设：1)所有器件均为理想器件，不考虑寄生参数的影响，但开关管的寄生电容Cs存在；2)电容C足够大；3)在考虑漏感时，耦合系数k=Lm/(Lm+Lk)，耦合电感的匝比N=Ns:Np。

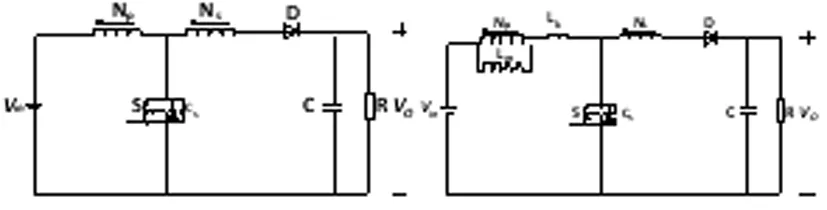
图1 主电路 图2 等效电路

(1)理想情况，不考虑漏感Lk

当变换器稳态工作时，在一个开关周期T内共有两个工作模态。

模态Ⅰ：当开关管S导通时，工作电流的流通路径如图3所示。在这一阶段，电源电压Vin对耦合电感的原边线圈进行充电，原边线圈存储能量。在开关管关断之前，这一工作模态结束。

模态Ⅱ：当开关管S关断时，工作电流的流通路径如图4所示。在这一阶段，开关管关断的瞬间，耦合电感原边的部分能量转移到副边线圈上。同时，电源电压、原边线圈电压、副边线圈电压共同向电容C和负载R充电，原边线圈存储的能量释放完毕，这一工作模态结束。

图3 导通时电流流通路径 图4 关断时电流流通路径

(2)实际情况，考虑漏感Lk

当考虑漏感时，该变换器就不止工作在两个模态，而是三个模态，其中在开关管断开的期间内就有两个模态，包括漏感的能量释放到寄生电容Cs上、电源电压与耦合电感的电压向负载和电容C释放能量。

模态Ⅰ：当开关管S导通时，工作电流的流通路径如图5所示。在这一阶段，电源电压Vin对耦合电感的原边线圈进行充电，原边线圈存储能量。在开关管关断之前，这一工作模态结束。

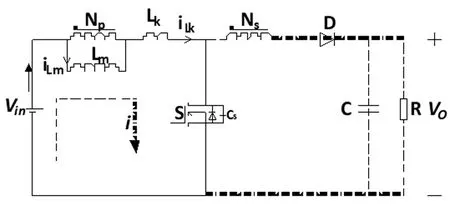
图5 开关管导通时电流流通路径

模态Ⅱ：当开关管S关断时，工作电流的流通路径如图6所示。在这一阶段，由于漏感的存在，电流方向不能突变，且漏感的能量释放到开关管的寄生电容Cs上，对电容Cs进行充电，由于漏感的值很小，其储存的能量也有限，所以这一过程持续的时间非常短，当输出二极管开始导通时，这一工作模态结束。

模态Ⅲ：开关管S继续关断，工作电流的流通路径如图7所示。在这一阶段，输出二极管D开始导通，耦合电感原边的部分能量转移到副边线圈上。同时，电源电压、原边线圈电压、副边线圈电压共同向电容C和负载R充电，原边线圈存储的能量释放完毕，这一工作模态结束。

图6 关断瞬间电流流通路径 图7 关断后电流流通路径

1.2 性能分析

(1)理想情况，不考虑漏感存在

在图5中，激磁电感Lm在开关管S导通时存储能量，在S关断时释放能量。由伏秒平衡原则可以推导出变换器的电压增益。在S导通时，即模态Ⅰ，根据KVL定律可得，激磁电感两端的电压为VmI。当S关断时，即模态Ⅱ，根据KVL定律可得，激磁电感两端的电压为VmII。

(1)

(2)

由式(2)得：

(3)

在一个开关周期T内，根据伏秒平衡原则，有：

(4)

即：

(5)

由式(5)可得电压增益M为：

(6)

接下来分析开关管S和输出二极管D的电压应力VT和VD。在S关断时，根据KVL定律得：

Vo-Vin=Vp+Vs

(7)

(8)

VT=Vin+Vp

(9)

由式(7)、(8)和(9)得：

(10)

在S导通时，根据KVL定律得：

Vin=Vp

(11)

Vs=NVp

(12)

VD=Vs+Vo

(13)

由式(11)、(12)和(13)得：

VD=NVin+Vo

(14)

在理想情况下，耦合电感变换器的电压增益与占空比和匝比之间的关系如图8所示。当N=0时，电压增益即为传统Boost变换器的电压增益。从图中可以看出，当匝比N不变时，变换器的电压增益是随着占空比的增大而增大；当占空比D不变时，变换器的电压增益是随着匝比的增大而增大。因此，只要匝比大于0，该变换器的电压增益就高于传统Boost变换器，而且在选择了适当的占空比下，可以有效避免占空比工作在极限值下，大大减小了开关管的开关损耗，提高了变换器效率。

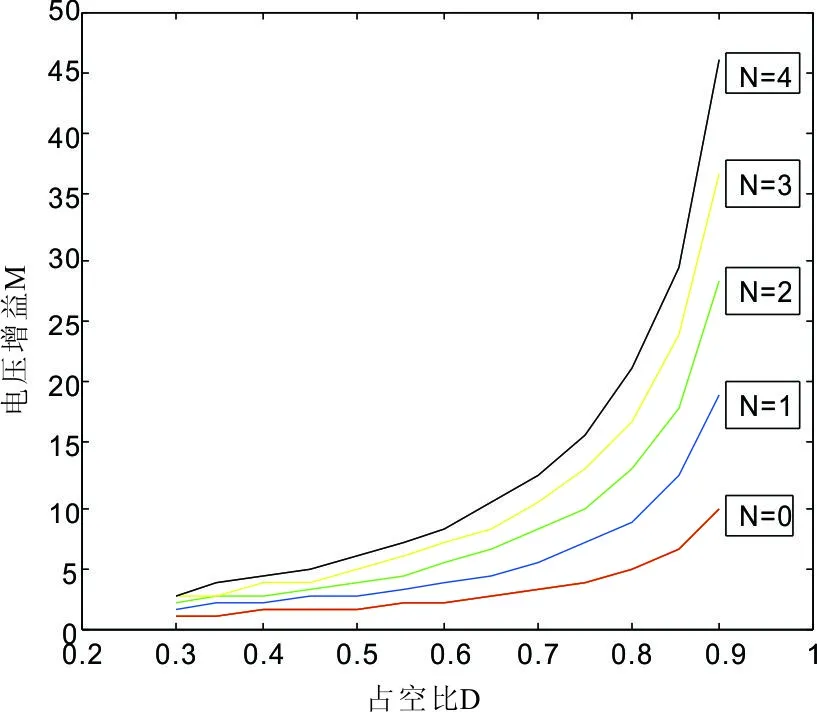
图8 电压增益与占空比和匝比的关系

(2)实际情况，考虑漏感存在

当存在漏感时，在开关管关断的瞬间，输出二极管并没有受正偏电压而导通，此时是漏感所储存的能量要向开关管的寄生电容进行释放，向寄生电容Cs进行充电。对于一个开关周期来说，这一过程所经历的时间很短，在分析变换器的性能时是可以忽略的。在分析变换器的电压增益和开关管的电压应力之前，需要说明一下，在该变换器中，激磁电感Lm两端的电压和漏感两端的电压之比等于其电感值之比，即

(15)

曾假设k=Lm/(Lm+Lk)，则有

(16)

当开关S导通时，即模态Ⅰ，根据KVL定律：

(17)

化简得：

(18)

当开关S关断时，即模态Ⅲ，根据KVL定律

(19)

又Vs=NVm，化简得

(20)

一个开关周期T内，根据伏秒平衡原则，有

(21)

即

(22)

由式(22)可得电压增益M为

(23)

接下来分析开关管S和输出二极管D的电压应力VT和VD。在S关断时，根据KVL定律：

Vo-Vin=Vp+Vs+Vk

(24)

(25)

VT=Vin+Vp+Vk

(26)

由式(24)、(25)和(26)得

(27)

在S导通时，根据KVL定律得

Vin=Vp+Vk

(28)

(29)

VD=Vs+Vo

(30)

由式(28)、(29)和(30)得

VD=kNVin+Vo

(31)

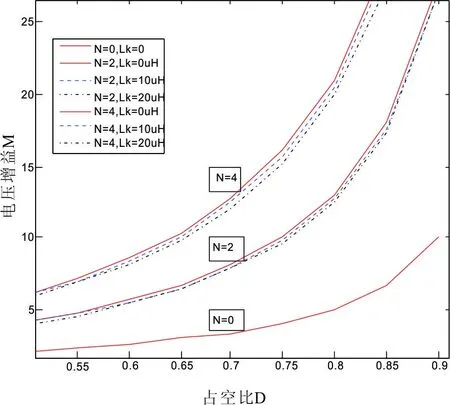
图9 电压增益与占空比和匝比的关系

在实际情况下，当有漏感存在时，耦合电感变换器的电压增益与占空比和匝比间的关系如图9所示。从图中可以看出，当匝比N不变时，变换器的升压比是随着占空比的增大而增大；当占空比D不变时，变换器的升压比是随着匝比的增大而增大。漏感对变换器的电压增益影响较小，且当匝比N和占空比D均不变时，变换器的电压增益随着耦合电感漏感值的增大而降低。

2 仿真结果及分析

为了验证所提变换器的工作原理和性能分析，基于PLECS软件搭建模型进行仿真分析。参数为：输入电压50V；理想变压器的匝比N=2；激磁电感Lm为300uH；输出电容C为470uF；负载电阻R为400Ω；考虑漏感时，漏感Lk为10uH。

图10 输出电压波形

(1)不考虑漏感

输出电压波形如图10所示，开关器件电压应力如图11所示，输入输出电流波形如图12所示。在进行理论分析时，开关管的电压应力表达式为VT=Vo+NVin/1+N，将Vin=50V、Vo=380V、N=2代入得，VT=160V。易知上述仿真的结果为160.375V，误差为ess1=(160.375-160)/160=0.2%，误差小于1%，仿真结果与理论分析一致。输出二极管的电压应力表达式为VD=NVin+Vo，将Vin=50V、Vo=380V、N=2代入得，VD=480V。仿真结果为479.159V，误差为ess2=(480-479.159)/480=0.17%，误差小于1%，仿真结果与理论分析一致。

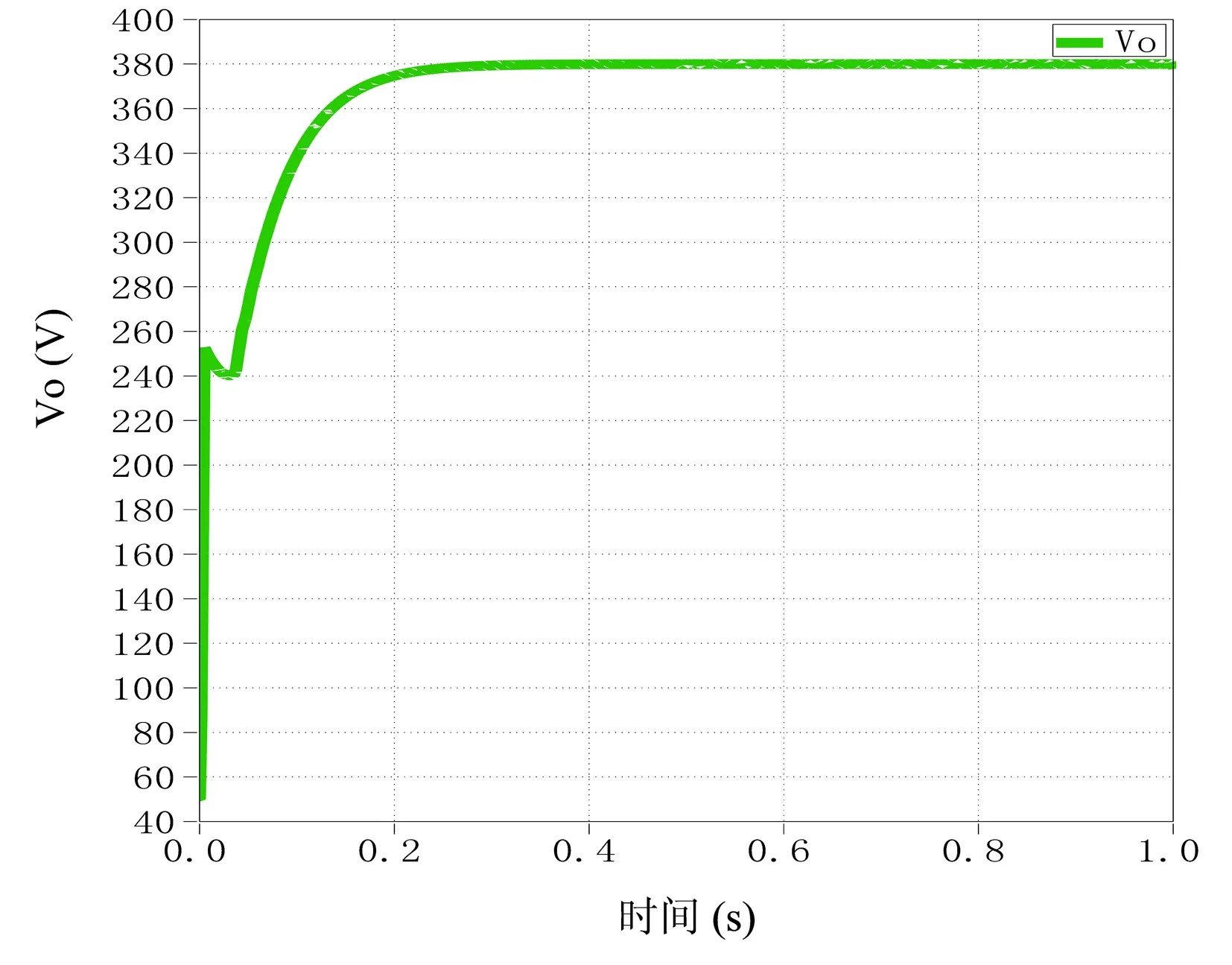
图13 输出电压波形

图14 开关管及二极管电压应力

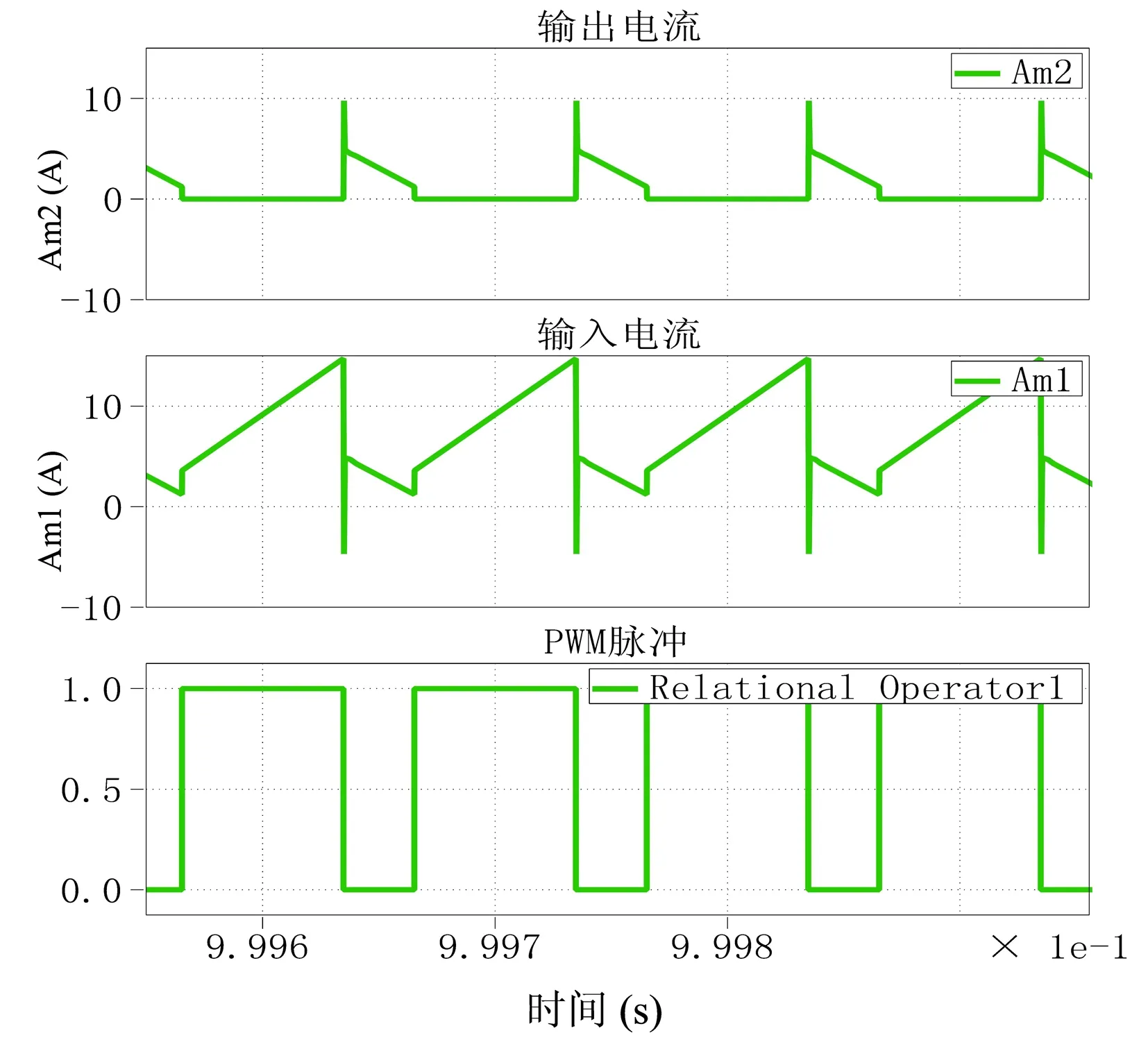
图15 输入电流及输出电流

(2)考虑漏感

输出电压波形如图13所示，开关器件电压应力如图14所示，输入输出电流波形如图15所示。

在考虑漏感时，激磁电感的Lm的值为300uH，漏感Lk的值为10uH。又k=Lm/(Lm+Lk)，则k=0.968。在进行理论分析时，开关管的电压应力表达式为VT=(Vo+kNVin)/(11+kN)，得VT=162.4V。上述仿真的结果为161.192V，误差为ess3=(162.4-161.192)/162.4=0.7%，误差小于1%，仿真结果与理论分析一致。输出二极管D的电压应力表达式为VD=kNVin+Vo，将Vin=50V、Vo=380V、N=2代入得，VD=476.8V。仿真结果为475.958V，误差为ess4=(476.8-475.958)/476.8=0.18%，误差小于1%，仿真结果与理论分析一致。

综上所述，仿真结果与理论分析相一致。耦合电感型高增益直流变换器，相比于传统升压变换器(Boost变换器)，大大提高了电压增益，同时，开关管的电压应力也大大降低。因此，极大地降低了开关管的开关损耗，提高了变换器效率。

3 结 论

在传统Boost变换器的基础上，研究了一种耦合电感型的高增益直流变换器。文章首先从考虑漏感和不考虑漏感两个方面，着重分析了该变换器拓扑的工作原理，从分析的结果可以看出，该变换器相对于传统变换器，不仅能够通过改变占空比来调节电压增益，最重要的是可以通过改变耦合电感匝比来调节电压增益，这样也有效避免了开关管工作在极限占空比的情况下。同时，通过理论分析可知，主开关管的电压应力也大大减小，从而减少了开关损耗，一定程度提高了变换器效率。然后，基于PLECS仿真平台，搭建仿真模型进行仿真，很好地验证了理论分析的正确性。